1 引言

　　短期负荷预测是电网经济运行的前提和基础。准确的负荷预测结果，对电力系统安全可靠运行具有重要意义。许多学者对此进行了深入研究，并及时地将数学上的最新成果应用到负荷预测领域中去，使预测水平得到提高，小波网络便是基于小波分析理论而构成的人工神经网络模型，它同时具备了小波变换良好的时频局部化性质和神经网络的学习能力，它既可以在网络结构的确定上有一定的理论指导，又具有神经网络的许多优秀特性，并且网络的训练是对特定的凸函数的优化过程，学习速度比一般网络要快[3]。
　　研究表明，小波网络比神经网络使用的基函数单元更少，具有更快的收敛速度和更高的精度，然而小波网络有两个明显的不足：在多维输入情况下，学习所用小波基数目过多，其次是随着网络输入维数的增大，使得小波网络的收敛速度大大下降，即不能够解决所谓的“维数灾”问题[5]。由于影响电力系统短期负荷预测的因素诸多，本身也是一个多维输入问题，基于此，本文提出了一种将小波网络和模糊神经网络相结合的短期负荷预测的新方法，利用一组模糊规则将小波网络分为若干小波子网络，每条模糊规则前提部分将输入样本空间划分为一个局部子空间，其结论部分则对应某一特定尺度下的小波子网络，不同尺度下的小波子网络用于捕捉信号的各种不同特性，将其进行线性组合来逼近信号。它在保证选择一定数量的小波基函数下，由隶属度函数和小波子网络的输出来精确确定整个网络的输出，使网络到达最佳逼近，同时简化了网络的结构，避免了小波网络的“维数灾”问题，提高了计算效率。实践证明该方法具有较高的精度和很强的泛化能力。

2 小波网络
　　 对于输入X=[x1,x2,...xq] ，定义其多维小波母函数为[5]：
　
    由小波分析理论知，任一能量有限的信号都有如下离散小波分解形式[2]：
　
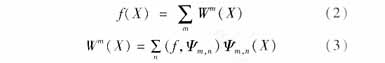
其中：Wm（X）为尺度层m上的小波分量，n是尺度层m上的小波函数的平移因子。
　　从式（2）、（3）中不难看出任一信号f(X)都可以分解成在不同尺度层上小波分量的线性组合，这正是我们提出FWN(模糊小波网络)的出发点。
　　从理论上来说，信号的小波展开式的基有无穷多个，而在分析电力负荷频谱特性时发现，负荷信号的变化过程具有连续频谱的特性[4]，负荷预测仅涉及一个频带，故只需选择最能代表信号信息的主频段来逼近信号。因此在一定精度要求下总可以截取有限小波函数作为基函数，得：
　
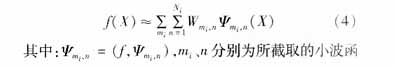
数的尺度及平移因子。这样就可以用一个以小波函数作为激活函数、wmi,n作为从隐含层到输出层的权值的小波神经网络来表示信号f(X)∈L2R。在本文所采用的FWN中，为了避免多维小波网络的“维数灾”问题，采用了若干小波子网络，每一小波子网络表示在同一尺度层上的小波分量的线性组合，从而使复杂问题简单化，达到分而治之，结合模糊神经网络将各小波子网络进行线性组合，来逼近信号f(X)，一小波子网络的结构如下图1。

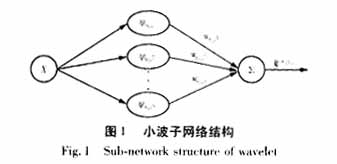
　　由小波理论的多分辨率分析可知，粗尺度层上的小波网络用于捕获信号的全局信息，而较细尺度层上的小波网络用于捕捉信号的各种局部信息，使FWN网络具有明确的物理意义，每一小波子网络的规模大大简化，易于进行训练，提高了计算效率的同时也提高了预测精度。

3 模糊小波网络结构
　　本文采用由Takigi-Sugeno改进的模糊推理方法[5]，假定模糊系统有q个输入，单个输出其模糊规则有着如下形式：
 
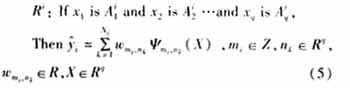
其中，Ri表示第i(1≤i≤c)条模糊规则；Xj(1≤j≤q)为输入集X中的第个变量；Ni表示第i条模糊规则中选用的小波基总数；nk=[n1k,n2k,...,nqk]为平移因子；而则是第i条模糊规则的输出，其值为具有相同尺度因子2mi小波基的线性组合，本文用一个小波子网络表示；模糊子Aij集用隶属度函数 
  
    由模糊推理层得到每条模糊规则对于输入X的适用度μi(X)，实现归一算法得到其激活度，它主要是决定了每个小波子网络的输出在整个网络输出中所占的比重：
 
 
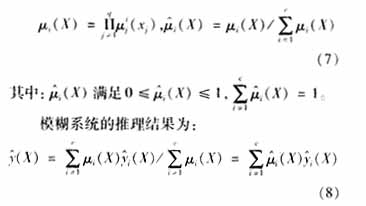
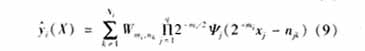
    在改进的Takigi-Sugeno模糊神经网络和小波网络的基础上，式(5)－(8)所描述的FWN可以用一个多层网络来实现，如上图2中所示.

    该FWN由常规的四层模糊神经网络组成，分别为：输入层、隶属度函数生成层、推理层及反模糊化层，各层神经元数目分别为q，q×c，和c+1，所以一旦确定输入个数和模糊规则数，模糊小波网络的结构也就确定了，WNNi表示第i个小波子网络。在隶属度函数生成层中所采用的激活函数是式(6)中给出的高斯型隶属度函数。
    本文中采用的FWN模型与常规的模糊神经网络模型最大的区别就在于反模糊化层的不同，在模糊神经网络中只能对信号进行局部化逼近，而FWN中则采用了一系列小波子网络，它既能对信号进行全局逼近，也能进行局部逼近，而且对于确定模糊规则数有合理的依据，正因为此，FWN具有更好的信号逼近能力和更强的适应力。

4 模糊小波网络的学习算法
    给定L个训练样本对，Xl(l=1,2,...,L)表示第l个训练样本的输入，分别表示网络的实际输出和目标输出。求解FWN的参数采用使之间误差最小的BP算法，其流程如下：
  
 
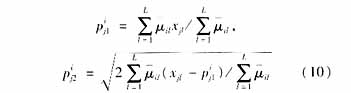
    （3）读入训练样本对，计算网络输出，并计算训练误差：若满足精度要求，则跳转到（5），否则继续；
 
 
式中:η、a分别是学习速率和惯性常数。跳转至（3）.
    （5）获得网络参数训练过程结束。

5 算例分析
    为了验证方法的可行性和有效性，本文以某市电力系统实际历史负荷为例，用上述FWN模型进行短期负荷预测仿真。
    选取模型的输入量有22个，分别是待测日和待测日前一天的最高温度、最低温度、湿度和天气状况；待测日前一天的最大、最小及平均负荷；待测日前一天及前两天分别以预测时段为中心取五个负荷值，待测日前一周预测时段的负荷值。输出量有1个为待测日某时段的负荷值，本文采取的是逐点预测。利用待测日前六周的历史数据来训练网络。其中学习速率η＝0.25，惯性常数a＝0.6，学习误差E=0.0005%，尺度mi取6个值(mi=-1,0,1,2,3,4)，分别为－1到4，也即是有6条模糊规则。为了比较模型优劣，在选择相同的训练模式、学习速率和惯性常量下，采用人工神经网络来模型进行负荷预测，取预报日为2001年6月7日(正常日)，其预测结果如表1，同时还给出了负荷变化最大、温度和天气状况变化最剧烈几日的预测结果，如表2。

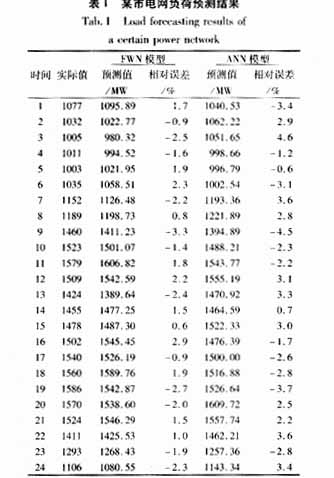
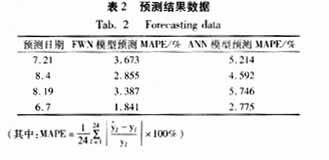
    从预测结果我们可以看出，基于模糊小波网络的负荷预测精度得到显著提高，同时也证明这种方法是完全可行的。从表1中还可以发现模糊小波网络的预测相对误差变化很均匀，表明其泛化能力比神经网络大有提高。从表2中可以看出模糊小波网络能够更好地拟合负荷与天气因素之间的密切关系，进行更加可靠的预测。

6 结论
    由于电力系统日益庞大，各个方面因素的影响使得负荷变化的不确定性增加，这也加大了负荷预测的难度。近年来，许多电力工作者也提出了各种负荷预测模型，其中小波网络便是近年来结合小波变换与人工神经网络思想而形成的一种数学建模方法，研究表明小波网络的预测精度和计算速度比普通神经网络有较大提高，但是小波网络的缺点是一般只适合低维情况，而且为了达到更高的预测精度需要较多的小波函数，为了有效的处理高维问题的不足，本文提出了一种新颖的基于模糊小波网络的短期负荷预测模型，这种FWN模型将小波网络和模糊神经网络有机结合起来，利用一组模糊规则，采用一组小波子网络的结构模型，使得小波子网络的隐层规模大大降低，避免了小波网络的“维数灾”问题，提高了运算效率，通过同时调整小波函数的位移因子和隶属度函数的形状，可以达到全局最优的拟合效果，从而有效地提高了预测精度。通过大量仿真计算表明，该方法是可行且有效的，同时本文为小波网络在电力系统负荷预测中的应用做出了进一步探索研究。