0 引 言

　　开关变换器是典型的强非线性系统，因此，其电路动态运行解析的分析方法较复杂。为解决工程上遇到的一些开关变换器的设计问题，必须对其进行动态建模。开关变换器的建模方法一般可分为两大类:一类称为数字仿真法;另一类称为解析建模仿真法。前者的准确度和精确度都高，但物理概念不明了，对工程设计指导意义不大。工程上较常用的是解析建模法中的状态空间平均法和电路平均法。电路平均法主要有:

　　三端开关器件模型法、时间平均等效电路法、能量守恒法。在前面的各种建模方法中，都没有考虑寄生参数的影响，不利于提高模型精度。而能量守恒平均法考虑了变换器寄生参数的影响且物理意义直观明确，克服了以往技术的不足。

　　本文介绍了能量守恒法的原理、建模步骤和仿真分析。最后针对Buck 型DC-DC 变换器利用能量守恒法建立的模型对其进行小信号动态分析。

　　1  能量守恒平均模型

　　下面以Buck 变换器为例进行说明，Buck 变换器如图1 所示，开关管S 的开关周期Ts ，TON为导通时间，Toff为关断时间，占空比为Du 。图2 是考虑寄生参数的变换器的等效电路，功率开关管等效为理想开关和开通电阻r DC的串联，二极管等效为理想开关、正向压降UF 、正向电阻RF的串联，rL是滤波电感的等效串联电阻，rC是滤波电容的等效串联电阻。对电路作如下假设:所有无源元件为线性不变器件，输入电压源的输出电阻为零，开关器件的输出电容可以忽略不计。

图1  Buck 变换器主电路

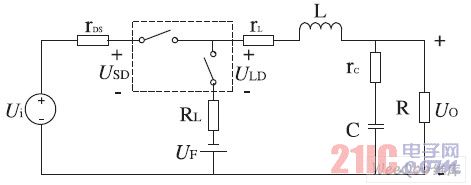
图2  Buck 变换器等效电路

　　能量守恒平均原理是以损耗相等为原则，将电路中各寄生参数产生的损耗之和等效为单一寄生参数产生的损耗，从而简化电路结构。运用能量守恒平均原理，将电路中寄生参数折算到电感直流支路中，通过运用替代定理，将经小信号扰动处理的理想开关由受控电压源和受控电流源替代，进而可获得变换器直流模型和小信号模型。

　　在Buck 变换器中，当开关晶体管导通时，开关管电流与电感电流iL相等；当开关管关断时，开关管电流为零，则一周内开关管电流有效值可计算为：

　　因此，开关管按有效值的开通功率损耗为:

　　按平均值计算的功耗为:

　　根据等效原则:

　　代入式(1)，可以得到开关管S 的通态电阻的等效平均值为:

　　当开关晶体管S 关断，二极管D 导通时，流过二极管的电流iD =iL ≈IL 。当开关晶体管S 导通，二极管D 关断时，流过二极管的电流iD =0，则一周内二极管电流的有效值为:

　　因此，二极管正向电阻按有效值的开通功率损耗为:

　　按平均值计算的功耗为:

　　根据等效的原理:

　　代入式(6 )，可以得到二极管D 的正向电阻的等效平均值为:

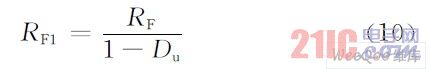
 　　同理可以得到电感L 的等效平均值RL1和电容C的等效平均值RC1为:

图3  考虑寄生参数的Buck 变换器大信号电路模型

　　为了简化模型，利用映射规则将寄生参数折算到电感支路中，可以得到:开关晶体管支路中电路rDS1 =rDS/Du移到电感支路中，等效为DrDS ;二极管支路中电阻移到电感支路中，等效为(1-D)RF ;二极管支路内电压移到电感支路中，等效为(1-D)UF 。并且有如下关系式:

 　　经过整理后的Buck 变换器大信号电路模型如图3 所示。

　　2  直流和小信号模型

　　对Buck 变换器大信号等效电路中的各平均变量分离扰动，分解为相应的直流分量与交流小信号分量之和。令:

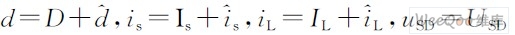
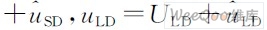
　　将这些公式代入式(12 )和式(13)得:

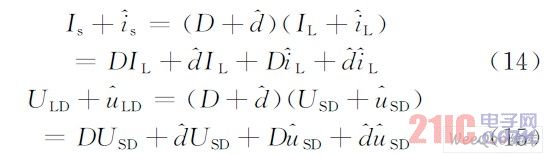
　　忽略其中的高阶微小量，分别得到它的直流和小信号模型如图4 、5 所示。

图4  Buck 变换器的直流模型

 

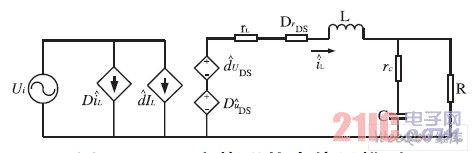
图5  Buck 变换器的小信号模型

　　基于小信号模型，可求出变换器的开环占空比到输出电压传递函数:

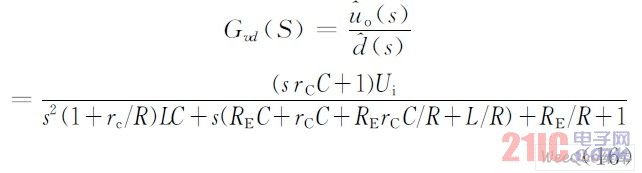
　　式中，RE =DrDS +(1-d)RF +rL 。

　　3  仿真分析

　　为验证所提出模型的准确性，对Buck 变换器进行仿真，参数为Ui =20 。5 V，Uo =10 V，rDS =0。01 Ω，UF =0。45 V，RF =0。03 Ω，L=127 μH，rL =0。11 Ω，C=247 μF，r=5 Ω，开关频率f=50 kHz 。首先利用MATLAB 依据本文模型绘制出变换器传递函数Bode图，再利用仿真软件Saber 通过时域扫频逐个获取变换器在各个频率点处的幅频和相频特性，最后将两种仿真结果进行对比分析。

　　图6 对实际Buck 变换器在连续工作模式下的传递函数Gvd (s )Bode 图的实验结果和能量守恒模型仿真结果进行了比较。由图6 可以看出，Gvd (s )Bode 图实验测试结果和能量守恒模型仿真结果相吻合，表明考虑功率开关管的开通电阻、二极管的正向压降和正向电阻、电感的等效串联电阻以及电容的等效串联电阻的能量守恒平均模型能正确地反映Buck 变换器的特性，揭示了考虑寄生参数建模的必要性。

 

图6  实际Buck 变换器Gvd (s )Bode 图试验结果和仿真模型的比较

　　4  结 语

　　本文基于能量守恒平均原理，通过求取等效平均电阻、电感折算、小信号扰动处理及受控源代换，建立了连续模式下的Buck 变换器模型，给出了传递函数的表达式。仿真表明，能量守恒平均模型能够准确地描述变换器的频率特性。为变换器的稳定性分析提供了理论依据。