文献标识码: A
文章编号: 0258-7998(2010)12-0099-04
Zigbee是近年来兴起的一种无线通信协议,其MAC/PHY由IEEE802.15.4协议[1](以下简称协议)所定义,是一种低数据率的短距离无线通信解决方案,特别适合智能家居[2]、传感器网络等方面的应用。该协议主要面向低成本应用,因此很多文献研究了协议解调算法的简化设计,但是大部分性能牺牲较大。本文从信号最大似然估计的角度出发,导出了两种高效的解调算法,并完成了电路设计。电路仿真表明,在高斯白噪声信道中,该算法在电路规模接近其他非相干解调算法的情况下,性能有5.1 dB的提升。
1 解调方案分析与设计
协议的基带调制方式为:对发送数据进行4 bit符号(Symbol)到32 bit码片(Chip)的直接序列扩频,然后采用半正弦成型的O-QPSK对扩频码片进行调制,流程如图 1所示。

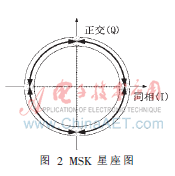
该信号等价于MSK(最小移频键控)信号,其星座图如图 2,发送1时候,信号相位在一个码片周期中沿单位元逆时针旋转90°,发送0则顺时针旋转90°。每个码片是MSK的一个符号,码片速率2 Mchip/s。按照MSK进行解调的扩频码如表 1(由于O-QPSK“偏移”特性,“X”表示该码片需要和下一个符号共同确定)。

协议对于接收机性能的规定是:“在输入信号功率-85 dBm,包长20 B情况下,误包率低于1%”。传统相干解调需要进行频偏的估计和恢复,电路较为复杂;而在常见的信号的非相干解调方案中,过零检测[3]等方案讨论较多,但是算法性能受到频偏影响较为明显。此外,部分文献给出了角度解调的算法,思路是将输入复信号求辐角,对角度进行解调。上述两种算法和无频偏的相干解调相比,有约9 dB(相同误码率所需的信噪比)性能的差距。
对于直接序列扩频信号,传统的解调方法是逐码片解调,然后进行解扩。本文采用不同的思路,直接对扩频的符号进行最大似然估计和解调。带有噪声、频偏的协议信号采样点复数表达式为:


2 算法MATLAB仿真
使用MATLAB对于给出的两种算法进行仿真。首先设置两种参照算法:T1使用频偏估计的MCBR(修正的克拉美罗界,估计方差的一个下界)为方差的正态分布来模拟补偿后残留频偏,然后对补偿后信号相干解调;T2算法使用参考文献[5]频偏补偿后相干解调。
仿真设置:使用MATLAB生成2×106个符号的数据,信道模型采用AWGN模型。
在无频偏情况下,不同算法误码率如图3所示。
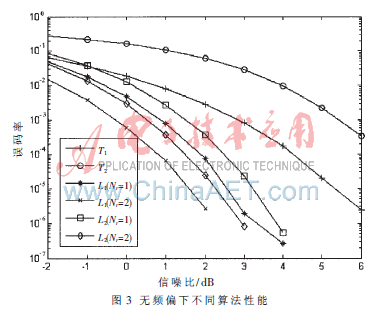
可以看到,L1和L2的算法性能优于“进行频偏补偿相干解调”的算法(主要原因是使用一个符号的数据进行频偏估计性能较差)。而在没有频偏情况下同阶的L1算法性能优于L2算法。
协议规定最大频偏200 kHz,此时误码率如图4。
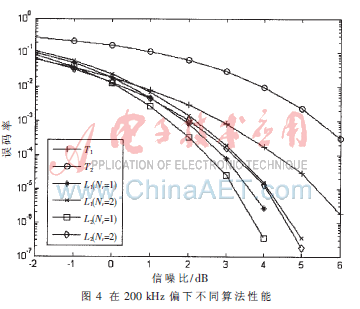
可以看到大频偏下L1算法差于L2。对比两个图可以看到L2算法性能受到频偏影响不大。
在频偏均匀分布的情况下,L1算法性能介于一阶和二阶L2算法之间。均匀分布随机频偏下不同算法性能如图5所示。
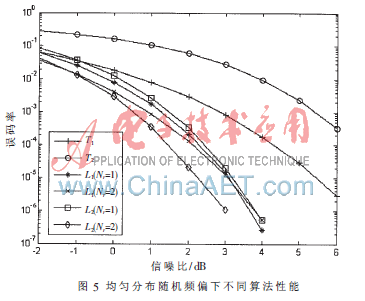
总结仿真结果:L1性能随着频偏的增大而下降;L2算法对于频偏不敏感。因此在小频偏情况下适合选择L1算法,而频偏可能值较大时,应选择L2算法。阶数的增加,增大了解调算法的性能,但同时使L1对频偏敏感度增加;而L2算法阶数提高使得性能有明显提高。电路设计可据此选择算法。
3.1 电路设计
实现解调算法的电路框图如图 6所示。这里以一阶(Nr=d=1)为例,二阶类似。
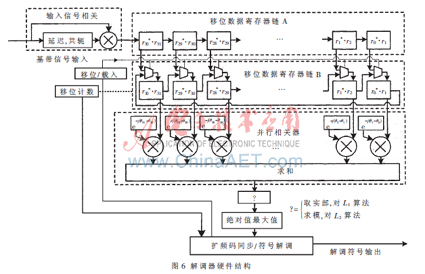

上述相关器的因子为±j,无需使用乘法器,只需将数据进行实部和虚部的交换以及符号变化。相关器输出根据上面讨论的两种算法,进行取实部(对L1)或者取模(对L2)。具体工作原理如下:
扩频信号的解码首先要进行扩频码的同步,查找扩频码的头。协议帧的预同步序列是8个符号0。扩频码具有良好的自相关特性,利用这一点进行同步:A工作在移位状态,B工作在数据载入状态。当一个符号0符号数据载入上述链B中时(如图中的r0* r1到r30* r31为一个符号的样点的自相关),相关器的输出将超过一定的阈值;该点即为同步点。解调器进入同步状态。
进入同步状态以后,获得了扩频码的边界,每当A中移入一个完整的扩频码数据时,B载入一次,移位计数器清零;其他时间B处于循环移位状态。这样在一个新的符号移入A时,B中上一个符号的数据进行循环移位,并计算每一次移位后的相关。根据扩频码的循环特性,记录B在移位过程中相关器输出的绝对值最大时的移位计数器的值,即可得到解调的符号。例如相关输出的绝对值最大在计数0出现,表示解调的符号为0或8;如果移位4位以后出现,表示解调的符号是1或9,以此类推;当相关输出的实部的符号为正则解调符号在0~7内,为负则在8~15内。如果出现最大值位置不是4的整数倍,则根据就近原则确定,以减小同步错误对解调的影响。上述过程介绍中输入信号是一倍采样的,实际接收机中需要对信号进行过采样,则在上述电路中进行修改:假设过采样率Ns,则A和B长度增加为31·Ns,而并行相关器对于寄存器链B将每Ns个数据取一个进行相关运算。其余工作流程类似。
3.2 电路仿真
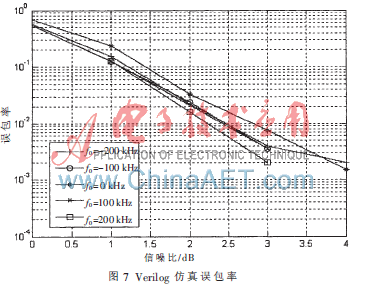
在两种算法以及解调器结构的基础上本文完成了硬件电路的Verilog设计和FPGA验证。以L2为例,使用MATLAB产生测试数据,在0 dB信噪比下,过采样率Ns=4,仿真表明,在低信噪比情况下,相关器仍然具有较明显的输出峰值,可以很好解调。用6 bit的量化数据进行2 000帧(帧的长度为20 B,即40个符号)数据的电路仿真(AWGN信道,使用Synopsys VCS仿真器),模拟完整的帧接收过程,不同频偏下结果如图7,可以看到性能随着频偏变化不大;仿真表明实现1%误包率所需要的信噪比约为2.9 dB。
4 性能总结与比较
简单对比主要的参考文献中给出的协议基带解调算法以及硬件的性能和门数(包括调制和解调),其中“性能”表示实现1%误包率所需要的信噪比,对比如表2。门数中括号中的数据是解调器的门数(0.18 μm工艺)。
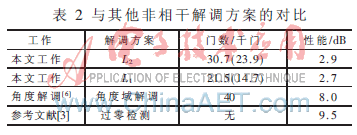
可以看到,本文的工作在硬件规模上与简单的非相干解调算法类似,而在总体的性能上好于传统非相干解调算法约5.1 dB以上(L2算法)。
本文给出了用于Zigbee解调的简单高效的算法,并完成了硬件设计。仿真表明,相比于传统的非相干解调算法,该算法性能提高5.1 dB,同时硬件规模接近。该电路在硬件结构简化的同时保持了较好的性能,降低了模拟前端电路的要求,对于Zigbee接收机设计有着很好的借鉴意义。
参考文献
[1] IEEE Standard for Information Technology-Telecommunications and Information Exchange Between Systems-Local and Metropolitan Area Networks-Specific Requirements Part 15.4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (WPANs)[S]. 2006.
[2] 周游,方滨,王普.基于ZigBee技术的智能家居无线网络系统[J].电子技术应用,2005,31(9):1-3.
[3] YU Yun Feng. A new low-cos demodulator for 2.4 GHz zigbee receivers[J]. 电子学报, 2009(02):252-257.
[4] CHOI Z Y, LEE Y H. On the use of double correlation for frame synchronization in the presence of frequency offset[C]. IEEE International Conference on Communications,1999(2):958-962.
[5] LI En Zheng. Joint frequency offset estimation and timing synchronization for DSSS MSK receiver[C]. Asia-Pacific Conference on Communications,2005:358-361.
[6] 陈培仁.IEEE 802.15.42.4GHz无线个人网实体层之ASIC设计[D].台湾:国立中正大学电机工程研究所硕
士论文,2006.

