随着微机电系统MEMS（Micro Electro Mechanical System）技术的发展，MEMS陀螺以其尺寸小、重量轻、成本低、功耗小等特点，在低成本惯性导航系统中获得了越来越广泛的应用。但受制造工艺及技术水平的限制，目前,MEMS陀螺精度相对传统陀螺要低，其误差成为惯性导航系统误差的主要原因。MEMS陀螺误差一般可分为刻度因子、确定性漂移、随机漂移及随机噪声误差[1]。刻度因子误差和确定性漂移补偿误差可通过标定来实现[2]。因此，随机噪声和随机漂移的处理成为MEMS陀螺数据处理的重点。
    小波阈值去噪[3]是目前最常用的MEMS陀螺去噪方法，其结合了时域分析和频域分析的优点，根据突变信号和噪声信号经过小波分解信号后的不同规律，可很好地实现信噪分离。但若小波分解层数选择不恰当，会造成有用信号被滤除，信号特征被改变的问题。
    陀螺随机漂移建模目前常用的方法是自回归AR(Autoregressive)模型，其具有模型简单、建模灵活的特点[4]。但其属于线性模型，且要求所需建模的序列必须满足平稳性。而陀螺随机漂移往往存在非线性和不平稳性，采用线性建模会引入一定的误差，且AR模型所要求的平稳性一般很难真正满足。函数系数自回归FAR(Functional Coefficient Autoregressive)模型[5]是一种基于非参数、非线性的统计模型，其系数是依赖变量的函数。同AR相比，它在一个更大的模型族中寻找合适的模型，因此能有效减少因模型选择不合适而引入的误差，提高模型的精确性，且其属于非线性模型，更适合用来进行陀螺的非线性漂移建模。
    此外，目前很多参考文献只侧重于对MEMS陀螺进行去噪处理或只对其进行随机漂移建模，未能全面而有效地对MEMS陀螺输出进行数据处理。
    针对目前MEMS陀螺数据处理中存在的问题，本文研究了小波阈值去噪和FAR建模相结合的MEMS陀螺数据处理方法，在小波阈值去噪中采用自适应算法进行小波分解层数的选取;而利用FAR模型对陀螺随机漂移进行建模,并将其应用于实际数据处理中，验证了该数据处理方法的有效性。
1 陀螺输出数据小波阈值去噪
1.1小波阈值去噪的基本原理
　　小波阈值去噪以小波变换为基础，结合了时、频两域分析的优点,根据信号与噪声在各尺度上的小波系数具有不同特性的特点，按照一定的阈值准则处理小波系数。小波阈值去噪包括分解过程、作用阈值和信号重建三个步骤[6]。
1.2 小波阈值去噪分解层数的选取
    小波阈值去噪中的关键问题包括阈值的确定、分解层数的选取以及小波基函数的选取，目前的研究主要集中在阈值的合理选取上,但分解层数在很大程度上也会影响小波去噪的效果。分解层数过多，运算量增大，同时会丢失有用信号；分解层数过少则去噪效果不理想。
    传统分解层数的选取是根据信号的频谱特征来进行的，需首先对信号进行频谱分析。分解层数的选择以去除比运动信号频率高的部分为依据,这在工程应用中是较为不便。因此,很多学者展开了对分解层数的自适应选取方法的研究。这里引用参考文献[7]提出的基于奇异谱分析的分解层数自适应选取算法，其基本原理是利用了小波去噪最优分解层数与小波系数序列的奇异谱斜率之间的对应关系，通过设定奇异谱斜率的阈值来选取最优分解层数。奇异谱分析法的详细介绍可见参考文献[7-8]。
2 陀螺随机漂移建模
2.1陀螺随机漂移的AR建模
    AR模型属于时间序列分析法中的一种线性模型，是利用相邻时间序列之间的依赖性进行分析和建模的。建模前必须对时间序列进行统计处理，保证时间序列满足平稳、正态、零均值的条件。
    自回归AR(p)模型的方程[4,8-10]为：


    模型识别后，需确定AR模型的阶数。此处采用BIC准则来确定最佳阶数。AR(p)模型的BIC准则函数为：

    根据上述方法可获得系数函数在所有区间段上的局部线性近似。
    参数p、d、b、N的选取通过平均均方预测误差APE来确定。APE的计算方法为：对长度为n的序列，给定正整数L和m，要求n>mL，并按图1所示划分序列进行建模和预测，分别计算每段的均方预测误差，再对m个均方预测误差求均值即为平均均方预测误差(APE)[7]。定阶的具体实现过程为：依次使N=1，…,Nmax;p=1,…,pmax;d=1,…,p;b=b0,…,1,分别计算相应的APE，令APE最小的N、p、d、b作为模型的最佳参数。

3 实验结果与分析
    采用上述的数据处理方法对ADIS16355中陀螺输出进行数据处理。以X轴陀螺为例，采集陀螺输出数据，采样间隔为0.02 s，采样时间为20 min，数据总数为60 000。其中前3 200个数据为静态数据，后56 800个数据为动态数据，如图2所示。从图2可看出，陀螺输出中含有大量噪声，主要包括高频成分和低频成分。其中，低频成分表现为相关噪声，即随机漂移，可通过建模为一定的随机过程加以补偿。高频成分表现为白噪声特性,需通过一定的去噪方法加以滤除，以提高陀螺输出的准确性。

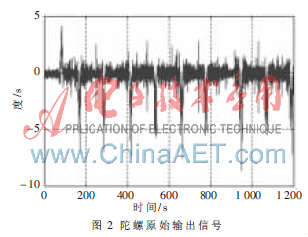
    首先对其进行小波阈值去噪,在MATLAB环境下，选取db5小波，采用基于无偏似然估计的阈值准则(rigsure)和软阈值法，并采用基于奇异谱分析的自适应算法进行最优分解层数的确定，选取的分解层数为8层。小波阈值去噪后的MEMS陀螺输出信号如图3所示，与图2比较可知，小波去噪后，信号中的噪声得到了很大程度的抑制，信噪比大大提高，为随机漂移的建模奠定了基础。

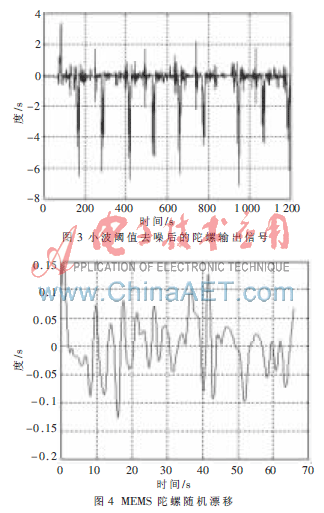
    然后采用陀螺输出的前3 200个静态数据进行随机漂移建模,小波去噪后减去静态数据的均值，认为残差即为陀螺的随机漂移，如图4所示。
    分别建立陀螺随机漂移的AR模型及FAR模型。采用BIC准则及最小二乘参数估计法,得到的模型为AR(5)：

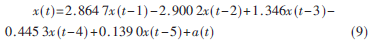
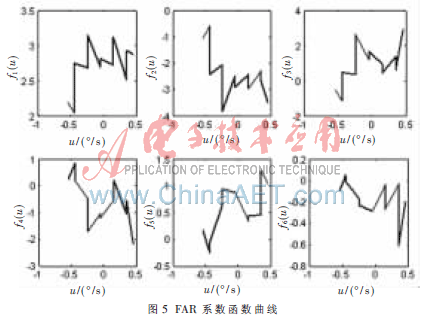
    根据平均均方预测误差(APE)最终确定的陀螺随机漂移的FAR模型的参数为：p=6,d=3,b=0.10,N=5。图5为所估计的FAR的系数函数曲线，横轴为依赖变量u,纵轴为FAR系数函数值。

    针对上述两种陀螺随机漂移建模方法，分别从拟合精度及预测精度两方面进行比较。拟合精度用均方根误差来衡量，结果如表1所示。

    由表1可知：FAR(6,3)拟合误差与AR(5)拟合误差位于同一个数量级，但FAR(6,3)的拟合精度要略高于AR(5)。
    为直观判断两种模型的预测效果，预测精度用均方根相对误差来衡量，其定义为：
  
    两种模型预测均方根相对误差随预测步数增加的变化情况如表2所示。

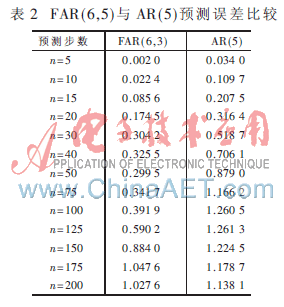
    由表2可知，随着预测步数的增加，两种模型的预测误差均逐渐增大。当预测步数小于125时，FAR(6,3)模型的预测均方根相对误差比AR(5)模型平均减小50 %以上；当预测步数大于150时，FAR(6,3)模型的预测均方根相对误差比AR(5)模型平均减小15%左右。
    通过以上两方面的比较可得：FAR(6,3)模型的拟合精度略高于AR(5),而其预测精度要远远高于AR(5)模型的预测精度，因此，陀螺随机漂移采用FAR(6,3)进行建模更为合适。
    本文针对MEMS陀螺输出中存在大量随机噪声和随机漂移的问题，研究了采用小波阈值去噪滤除随机噪声并利用FAR模型进行随机漂移建模的MEMS陀螺数据处理方法。实验结果表明，该数据处理方法可有效去除陀螺输出噪声，且FAR模型的引入可有效解决MEMS陀螺随机漂移的非线性问题，比AR模型能更精确地反映及预测随机漂移，为随机漂移的实时补偿奠定基础。因此，在组合导航系统中,可采用本文的数据处理方法对MEMS陀螺输出进行处理，提高信噪比，实现陀螺随机漂移补偿，从而提高导航系统的定位精度。
参考文献
[1] PARK M. Error analysis and stochastic modeling of  MEMS-based inertial sensors for land vehicle navigation  applications[D].Canada: CALARY,2004:31-83.
[2] MOHAMMED E D, PAGIATAKI S. Calibration and stochastic modelling of inertial navigation sensor errors[J]. Journal of Global Po-sitioning Systems, 2008,7(2):170-182.
[3] 宋丽君,秦永元,杨鹏翔.小波阈值去噪法在MEMS陀螺仪信号降噪中的应用[J]. 测试技术学报, 2009，23(1):33-36.
[4] NASSAR S. Improving the inertial navigation system (INS) error model for INS and INS-DGPS applications[D].CALGARY,2003:32-82.
[5] 吕永乐. 机载设备工作性能预测建模方法及其应用[D].北京：北京航空航天大学,2009:60-63.
[6] 高志，余海啸. Matlab小波分析与应用[M]. 北京:国防工业出版社,2007:104-114.
[7] CAI Tie, WU Xing. Wavelet-based denoising of speech using adaptive decomposition[C]. Industrial Technology,2008 IEEE International Conference on 21-24 April  2008:1-5.
[8] 蔡铁，朱杰. 小波阈值降噪算法中最优分解层数的自适应选择[J]. 控制与决策,2006，21(2):217-220.
[9] 吴怀宇.时间序列分析与综合[M].武汉：武汉大学出版社，2004:76-94.
[10] NOURELDIN A, EBERTS M D.Perrformance enhancement of MEMS Based INS-GPS integration for low cost navigation Applications[J].IEEE Transactions on Vehicular Technology, V-L.2009,58(3).
[11] 武志辉，惠军.函数系数自回归模型推广形式的Back-Fitting估计[J].合肥工业大学学报，2008，31(6)：985-991.
[12] 惠军，武志辉，缪柏其.改进的函数系数自回归建模方法对上海股市实证分析[J]. 运筹与管理，2007，16(4)：107-110.