近20年来，永磁无刷直流电机因其调速性能好、效率高、寿命长和控制灵活等诸多优点，被广泛地应用于航空航天、汽车、工业和家电等领域。随着科学技术的发展和永磁无刷电机应用领域的不断扩大,特别是数字信号处理器和可编程逻辑器件的广泛应用，推动了伺服电机控制技术向集成化和智能化的方向发展。
　　建立伺服控制系统的仿真模型可以大大提高伺服系统设计效率，及时验证控制算法的合理性，同时可以利用计算机调整系统的结构和控制参数，观察系统在各种结构和工况下的动态和静态特性。多年来，国内外在Matlab中对伺服电机仿真建模进行了广泛研究，并取得了很好的成绩。基于目前伺服电机普遍采用的全数字控制系统，本文根据实际无刷直流电机DSP数字控制系统构建系统模型。利用Matlab/Simulink的强大仿真功能，对传统的伺服控制系统仿真模型作了改进，提出了一种新的仿真模型，经过仿真证明了该方法的有效性。
1 伺服电机的数学模型
    无刷直流电机中的反电动势为梯形波，包含很多高次谐波，并且电感为非线性，因此dq变换理论已经不再适用［1］。本文采用无刷直流电机原有的相变量来建立模型,以两相导通三相六状态星形连接为例，对无刷直流电机的数学模型及电磁转矩等特性进行分析。
    假定：电机定子三相完全对称，空间上相差120°电角度；电感、电阻参数完全相同；转子磁场对称分布；忽略电枢反应；电机气隙磁导均匀，磁路不饱和，不计涡流和磁滞损耗[2-4]。
    由电机学知识可知，定子三相绕组的电压方程可表示为：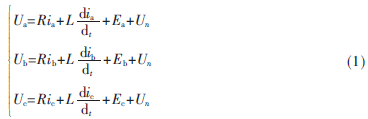

式中，Ua、Ub、Uc和Un分别为三相端电压和中点电压；Ea、Eb、Ec为三相反电动势；ia、ib、ic为三相绕组电流；R、L分别为三相电枢绕组电阻和电感；dt为时间微分。三相方波电流及反电动势波形如图1所示。

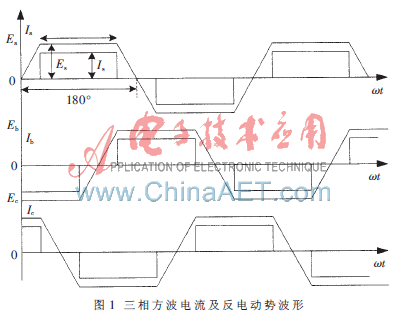
    在电机运行过程中，电磁转矩的表达式为：

2 伺服系统的建模仿真
    国内外在对无刷直流电机仿真建模方面进行了广泛的研究[5-6]，采用了如下建模方法：(1)根据能够反映转子位置变化的绕组电感模块来获得反电动势波形，但这种方法对小电枢电感电机的建模并不可用。因为，如果电机的相电感极小，则转子的位置变化引起的电感变化量就可以忽略不计，从而无法建立模型。(2)采用有限元和FFT法来获得精确的反电动势波形，但结合整个控制系统进行仿真时，仿真速度会大大降低。(3)采用分段线性等方法[7]。但这些方法中电机的换相大都采用电流滞环控制，只适用于理论研究，具体实现时成本较高，开关噪声大。从仿真结果看，上述模型还多属于模拟控制系统，并不适用于目前的全数字控制系统[8,10]。
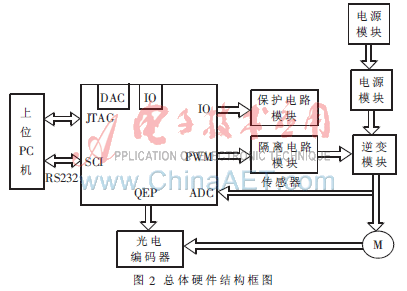
    本文采用无刷直流电机DSP控制系统构建模。实际系统采用TMS320LF2812作为主控制器；IR2130作为三相逆变桥的驱动芯片；MOSFET管组成三相逆变桥,对直流电源输出的母线电流进行采样；DSP输出的PWM信号对电机的相电流和转速进行控制。控制系统采用双闭环控制方案，根据模块化建模思想，可将控制系统分割为各个功能独立的子模块，如图2所示。

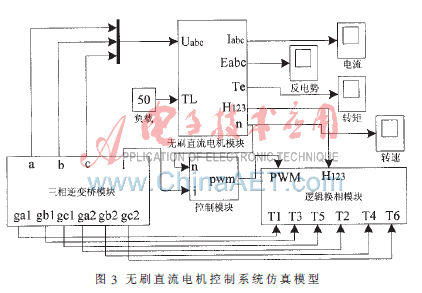
    采用Matlab作为仿真工具，其中的Simulink是用来对动态系统进行建模、仿真和分析的软件包。运用其内部丰富的数学运算逻辑模块和电力电子模块，能建立精确的无刷直流电机及其控制系统模型。图3所示为在Simulink中构建的整个电机控制系统仿真模型，主要包括无刷直流电机模块、三相逆变桥模块、逻辑换相模块和控制模块。

2.1 无刷直流电机仿真建模
    构建无刷直流电机仿真模型是数字控制系统最核心的工作。电机模型采用Simulink子系统封装技术，将电机各个模块集成在子模型中，并通过子系统封装对话框输入电机仿真参数。这样能增强模型整体可读性和灵活性，便于在仿真前修改各种电机参数，从而可以更加直观地比较不同参数下无刷电机控制系统模型的仿真结果。
    另外，结合各类运算模块和电力电子模块，采用S-函数建立无刷直流电机仿真模型。这种建模方法不仅加快了仿真速度，而且由于结合了C语言的优势，从而更容易实现模块的功能。如图4所示，此模块包括电机速度和转子位置2个输入、9个输出信号,分别是三相反电动势信号、霍尔信号和三相电压输入使能信号。电机转子在一个电角度周期内可分为6个状态，在不同状态下，由S-函数输出不同状态值。这种方法克服了在传统电机模型中采用相绕组反电动势时需要削去顶部的正弦波来代替梯形波的缺点，使仿真模型更接近电机控制系统的实际情况。

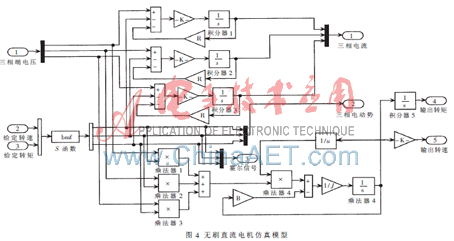
2.2 逻辑换相模块仿真建模
    逻辑换相模块的作用是将无刷直流电机输出的三相位置信号A、B、C，以及由速度控制模块输出的PWM信号，转换为决定逆变器6个开关管120°导通的信号T1~T6和控制速度的脉冲信号，使定子绕组按一定的顺序进行换流。如图4所示，三相逆变桥采用上管调制方式，输出信号T1、T3和T5用来控制三相逆变器上侧功率管的通断，T2、T4和T6用来控制三相逆变器下侧功率管的通断。其逻辑关系式如下：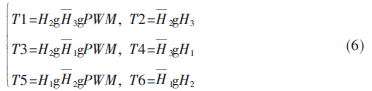

2.3 三相桥式逆变器模块仿真建模
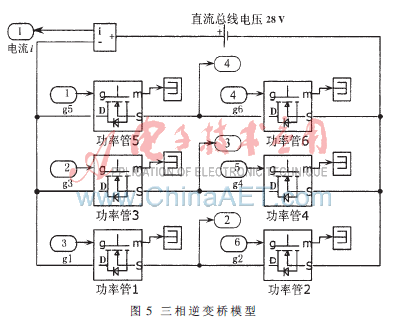
    采用Power Electronics模块库中的MOSFET功率管和直流电源模块，可以构建三相桥式逆变器的模型，输出无刷直流电机所需的三相电压信号。三相逆变桥仿真模型如图5所示,封装后的模型如图2中的逆变模块。仿真前，必需根据实际系统中的功率管的工作特性，对逆变桥中的开关管导通压降、续流二极管导通电阻和寄生电容等参数进行设置,以便能够得到正确的仿真结果。

2.4 控制模块仿真建模
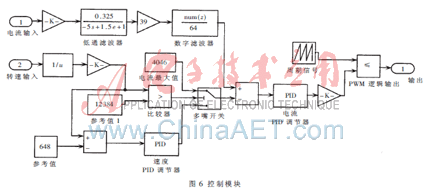
    根据无刷直流电机全数字控制方法构建出的数学模型如图6所示。由于转速和电流调节器都是以参考值与反馈值的偏差作为输入,经PID调节器调整后生成PWM占空比，故可直接调用Simulink中的Discrete PID Controller模块作为转速和电流数字PID调节器。为使仿真模型更具有实用性，仿真前应先将各种参数转变为DSP中相应的内存值或寄存器值，然后通过子系统封装对话框设置PID参数、调节器周期和最大饱和输出等。

3 仿真分析
    仿真时PID参数的选取对控制系统很重要，应综合PID 3个参数变化所带来的影响，具体操作可以按先比例后积分再微分的顺序调试参数。无刷直流电机参数为：定子相绕组电阻0.5  ?赘；转动惯量0.089 kg·m2；极对数4；直流电源200 V;电感1.76 mH；额定转速1 500 rad/min。无刷直流电机采用两相导通三相六状态星形连接方式，每隔60°电角度换相1次，每个功率管通电120°，每个绕组通电240°，其中正向和反向各通电120°。
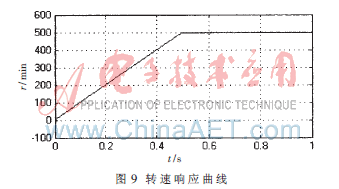
    为了验证控制系统的静态和动态特性，电机空载起动，给定转速为500 rad/min，在系统运行0.5 s时加入负载。得到的系统转矩、转速、三相反电动势和相电流仿真曲线如图7~图9所示。

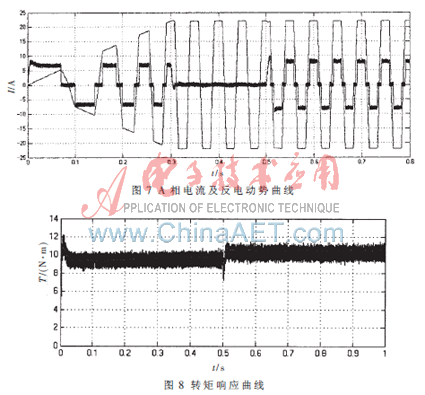
    由仿真波形可看出，在参考转速下，系统响应快且平稳，图7中相电流和三相反电动势波形与图1中的理论波形完全相符,并且根据图中电机起动阶段的反电动势波形，可以得出电机的每次换相时间，使得无刷直流电机的仿真模型具有很好的指导作用，方便了实际系统的分析和设计。
    仿真结果表明,起动阶段由于系统保持转矩恒定，不会产生大的转矩脉动和相电流冲击。在图9中可以看到，当t=0.5 s突加负载时，转速会产生波动，这主要是由电流换向引起的，但能够迅速恢复到平稳运行，稳态运行时无静差。仿真试验表明了本文所提出的这种新型直流电机模型的有效性及控制系统的合理性。

    本文在分析直流无刷电机系统的基础上，提出了一种新型的基于Matlab/Simulink的直流无刷控制系统建模仿真方法，该模型采用经典的转速和电流双闭环控制方法进行了测试。仿真结果表明，其模型的输出波形与理论分析相吻合，系统运行平稳，具有良好的静、动态特性。采用该仿真模型可以灵活地实现各种控制算法和控制策略，能有效地节省系统设计周期，加快实际系统设计和调试进程，为分析和设计直流无刷电机控制系统提供了一个理想的实验平台，也为实际电机控制系统的设计提供了新的思路。  
参考文献
[1] 吴恒, 王淦泉, 陈桂林. 基于SIMULINK的PMSM控制器的建模与控制仿真[J]. 红外, 2010,32(2):29-34.
[2] 赵跃齐, 马瑞卿, 席鹏. 一种新型直流无刷电动机数字控制器建模与仿真[J]. 微电机, 2009,42(3):60-63.
[3] 林飞, 杜欣. 电力电子应用技术的MATLAB仿真[M].北京:中国电力出版社, 2009:255-260.
[4] 王澍, 林辉. 基于TMS320F2812的无刷直流电机伺服系统设计[J]. 微电机, 2008,41(6):44-47.
[5] 解后循, 高翔. 基于S-函数的直流电动机自适应控制系统建模[J]. 微电机, 2009,42(3):68-72.
[6] JIAO G D, RAHN C D. Field weakening for radial force reduction in brushless permanent-magnet DC motors[J]. IEEE Transactions on Magnetics. 2004,40(5):3286-3292.
[7] 王淑红, 张朝山, 武瑞兵. 分段式永磁同步电机控制系统及动态仿真[J]. 微特电机.2009(5):39-43.
[8] 孙自勇, 李广波, 侯强. 基于DSP的无刷直流电机调速系统的研究[J]. 电力系统保护与控制, 2009,37(10):106-110.
[9] 黄科元, 黄守道. 基于Matlab电机系统模块的电机调速系统仿真[J]. 微电机, 2009,42(1):63-66.
[10] 毕海悦, 张东来, 孙宝奎. 一种无刷直流电动机的简捷建模及控制方法[J]. 微电机,2009,42(8):50-52.