1推理控制" title="推理控制">推理控制的CVCF电源的硬件构成
推理控制的CVCF电源系统构成如图1所示,控制电路见图2。
系统采用8031作为CPU,外扩8K的EPROM2764,用于存放监控程序、推理控制、键控及显示程序。扩展一片DAC0832,以便输出阶梯正弦波,其片选信号CS接74LS138的Y0口,选通地址为#1FFFH。DAC0832按单缓冲工作方式,使输入寄存器处于锁存状态,ILE接+5V,WR1接CPU的写信号WR,DAC寄存器处于不锁存状态,所以将WR2和XFER直接接地,DAC0832接成单极性输出,参考电压为+5V,输出0~5V的电压。![]() 扩展一片ADC0809,实现对整流后的直流电压进行采样的功能,8031的WR和74LS138的Y1口经一个或非门接ADC0809的STAR和ALE端,来控制ADC0809的启动和地址锁存。8031的RD和74LS138的1口经或非门接ADC0809的OE端,控制信号的输出。ADC0809的CLK由8031的ALE上信号经过2分频以后提供,EOC经反向器作8031的INT1中断请求输入线,要求CPU从P0上读取A/D转换后的数字量。ADC0809的IN0和采样保持器LF198的输出端相连,故IN0上输入的0~15V范围的模拟电压经A/D转换后,可由8031通过程序从P0口输入到内部RAM单元。
扩展一片ADC0809,实现对整流后的直流电压进行采样的功能,8031的WR和74LS138的Y1口经一个或非门接ADC0809的STAR和ALE端,来控制ADC0809的启动和地址锁存。8031的RD和74LS138的1口经或非门接ADC0809的OE端,控制信号的输出。ADC0809的CLK由8031的ALE上信号经过2分频以后提供,EOC经反向器作8031的INT1中断请求输入线,要求CPU从P0上读取A/D转换后的数字量。ADC0809的IN0和采样保持器LF198的输出端相连,故IN0上输入的0~15V范围的模拟电压经A/D转换后,可由8031通过程序从P0口输入到内部RAM单元。
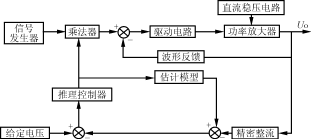
图1推理控制的CVCF系统原理图
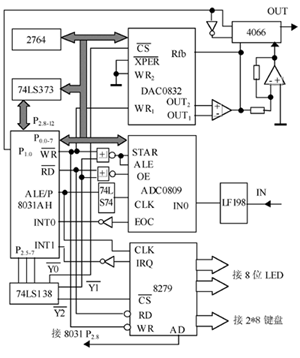
图2推理控制的CVCF电源控制电路图
扩展一片8279,作为扩展的I/O口,接8个LED,以完成显示目标频率、目标电压和反馈电压的功能。8个LED接成共阳极。8279和8031的连接无特殊要求,除数据线P0口、WR、RD可直接连接外,CS由74LS138的Y2口进行片选。时钟由ALE提供,A0接8031的P2.0口,中断请求IRQ经反向器与8031的INT0相连。
8279同时扩展键盘的接口,实现运行、停止、清零、复位功能键的控制。规定扫描线(SL0-SL1)为列线,在此以连接74LS138的输出T0和T1为列线,实现2*8的键盘功能。回复线(RL0-RL7)为行线。
由8031的P2.5、P2.6、P2.7口经74LS138进行地址译码,各扩展芯片的地址由此确定。
2系统软件设计
应用软件分为四大部分:振荡部分、采样部分、调幅部分、通信部分。为了防止严重干扰时“飞”程序,在每个程序之间安放软陷阱,即在各个子程序之间放入几条NOP指令。这样,发现异常时,可强制从头执行。
在软件设计中采用模块化子程序结构,其主程序和推理控制子程序的流程结构见图3。
(1)振荡器子程序
该程序模块要求得到一个频率可调的高频率稳定度的阶梯正弦波。要求频率可调范围为45Hz~65Hz,精度要求为0.1Hz。
在振荡程序中,采用8031的T1定时方法,因为T1工作方式不占用CPU时间。在整个单片机运行期间,振荡部分的定时是自始至终的,故采用T1定时方式2(可以自动重新装入的8位定时器/计数器)进行定时,在不占用CPU的时间里,CPU可以处理其它程序和任务。
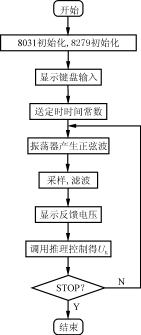
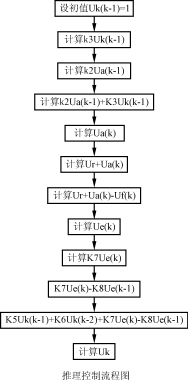
图3程序流程图
将一个正弦波周期分为正半周和负半周两部分,半波时间为1/(2f),将这半波时间分成90份,则定时时间为t=1/(180f),代入T=28-t·fo/12的T1初值计算公式(式中fo为晶振频率),得出定时时间常数,可将45Hz~65Hz的定时时间都算出来并列成表格(如表1所示),设置一个查表程序,在输出不同频率时从表上调取不同的T值。
表1定时时间常数表
| 频率 | 时间常数 | 频率 | 时间常数 |
|---|---|---|---|
| 45Hz | T=C2H | 56Hz | T=CEH |
| 46Hz | T=C3H | 57Hz | T=CFH |
| 47Hz | T=C5H | 58Hz | T=D0H |
| 48Hz | T=C6H | 59Hz | T=D0H |
| 49Hz | T=C7H | 60Hz | T=D1H |
| 50Hz | T=C8H | 61Hz | T=D2H |
| 51Hz | T=C9H | 62Hz | T=D3H |
| 52Hz | T=CAH | 63Hz | T=D3H |
| 53Hz | T=CBH | 64Hz | T=D4H |
| 54Hz | T=CCH | 65Hz | T=D5H |
| 55Hz | T=CDH |
表2正弦波数据表
| θ | U | DEC | HEX | θ | U | DEC | HEX |
|---|---|---|---|---|---|---|---|
| 0 | 0.078 | 0 | 00H | 46 | 1.797 | 92 | 5CH |
| 2 | 0.078 | 4 | 04H | 48 | 1.856 | 95 | 5FH |
| 4 | 0.176 | 9 | 09H | 50 | 1.914 | 98 | 62H |
| 6 | 0.254 | 13 | 0DH | 52 | 1.973 | 101 | 65H |
| 8 | 0.352 | 18 | 12H | 54 | 2.031 | 104 | 68H |
| 10 | 0.430 | 22 | 16H | 56 | 2.070 | 106 | 6AH |
| 12 | 0.527 | 27 | 1BH | 58 | 2.129 | 109 | 6DH |
| 14 | 0.606 | 31 | 1FH | 60 | 2.168 | 111 | 6FH |
| 16 | 0.684 | 35 | 23H | 62 | 2.207 | 113 | 71H |
| 18 | 0.781 | 40 | 28H | 64 | 2.246 | 115 | 73H |
| 20 | 0.860 | 44 | 2CH | 66 | 2.285 | 117 | 75H |
| 22 | 0.938 | 48 | 30H | 68 | 2.324 | 119 | 77H |
| 24 | 1.016 | 52 | 34H | 70 | 2.324 | 120 | 78H |
| 26 | 1.094 | 56 | 38H | 72 | 2.380 | 122 | 7AH |
| 28 | 1.171 | 60 | 3CH | 74 | 2.402 | 123 | 7BH |
| 30 | 1.250 | 64 | 40H | 76 | 2.422 | 124 | 7CH |
| 32 | 1.328 | 68 | 44H | 78 | 2.441 | 125 | 7DH |
| 34 | 1.406 | 72 | 48H | 80 | 2.461 | 126 | 7EH |
| 36 | 1.465 | 75 | 4BH | 82 | 2.481 | 127 | 7EH |
| 38 | 1.543 | 79 | 4FH | 84 | 2.481 | 127 | 7EH |
| 40 | 1.602 | 82 | 52H | 86 | 2.5 | 128 | 80H |
| 42 | 1.680 | 86 | 56H | 88 | 2.5 | 128 | 80H |
| 44 | 1.738 | 89 | 59H | 90 | 2.5 | 128 | 80H |
T1定时时间到,则调用振荡器子程序,由DAC0832输出正弦波,正弦波的产生也是通过查表得到,将半波分成90份,即每2度为一个阶梯,用MATLAB编一小程序将所需数列成表格,每隔时间t查表一次,当查表90次后,通过DAC0832的输出可得出一个半波,再通过反向器叠加后得一正弦波。各阶梯值对应的角度、输出电压及输入数字量如表2所示。

图4阶梯正弦波形图
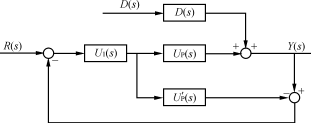
图5推理控制的CVCF系统结构图
此表所得阶梯正弦波如图4所示。这样可得到频率稳定度高的阶梯正弦波。
(2)推理控制子程序及算法
离散化推理控制的基本思想是,当系统的采样频率足够高时,采样系统的特性接近于连续变化的模拟系统,因而可以忽略采样开关和保持器,将整个系统看成是连续变化的模拟系统,从而用s域的方法校正装置D(s)。再使用s域到z域的离散化方法求得离散传递函数D(z)。设计的实质是将一个模拟调节器离散化,用数字控制器取代模拟调节器。设计的基本步骤是,根据已有的连续模型,按连续系统理论设计模拟调节器,然后按照一定的对应关系将模拟调节器离散化,得到等价的数字控制器,从而确定计算机的算法。![]() 首先将离散化令K1=250,
首先将离散化令K1=250,
T1=0.015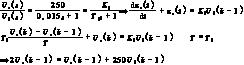
![]() 再将离散化
再将离散化
得308Uk(k)=490Uk(k-1)-185Uk(k-2)
+19Ue(k)-5Ue(k-1)
又Uk(k)=Ur-[Uf(k)-Uc(k)]
∴2Ua(k)=Ua(k-1)+250Uk(k-1)(1)
Ue(k)=Ur-[Uf(k)-Ua(k)](2)
308Uk(k)=490Uk(k-1)-185Uk(k-2)
+19Ue(k)-15Ue(k-1)(3)
当根据(1)、(2)、(3)可得推理控制的输出
令K1=2,K2=1,K3=250,K4=308,K5=490,K6=185,K7=19,K8=15
∴K1Ua(k)=K2Ua(k-1)+250Uk(k-1)(1)
Ue(k)=Ur-[Uf(k)-Ua(k)](2)
K4Uk(k)=K5Uk(k-1)-K6Uk(k-2)
+K7Ue(k)-K8Ue(k-1)(3)
3推理控制的CVCF抗扰性能分析
推理控制的CVCF是一个输出可测、而扰动不可测的系统,设电源的输出为Y(s),输入为R(s),扰动为D(s),此时的电源不需要二次输出和估计器,只需一个估计模型,推理控制的CVCF系统结构如图5所示。
此时的系统输出为![]() 推理控制器Gi(s)=Gf(s)/Gp(s),当Gp(s)=Gp(s)时,系统输出为
推理控制器Gi(s)=Gf(s)/Gp(s),当Gp(s)=Gp(s)时,系统输出为
Y(s)=Gf(s)R(s)+[1-Gf(s)]B(s)D(s)
当Gp(s)≠Gp(s)时,系统的输出为![]() 当滤波器的稳态增益为1时,在给定的阶跃扰动下,系统的主要输出Y(s)=R(s);在阶跃扰动不可测的情况下,系统的主要输出稳态偏差为Y(0)=0。
当滤波器的稳态增益为1时,在给定的阶跃扰动下,系统的主要输出Y(s)=R(s);在阶跃扰动不可测的情况下,系统的主要输出稳态偏差为Y(0)=0。
可见,系统具有非常好的性能,不管模型有何种误差,系统的主要输出总是稳态无偏差的,而且控制系统的可调参数很少。

