0 引 言
随着数字信号处理技术的日臻完善以及数字处理器价格的不断降低,数字控制在DC/DC" title="DC/DC">DC/DC 变换器中得到广泛应用。与模拟控制相比,数字控制具有更加优越的控制性能、更加稳定的系统输出,以及易于实现电源系统的智能化管理等诸多优势。
数字PID 控制因其算法简单、鲁棒性好及可靠性高,广泛应用于DC/DC 变换器的数字控制领域。Buck" title="Buck">Buck 型变换器包括Buck 变换器及其衍生的全桥变换器。当前,数字PID 参数往往通过试凑法整定,耗时费力,同时控制性能欠佳、适应性较差。长期以来,人们一直在寻求更加有效的数字PID 参数整定方法。
1 数字控制Buck 型变换器系统结构
数字控制Buck 型变换器的系统框图如图1 所示。反馈控制回路中包含AD 采样器、误差生成器、PID 控制器以及PWM 波形产生器等模块,所有模块均以数字处理芯片作为载体,通过编程方式实现。
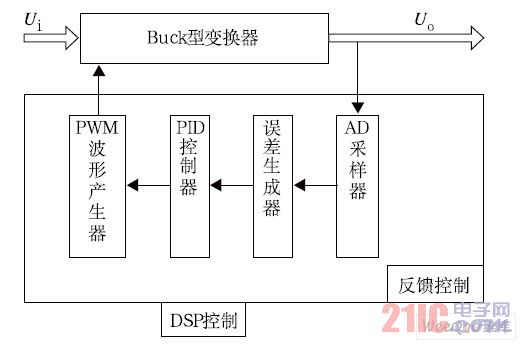
图1 数字控制Buck 型变换器系统框图
2 数字PID 控制器设计
数字系统是离散系统,但如果采样周期足够小,则数字系统可近似于连续系统。采用频域补偿设计方法实现模拟PID 控制器的参数整定,通过连续系统离散化处理,可最终实现数字PID 控制器的参数设计。
2 .1 模拟PID 控制器的参数整定
连续导电模式(CCM)下,Buck 型变换器控制对象的传递函数为:
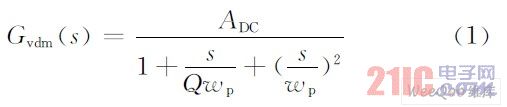
直流增益:
ADC =nUi/Um,UM为PWM 产生器的锯齿波峰峰值;极点角频率: ;;品质因数:Q=R√C/R。
;;品质因数:Q=R√C/R。
Buck 型变换器的典型频率特性曲线如图2 所示。
由频率特性曲线可知:
(1)幅频特性的低频段曲线平坦,欲消除闭环系统的稳态误差,补偿网络的设计应至少含有一个积分环节;(2)主极点wp由LC 输出滤波器产生,表现为一个双重极点,产生180°的滞后相移,系统相位裕量偏低。

图2 连续导电模式(CCM)下Buck 型变换器频率特性曲线
模拟PID 控制器的传递函数为:
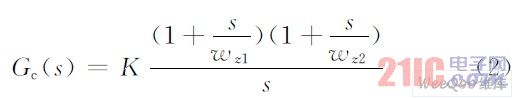
其比例、积分、微分形式为:

式中:Kp =K(wz1 +wz2 )/(wz1 wz2 );Ki =K;Kd =K/(wz1 wz2 )。
模拟PID 控制器的典型频率特性曲线如图3 所示。补偿网络可提供一个原点处极点用以消除系统的静态误差,同时提供两个零点可补偿主极点造成的180°滞后相移,有效提高系统的相位裕量。
在分析了Buck 型变换器及模拟PID 控制器典型频率特性的基础上,采用频域补偿设计法配置补偿网络零极点,实现模拟PID 控制器的参数整定。
模拟PID 控制器零极点配置原则如下:
(1)选择补偿后系统开环传递函数的穿越角频率:
穿越角频率wc一般取1/10 ~1/5 的开关角频率ws处,以在保证系统稳定性的前提下,使输出响应具有良好的动态特性;(2)确定补偿网络两零点角频率:补偿网络的两零点角频率wz1 、wz2设计为控制对象主极点角频率wp的1/2 左右,以补偿主极点产生的180°滞后相移,提高系统的相位裕量;(3)计算补偿网络的增益值:在穿越角频率wc处补偿后系统开环传递的增益为零,即|Gvdm(s )|s =jwc =1/|Gc (s )|s =jwc ,据此计算补偿网络增益值K。
按照以上步骤即可完成模拟PID 控制器参数(Kp 、Ki 、Kd )的整定。
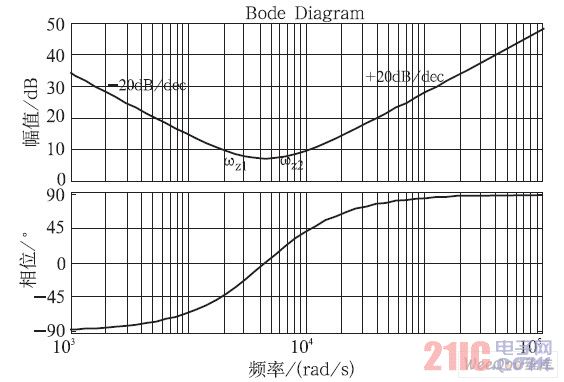
图3 模拟PID 控制器典型频率特性曲线
2 .2 数字PID 控制器的参数设计
数字PID 控制器的控制算式为:
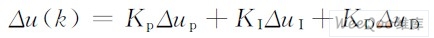
式中:Δup =e(k)-e(k-1 );Δu1 =e(k);ΔuD =e(k)-2e(k-1)+e(k-2)。
模拟PID 控制器参数整定完成后,将模拟控制器离散化即可实现数字PID 控制器的设计。本文选用后向差分法作为连续系统离散化方法。
后向差分公式为:
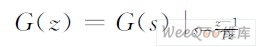
选取采样周期T,对式(3 )进行离散化处理,整理得:
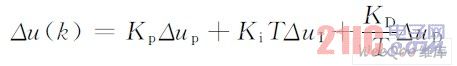
将上式与数字PID 控制算式对比,可得模拟PID控制器" title="PID控制器">PID控制器参数离散化公式:
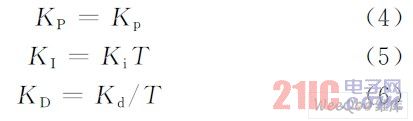
3 Buck 型变换器数字PID 控制器设计实例
仿真用Buck 及全桥变换器的电路参数如表1 所示,数字PWM 脉冲产生器均按D=u(k)/M 设计,其中M=4(M 对应于模拟PWM 产生器的锯齿波峰峰值Um)。
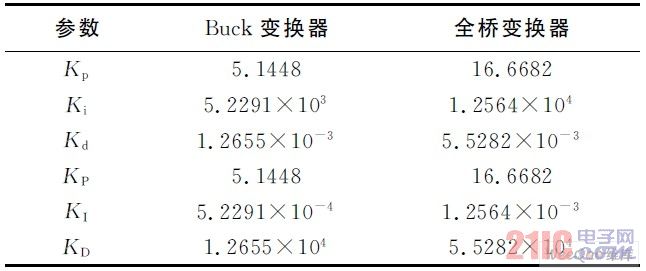
模拟PID 控制器零极点均按照以下方式配置:wc=1/5ws ,wz1 =wz2 =1/2wp ,则模拟及数字PID 控制器整定参数如表2 所示,采样周期T=1×10-7s 。
表1 仿真用Buck 及全桥变换器电路参数

表2 仿真用Buck 及全桥变换器模拟及数字PID 控制器整定参数
根据图1 所示的数字控制Buck 变换器系统框图,依据电路参数及数字PID 控制器整定参数,在MATLAB/SIMULINK 仿真环境中建立数字控制Buck 及全桥变换器仿真模型,仿真结果如下:
额定负载条件下,数字控制Buck 及全桥变换器输出电压响应如图4 所示。

图4 额定负载条件下输出电压响应
额定负载突变至50 %额定负载条件下,数字控制Buck 及全桥变换器的输出电压响应如图5 所示。

图5 负载突变情况下,输出电压响应
4 结 论
仿真结果表明,采用频域补偿设计方法整定模拟PID 控制器参数进而通过连续系统离散化方法设计实现的数字PID 控制器,能够满足Buck 型变换器系统的控制要求,输出响应具有良好的静态与动态特性。

