摘   要: 提出一种可重构" title="可重构">可重构AES硬件架构,对加/解密运算模块和密钥扩展模块进行了可重构设计,使其能够适配" title="适配">适配128bit、192bit、256bit三种" title="三种">三种密钥长度的AES算法,并针对列混合模块进行了结构优化" title="结构优化">结构优化。在FPGA上进行了验证与测试,并在0.18μm SMIC工艺下进行了逻辑综合" title="逻辑综合">逻辑综合及布局布线。结果表明其核心时钟频率为270MHz, 吞吐量达到3.4Gb/s,能够满足高性能的密码处理要求。 

    关键词: 可重构; AES; 密钥扩展;列混合

    随着信息化和网络化的飞速发展,计算机之间传输数据的安全性已愈发重要。对数据进行加密是保护秘密信息的一种重要手段,然而,随着计算机运算速度、密码分析技术和芯片处理能力的不断发展,一些传统的加密算法的安全强度已经很难适应新的安全需要。因此,AES应运而生。2000年10月,美国国家标准技术研究所(NIST)通过公开征集和讨论最终宣布将Rijndael算法作为新的高级加密标准^[1]。Rijndael具有抗攻击能力强、密钥建立时间短、灵敏性好和内存需求小的特点。 

    本文在设计AES算法IP核时,综合考虑速度和面积等因素对硬件实现的影响,一方面对列混合模块进行了结构优化,另一方面对密钥扩展模块进行了可重构^[2]设计,使其能够适配密钥长度为128bit、192bit和256bit的三种AES算法,从而既提高了处理速度,又有效节省了硬件资源。本设计在经过FPGA验证后,采用Synopsys逻辑综合工具Design Compiler进行逻辑综合和优化。结果表明,该设计能够满足高性能密码处理要求,可以作为CPU核的外围模块。 

1 AES算法介绍 

    AES算法是一个迭代型分组密码。其明文分组长度为128bit,密钥分组长度可以分别指定为128bit、192bit、256bit,即AES-128、AES-192和AES-256。它们的加/解密圈数分别为10、12和14。AES加/解密算法的输入是一个128bit的数据块,此数据块被编排为一个被称作状态矩阵的4×4矩阵,AES的所有变换都是基于该状态矩阵的。类似地,种子密钥也用一个以字节为元素的矩阵阵列表示,该阵列有4行,列数记为N_k,对应三种密钥长度,N_k分别为4、6、8。AES算法流程如图1所示。 

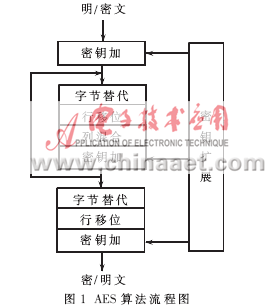
    算法的操作步骤为:初始的密钥加、(N_r-1)轮迭代以及一个结尾轮。其中,轮迭代又分为四步,即字节替代(ByteSub)、行移位(ShiftRow)、列混合(MixColumn)、密钥加(AddRoundKey)。在结尾轮运算中不进行列混合变换。 

    AES解密算法有两种实现方案^[3],其一是直接使用加密算法的逆算法,在这种实现方案中,解密算法所使用的基本运算都是加密算法的逆运算,但所使用的子密钥与加密算法相同,只是使用顺序与加密算法相反。其二是采用等效解密算法,其架构与加密算法非常类似,但所使用的子密钥与加密算法不同。本文在硬件实现时,为减少资源占用,将加密和解密模块整合到一个模块中实现,故采用等效的解密流程。 

2 可重构AES算法的设计与实现 

2.1 整体架构 

    AES算法结构简单,只需要逻辑运算和查找表运算,易于实现,灵活性强。它不需要大量复杂的乘法运算,加解密速度快,且轮函数具有良好的统计特性,并行执行度高,十分有利于硬件设计与实现。本设计从节约资源角度出发,将加密和解密算法整合到一个模块中实现。图2所示是可重构AES算法的整体电路架构。电路由输入输出模块、可重构运算模块、可重构密钥扩展模块和控制模块四部分组成。 

    Start为启动信号。当LoadData信号或LoadKey信号有效时,外部明/密文或种子密钥通过In/Out端口分别注入到可重构加/解密运算模块或可重构密钥扩展模块中进行相应变换。KeySize信号用来选择该模块被重构成哪种密钥长度的AES算法。当其为“00”时,该模块重构成AES-128;当为“01”时重构成AES-192;为“10”时重构成AES-256。Enc_Dec为加/解密信号,用来指示加密或解密操作。当Busy信号有效时,表示内部正在进行加/解密处理或密钥扩展运算。 

    在可重构加/解密运算模块中,ByteSub所使用的S-box和InvS-box主要有三种实现方法,即查找表法、多项式法以及ROM替代法。本文采用存储器资源来进行实现,不占用其他硬件资源,而且可以减少延时。AddRoundKey采用简单的异或逻辑实现。 

2.2 关键模块的设计实现 

2.2.1 密钥扩展模块 

    密钥扩展是以4字节字为元素的一维阵列,表示为W[N_b×(N_r+1)],其中前一个字取为种子密钥,以后每个字按递归方式定义。本文针对密钥扩展模块进行了可重构设计,其单元结构如图3所示。 

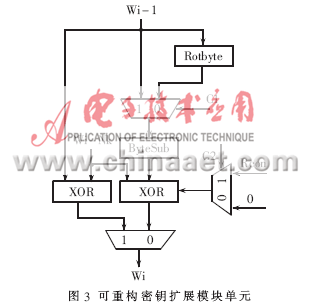
    在图3中,对C1、C2、C3进行相应配置就能使该单元分别适配三种密钥长度的密钥扩展算法。具体的配置参数如表1所示。

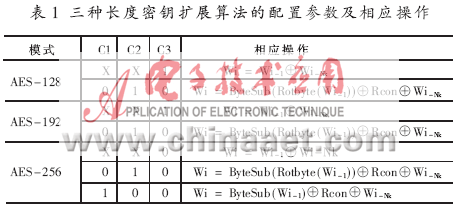
    在加/解密过程中每一轮需要128位的轮子密钥,子密钥的生成可以与密码处理并行进行,采用这种方式扩展密钥可以节省存储空间,但会增加芯片的动态功耗,并且由于解密运算所使用的子密钥是由加密子密钥经过列混合运算得到,故解密时的密钥扩展比加密时的密钥扩展要多用一倍的时钟,这将使运算模块长期处于等待状态,制约解密过程的实现,导致处理性能降低。通常,在实际应用中种子密钥不会频繁改变,所以本文采用外部扩展方式,即通过预计算将扩展出的子密钥保存在RAM中,进行密码处理时再从RAM中读出各轮子密钥参与运算。这种方式灵活性强,对提高整体性能有很大帮助。 

2.2.2 行移位模块 

    行移位只是完成信号在不同输入输出之间的切换,不占用任何触发器、门阵列资源,只占用布线资源。本文采用硬连线方式实现该模块,延时小且实现简单。通过配置,该模块能够分别实现三种密钥长度所对应的行移位。该模块结构如图4所示。 

2.2.3 列混合模块 

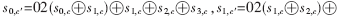
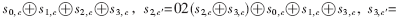
    列混合变换被定义为系数在有限域GF(2⁸)上的四次多项式矩阵乘法^[1],加密过程是在GF(2⁸)上乘01、02、03,解密过程相对复杂,是在GF(2⁸)上乘09、0E、0B、0D。为了简化实现,将矩阵乘法展开并整理。以加密过程为例可得: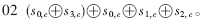对解密过程也进行相应整理,经比较可以得知加密和解密两种操作函数中存在可共享的部分,于是将两种操作函数整合在一起,从而简化了列混合模块的实现过程,节约了硬件资源。 

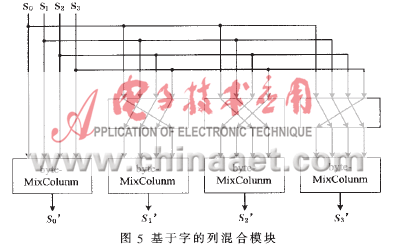
    图5给出了以字为单位的硬件电路模型。在以字节为单位的列混合模块中,x乘法电路是最重要的单元。对于任意给定的输入数据b(7:0),当执行x乘运算时,首先将b(7:0)左移1位得到数据b(6:0)&‘0’;其次判断数据最高位b(7)的值。若b(7)=0,则输出数据为b(6:0),否则,输出数据为b(6:4)&(“11011”xor (b(3:0) &‘0’))。因此,x乘法可以用字节内左移一位和紧接着的一个与0x1b的条件位异或来实现。本文对其进行了优化设计,如图6所示。 

3 性能评价 

3.1 密码处理性能 

    整个设计是在Quartus Ⅱ开发平台上采用Verilog语言实现的,并将设计文件在Quartus软件下进行编译、仿真和FPGA下载验证。表2给出了采用FPGA实现时的性能和资源占用情况。

    本设计在经过FPGA验证后,采用0.18μm CMOS标准单元库编写约束文件,使用Synopsys Design Compiler工具进行逻辑综合、优化,在ModelSim工具上仿真,其综合结果如表3所示。

3.2 与其他实现方案的比较 

    在不考虑初始配置时间和数据输入/输出时间并假定数据、子密钥已经准备完毕的情况下,在参考文献[4]中提出的方案其速率为1.83Gb/s,参考文献[5]中提出的方案速率为0.61Gb/s。AES算法基于SP网络结构设计,数据处理并行度高,本文是按照其基本结构实现该算法时选取的数据。如前所述,本设计能够较好地适配AES算法,加/解密速率达3.4Gb/s。由此可见,本方案在速度上具有明显的优势,同时对系统资源的消耗很少,具有很好的性价比。 

    本文对AES算法的运算模块和密钥扩展模块进行了可重构设计,对轮结构中的列混合模块进行了结构优化,并给出了AES算法在ECB模式下的设计方案。在该方案基础上做进一步改进便能实现AES算法的CBC、OFB、CFB模式。此外,本文在分析AES算法基础上,分别用FPGA和ASIC对本文提出的方案进行了高速硬件实现。该方案同样适用于Altera公司的其他FPGA芯片及Xinlinx公司的FPGA器件等,具有很好的通用性。 

参考文献 

[1] DANMEN J, RIIJMEN V. AES Proposal : Rijndael.AES algorithm submission, AES home page: http://www.nist.gov/aes, 1999-09. 

[2] SIGH H, LEE M H, LU G, et a1.An integerated reconfigurable system for data-parallel and computation-intensive applications[J]. IEEE Transcations on Computer, 2000,49 (5):465-481. 

[3] 朱信贤.全功能AES密码引擎之超大型积体电路架构设计[D].台湾:台湾国立云林科技大学,2002. 

[4] KUO H, VERBAUWHEDE I, SCHAUMONT P. A 2.29 Gbits/sec, 56 mW Non-pipelined Rijndael AES Encryption JC in a 1.8V, 0.18 mm CMOS Technology. Electrical Engineering Department, University of California Los Angeles,Los Angeles, CA. 

[5] MROCZKOWSKI P. Implemetation of the block cipher Rijndael using Altera FPGA. Military University of Technology.