TD_SCDMA系统中TFCI译码在ZSP500 DSP内核上的实现
2007-10-30
作者:文 虹,申 敏,赵静娟
摘 要: 介绍一种由快速哈达码变换与超码译码结合实现的译码算法" title="译码算法">译码算法,该算法能降低TFCI的误码率,是一种简单有效的方法。在分析此译码算法的基础上,详细阐述了基于ZSP500 DSP内核的实现方法,并给出了程序实现的具体步骤。
关键词: TFCI ZSP500 快速哈达码变换
在TD_SCDMA系统中,传输格式组合指示TFCI(Transport Format Combination Indicatorl)描述了当前的传输格式组合。一个特定的TFCI值与一种特定的传输格式组合具有一一对应的关系。一旦检测到TFCI,就可知道各个传输信道的传输格式,包括传输块大小、编码类型等信息。因此TFCI是信道译码过程中非常重要的参数,保证了TFCI译码的正确性,才能保证信道译码的正确。
ZSP500 DSP内核是一种可编程的高性能处理器,不仅适用于数字信号处理,而且在图像处理、语音处理、通信等领域都得到了广泛应用。具有低成本、低功耗、高性能的处理能力,因此以其作为核心的智能控制器是智能化制造技术的发展方向。它的出现也使TFCI译码的实现变得更为方便。
1 TFCI译码算法设计
1.1 TFCI译码分析
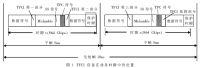
TFCI在各自物理信道的数据部分发送。编码后的TFCI符号在子帧内和数据块内均匀分布。已编码的TFCI符号平均地分配到两个子帧中相应的数据部分,紧挨着Midamble发送。所在位置如图1所示。
在3GPP标准中规定了三种不同的编码方案:极短TFCI(1~2位),较短TFCI(3~5位),较长TFCI(6~10位)。
最优的TFCI译码算法是穷举法,即将所有码字进行编码,与译码输出端的数据相比较,找出最相似的一个作为译码结果。该方法存在两大问题,一是在实际环境中,译码端输入的是经传输信道的数据,即加干扰后的数据,该数据与原始码字编码后的数据比较势必存在较大误码率;二是对较长TFCI,其所有码字的可能组合为210=1024,也就是说采用穷举法译码时,需存储1024个数据,这不仅影响运算速度,而且耗费存储空间。
对于较短TFCI采用一阶RM(Reed-Muller)编码,因此可采用FHT(快速哈达玛变换)直接译码[1]。关于RM的定义见参考文献[1]。较长TFCI采用了加掩码的一阶RM编码,是一种超码,即以一阶RM码为基础码集的陪集串。本文讨论的正是这种较长TFCI的译码算法,包括对双极性" title="双极性">双极性序列的变换、基础码集的译码以及去除掩码的处理过程。
1.2 TFCI译码
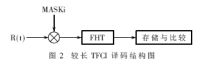
较长TFCI是采用基础码集加陪集串的编码方式构成的超码。其编码生成矩阵就是以一阶RM(1,6)为基础码集,加上16个掩码(包括全零向量)为陪集的编码方式。相应地,较长TFCI可采用超码译码法[2]。超码译码原理:第一步,在接收的双" title="的双">的双极性码字中依次乘双极性化后的掩码集,以此消除掩码;第二步,对消除掩码的码字采用基础码集的译码算法,在此即为一阶RM码的FHT;第三步,译出码字和相应的陪集表示,确定出最后的译码信息。所以较长TFCI译码主要分为消除掩码和基础码集译码两部分。其译码结构如图2所示。
1.2.1 消除掩码
陪集是编码生成矩阵的后四列组成的四维空间,即16个掩码(包括全零向量)为陪集所表示的陪集串序列。研究分析得知,对较长TFCI译码,首先要进行数据调整,即译码输入的原第31个数据调整为现第1个数据,原第32个数据调整为现第17个数据,原第l~l5个数据调整为现第2~16个数据,原第l6~30个数据调整为现第18~32个数据。然后对调整后的数据(即双极性序列r)进行去除掩码的处理。在去除掩码过程中,首先根据生成矩阵的后4列(基本掩码序列)的线性组合得出整个掩码集,然后将掩码集双极性化,最后用接收的双极性码字依次乘前面双极性化后的掩码集。这样,就完成了去除掩码的处理。
1.2.2 基础码集译码
由参考文献[2]可得出,TFCI编码的生成矩阵的前6列就是RM′(1,6)的变形。其变形顺序是将RM′(1,6)的倒数第二列放到第一列,倒数第一列放到第16列。所以,译码时必须变化输入序列,以适应译码矩阵。变换后得到的数据即双极性序列,需要进行FHT变换,然后再通过存储与比较进行译码,才能得到二进制信息序列m。
具体的软判决步骤如下:
(1)将译码输入端的双极性信息与双极性MASKi序列相乘,进行消掩处理,得到序列c(双极性形式);较短TFCI相当于MASKi为0。
(2)对序列c进行FHT变换,得到矩阵G;较短TFCI得到一个1*N的矩阵。
(3)在得到的矩阵G中寻找y的最大绝对值,得到最大值的行号" title="行号">行号p和列号q。
(4)较短TFCI译码结果为最大值的列号q的二进制形式。较长TFCI译码还要进行下列步骤:译码原信息的第一位根据y的正负进行判断。当y为正时,原信息的首位为0;当y为负时,原信息的首位为1。
(5)译码原信息的第2~6位为最大值列号q的二进制形式。
(6)译码原信息的第7~10位即最大值行号p的二进制形式。
2 TFCI译码实现流程设计
ZSP500内核以独有的高效面积、极低功耗、一流代码密度、实现四MAC的性能等优点成为高带宽3G频带处理和丰富多媒体应用的理想选择。其处理单元主要包括预取单元(PFU)、指令单元(ISU)、管线控制单元(PCU)、算术逻辑单元(ALU)等。结构框图如图3所示。
ZSP500强大而简练的指令集减少了开发时间,运行频率为250MHz。一个基于ZSP500的设备的处理能力可达1 000MIPS。ZSP500具有两个专有的地址生成单元(AGU),可以驱动各自专有的装载/存储端口,可在每个周期内完成两次装载两次存储,或一次装载一次存储。每个数据端口都是32位宽,因此每个周期内一共可以完成64位(4个字)的数据传输。另外PFU中还有一个跳转预测逻辑,能够提供zero-overhead循环,产生高效的跳转和调用。使用静态分组规则决定每个时钟周期" title="时钟周期">时钟周期执行的指令条数,在程序员逻辑上正确编写代码可保证多条指令并行执行,提高了效率。
较长TFCI译码实现时,可以从两方面简化和提高执行效率。
(1)采用FHT算法减少运算量
理论上,FHT将Hadamard矩阵分解为稀疏矩阵的乘积[3]。具体实现与FFT类似,采用蝶形变换,只是没有乘法运算。Hadamard变换是一个线性变换,其主要优点是所需空间小、运算速度快。在用ZSP实现时,只需存储一个一阶Hadamard矩阵,并且还可采用FHT算法减少运算量。由此看出,采用Hadamard变换对TFCI进行译码具有可行性。
FHT算法与FFT算法类似,采用蝶形变换。但是在ZSP500中没有提供类似TI C55xDSP中的ADDSUB指令,用一个机器时钟同时对两个寄存器进行加减。所以只能按下列代码分别执行,对执行效率有所影响。
FHT的关键代码:
ld r4,a0
ldu r5,a1,r8 !a1+r8
sub r7,r4,r5
add r6,r4,r5
stu r6,a0,1 !r6=add result
stu r7,a1,1 !r7=sub result
ZSP500中有两个16位的算术逻辑单元ALU,一个32位的乘累加单元MAU。在指令操作中先使用ALU,再使用MAU便可实现并行处理。另需注意,根据实际调试经验,发现sub、add两条指令是否能同时在一个时钟周期中执行,与调用顺序有关。若先调用sub就可以,反之则不行。考虑了以上因素,使指令开销大为节省。
(2)消除掩码的简化过程
较长TFCI译码需要消除掩码和寻找最大值行号与列号等步骤。消除掩码首先要列出所有可能的掩码输入,再让输入序列b与之相乘,即可消除掩码。根据此方法需要用到大量的乘法和加法运算,而且掩码矩阵固定不变。所以应事先做好一张消掩表,通过查表来完成。这样可以节省大量的时间和资源。
做一张消掩的矩阵表M(16×32);输入序列b中每个元素均需查表,看是否要取反(0表示要取反)。这样就完成了c=b×M运算。
ZSP500 的相邻通用寄存器可以连到一起,形成32位的寄存器,而且可以一次性读取32位。在读取掩码矩阵M时,利用ldd指令,可以提高处理效率。
消除掩码的关键代码:
ldu r0,a0,1 !r0=input
lddu r2,a1,2 !r3r2=M_tab element
bitt r3,15 !if M_tab =0, this input bit must neg
cexe (z,nu)
{
neg r0,r0
}
stu r0,a1,1
shll.e r2,1 !next M_tab element according next input bit
本文从以下几个方面对ZSP程序进行了优化: 第一,ZSP500是双40位ALU结构, 一个时钟周期内可以完成4次16位加法;第二,总线宽32位,一次可以读取或保存两个16位操作数; 第三,ZSP500具有数据处理和数据存取的并行处理能力。一条并行指令包括一次ALU/MAC操作和两次辅助操作;第四,合理安排执行顺序,尽量减小循环体内的指令数。
本文重点分析了TFCI译码的算法原理,并给出了ZSP的实现过程以及优化方法。TFCI是信道译码过程中非常重要的参数,只有在TFCI译码正确的前提下,才能保证信道译码的正确,因此本文对于实际的信道译码过程具有一定的实用价值。
参考文献
[1] COOKE B.Reed_Muller error correcting codes.MIT Undergraduate journal of mathematics.1999,1(6):21-26.
[2] 3GPP TS 25.222:Multiplexing and channel coding (TDD).Release 5,2004.
[3] ALEXANDER J.G,Richard D.van Nee.Efficient maximumlikelihood decodingof-ary modulated Reed-Muller codes [J].IEEE Communications letters,1998,2(5):134.136.
[4] ZSP500 Digital signal processor Core.LSI 公司,2003.