根据功率因数校正设备的基本电路分析混合功率因数校正的系统理论的正确性和他的实用性.根据Buck-boost 电路和Buck 电路作为基本变换器，可以得到如下图1A、2A、3A 所示的PFC 电路，如果考虑到隔离的需要，对应有如图1B、2B、3B 所示的PFC 电路。

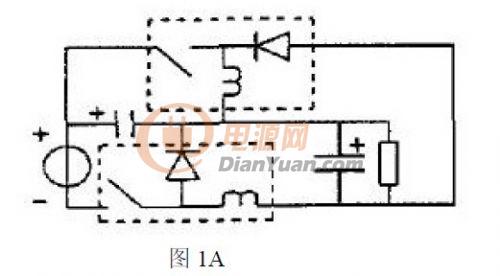
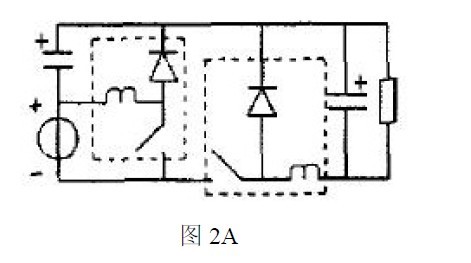
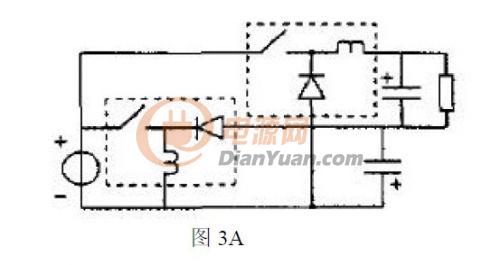
如果选择两个Buck-boost 电路作为基本变换器，同理可以得到3A 所示的电路。考虑到隔离的需要，有如图3B 所示的PFC 电路。

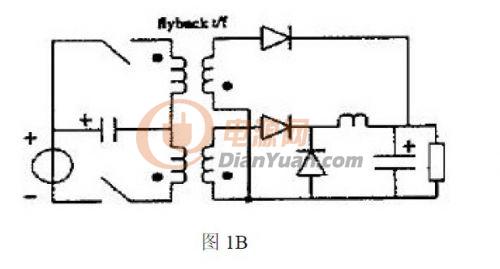
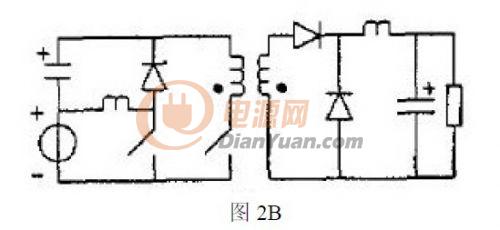
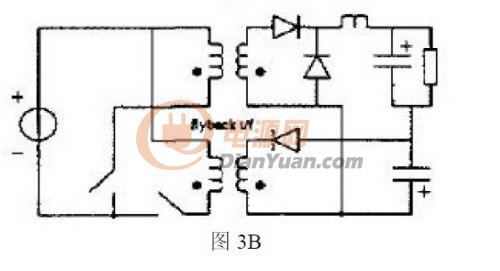
以上给出了一些基本拓扑的PFC 电路，下面将具体分析图1A 给出的电路。根据图1A，假设Buck-boost 和Buck 基本变换器都工作在CCM 状态下，本电路主要适用于中大功率的需求。

一．平均模型

假设电容电压是常数，输入电压为整流过的正弦波，如下所示

输入Buck 基本变换器的电压如下：

其中c V 是电容电压， m  是载波频率。假设输出校正良好，稳态时，Buck 变换器的输入电流如下：

其中， 0 P 为PFC 电路的输出功率。根据以上计算与推导，作出如图4 所示的平均模型，根据平均模型可知输入电流为L d i 1

和输入Buck 变换器的电流之和，其中1 d 是Buck-boost 变换器的占空比。

为了得到单位功率因数，可以得到以下等式：

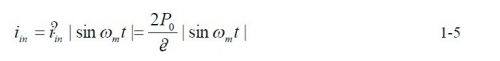
基于以上公式， 利用MathCad 仿真几个滚见参数波形。条件为

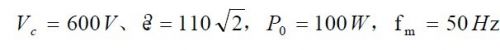
时，为了达到单位功率因素，几个主要电流、电压的波形如图5 所示：

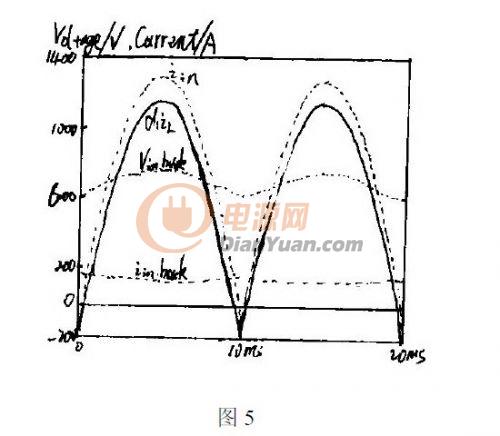
根据上图所示，为了达到单位功率因数的目的，在一段时间内L d i 1 为负值，所以可以使用一个允许能量双向流通的开关来替代Buck-boost 中的二极管。但实际上，即使任然采用二极管，仍能保持很高的功率因数，略小于1.而且，提高电容上的电压值，可降

低in bock i . ，从而保证功率因数一直维持在较高的水准上。

二．为了达到高功率因数，两个基本变换器分开控制。标记Buck-boost 变换器的占空比为

1 d ，Buck 变换器的占空比为d2 ，由此可以写出 d 2的表达式：

其中U 为输出直流电压.由式1-3、1-4 推得：

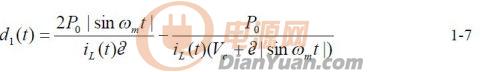
电感电流表达式如下：

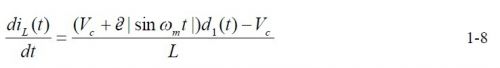
根据1-7、1-8 有：

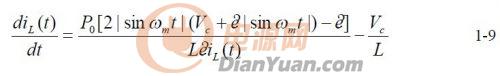
根据得出的1-9 式可以利用MathCad 的数值方法解出L i ，如图6 所示，再将L i 带入式1-7，可得出d1。

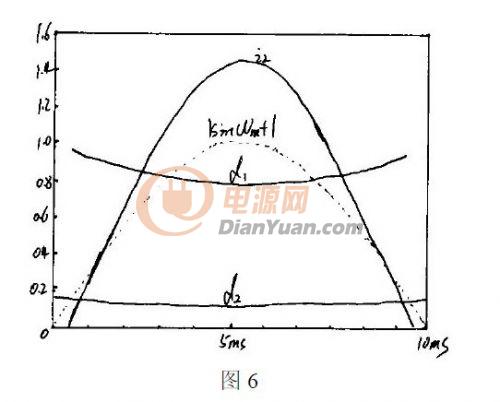
其中主电路波形接近过零点的附近， L i 无法求得数值解。在实际的应用上，需要分开控制Buck-boost 变换器和Buck（Flyback 考虑隔离）变换器。

1 对于Flyback 变换器，只需要简单的反馈控制环，但由于Flyback 变换器的输入电压为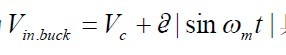

具有较大的波动，所以讲一个前馈环集合在反馈模型中，有利于快速调整输出。

2 为了取得较高的功率因数，前段的Buck-boost 变换器需由一个电流功率因数控制环来控制，从而有效的使得输入电流跟随输入电压。