常用数字通信信号调制方式分类的一种新方法
2008-12-15
作者:钟 骥, 周慧琴, 崔伟亮
摘 要: 提出了一种常用数字中频信号盲识别方法。该方法通过信号延迟复共轭相乘" title="共轭相乘">共轭相乘相位特征的分析,提出了两个新的分类特征参数" title="特征参数">特征参数,结合对信号非线性变换谱特征" title="谱特征">谱特征和信号包络的分析,应用层次结构判决树分类器实现了常见数字信号的自动识别。仿真结果表明,本文提出的分类算法计算简单,分类效果良好。
关键词: 调制识别; 共轭相乘; 谱特征
随着通信系统多样性和复杂性的增加,信号调制方式的自动识别已经成为通信信号分析领域里的一个重要组成部分。目前常用的通信信号的调制识别方法较多,如基于信号瞬时统计参数[1]和功率谱特征[2]的识别方法。在以信号的相位、频率、幅度等时域参数为特征参数的调制识别方法中,Nandi等[1]的研究工作最具代表性,并被广泛引用。Dubuc等[2]提出了一组实用的信号功率谱特征参数,但是参考文献[2]中并没有给出明确的定义。参考文献[3]提出了一种四阶累积量的方法对信号进行识别,但该算法的前提是信号达到完全的载波和时钟同步,这对非协作通信来说是难以实现的。
本文在对信号瞬时统计参数和信号非线性变换后的功率谱研究的基础上,提出了两个新的分类特征参数,改进了一个相关特征描述,这些参数具有运算复杂度低、抗噪声能力强、对调制参数稳健性强等特点。
1 调制信号特征分析和提取
本文主要讨论高斯信道下常用数字信号的识别,包括2FSK、4FSK、MSK、BPSK、QPSK、OQPSK、PI/4QPSK、8PSK" title="8PSK">8PSK
以及MQAM信号。
1.1 信号延迟复共轭相乘相位统计特征
对于MPSK信号,为讨论方便,首先给出其理想复信号模型:
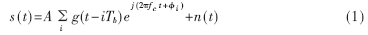
式中,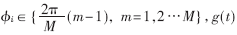 ,g(t)为脉冲成型滤波器。脉冲成型虽然抑制了码间干扰,但它使MPSK信号包络变得起伏。为了减小脉冲成型对信号特征提取的影响,可以使用幅度归一化对信号进行恒包络处理。设信号的瞬时幅度为|a(t)|,则在一个码元周期内调相信号经过恒包络处理的中频信号表达式为:
,g(t)为脉冲成型滤波器。脉冲成型虽然抑制了码间干扰,但它使MPSK信号包络变得起伏。为了减小脉冲成型对信号特征提取的影响,可以使用幅度归一化对信号进行恒包络处理。设信号的瞬时幅度为|a(t)|,则在一个码元周期内调相信号经过恒包络处理的中频信号表达式为:
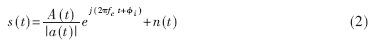
对信号进行延迟复共轭相乘:
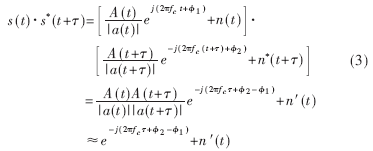
其中:φ1、φ2分别为原信号和延迟共轭信号的相位,且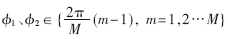

对于FSK信号,在一个码元周期内,其复信号表达式可表示为:
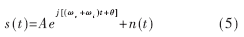
其中,θ为信号初始相位,θc+θi为MFSK信号的M个载波频率。同理,可求得其延迟相乘后的相位为:
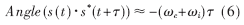
对由式(4)和式(6)得到的信号相位归一化后进行概率分布统计,统计等分数S=80,如图1和图2所示。从图 1容易看出各种调相信号的共轭相位概率统计分布图有着明显的差异:BPSK信号整体呈现细单峰状,带宽窄,且大部分统计等分点聚集在底部;QPSK信号上半部分表现为细单峰状,下半部分向两侧展开;PI/4QPSK呈现双峰状;8PSK表现为单峰状,但带宽比BPSK信号宽且统计等分点分布较为均匀。
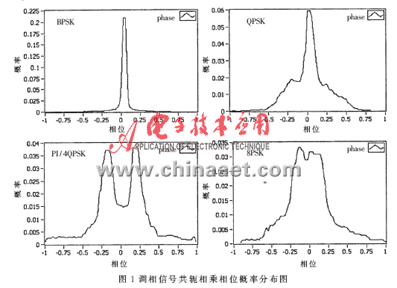
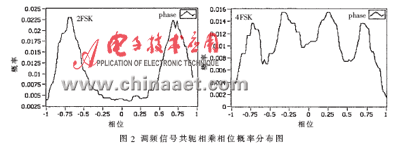
从图2可以看出调频信号的共轭相位概率分布图呈现多峰状,峰值数与调频信号的阶数有关,反应了调频信号频率的分布状况。
1.1.1 峰谷点重比FQ参数
本文首次提出该参数,用于BPSK信号与QPSK、PI/4QPSK、8PSK三种信号的区分。如图3所示为BPSK和 
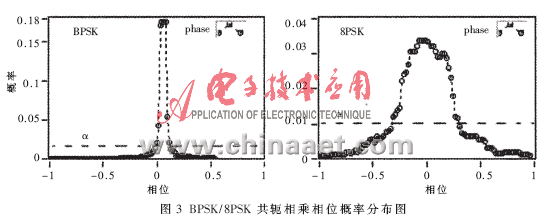
式中,P(si)为概率分布图中每点所代表的分布概率,N[P(si)<α]为出现概率小于α的统计点数。
FQ参数反映了概率分布图中各概率点的聚集程度,由前面分析知道,BPSK信号概率分布图呈窄单峰状,且大部分统计点聚集在底部,所以它的FQ值相对较大;而QPSK、PI/4QPSK、8PSK信号的概率分布图中各统计点相对分散,它们的FQ值较小,所以FQ参数可以用来区分BPSK信号和QPSK、8PSK、PI/4QPSK三类信号。
1.1.2 峰谷带宽比FB参数
本文首次提出使用峰谷带宽比FB参数区分用于QPSK和8PSK、PI/4QPSK两类信号。图4为QPSK/8PSK共轭相乘相位概率分布图。
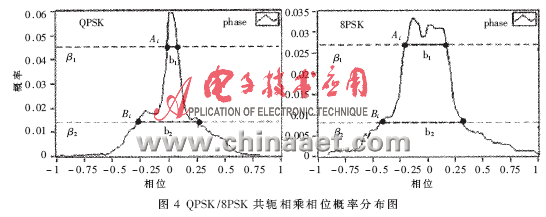
令β1=max[P(si)]·η,β2=max[P(si)]·(1-η)
设门限β1与概率分布图的交点坐标为Ai(αi,β1),门限β2与概率分布图的交点坐标为Bi(bi,β2)。定义:
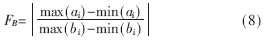
其中,η为比列因子,且0<η<1。
FB参数反映了信号概率分布图波形带宽的变化程度。前面已经分析过,QPSK信号概率分布图带宽上半部分窄,下半部分宽,其FB值相对较小;而8PSK和PI/4QPSK信号带宽变化较小,其FB值相对较大,所以可以依据FB参数来区分QPSK和8PSK、PI/4QPSK两类信号。
1.2 信号延迟复共轭相乘相位谱特征
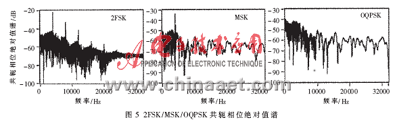
对由公式(4)和公式(6)得到的信号相位进行均值归一化后取其绝对值谱,如图 5所示为2FSK、MSK、OQPSK信号的共轭相位绝对值谱。可以看出,2FSK和MSK信号在码元速率附近存在单频分量,而OQPSK则无单频分量(对其它的调频类信号仿真也能得到类似的结果)。因此,可以通过检测单频分量是否存在来区分OQPSK信号和调频类信号。
1.3 反映信号包络变化的改进描述Ap参数
对于不同调制方式的信号,其瞬时幅度也体现出一定的差异。因此,对信号瞬时幅度参量的提取可以作为分类信号的一个重要特征。参考文献[4]提出了用R参数来区分恒包络信号和非恒包络信号,并取得了较好的效果,但是它没有考虑到脉冲成型对信号包络的影响,对调相类信号和幅相类信号的区分性能欠佳。本文受其启发,对信号的瞬时幅度经过预处理后,将其表现为极坐标的形式,如图 6、图 7所示。从图中可以看出各类信号瞬时幅度的变化规律:


·以2FSK为代表的恒包络信号,其瞬时幅度的样点绝大部分散布在以r为半径的圆周附近,少量样点出现在以r/h为半径的同心圆内(h≥2且h∈r);
·以QPSK为代表的准恒包络信号(受脉冲成型的影响),其瞬时幅度的样点部分散布在以r为半径的圆周上,少部分散布在以r/h为半径的同心圆内;
·以16QAM为代表的非恒包络信号,由于其幅度调制和相位跳转状态较多的原因,其瞬时幅度的样点在以r为半径的圆内分布相对较均匀。
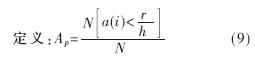
其中,N为总样点数,a(i)为第i个样点的样点值。Ap参数反映了信号包络的变化程度,由前面分析知道,恒包络信号由于其样点多数分布在圆周附近,故其Ap值较小;准恒包络信号由于有部分样点散布在圆心附近,其Ap值较恒包络信号大;非恒包络信号样点在圆内分布均匀,其Ap值较大,所以可以通过Ap参数来区分这三类信号。
2 算法性能分析与仿真
实验一 BPSK、QPSK、PI/4QPSK、8PSK信号FQ和FB参量取值随信噪比" title="信噪比">信噪比变化情况
仿真中,调制信号符号速率、载波频率、采样率分别为4 000Hz、8 000Hz、64 000Hz;脉冲成型采用根方升余弦滤波器,成型系数为0.5,各调制方式在同一信噪比下仿真500次,每次仿真数据长度为8 192个样点,仿真曲线如图 8所示。
从图中可以看出,FQ和FB参量的取值受信噪比的影响较小,具有较好的稳健性。BPSK信号FQ参数与其他三类调相信号有较大差异,且取值随着信噪比的增加趋于稳定,这与前面的特征分析相吻合,故FQ参数可用于在较低信噪比下区分出BPSK信号; QPSK信号的FB参数随着信噪比的增加逐渐减小,而其它三类调相信号的FB参数随着信噪比的增加逐渐递增,这样,低信噪比的分类阈值也同样适合于高信噪比的情况,故FB参数可以较好地区分出QPSK信号。
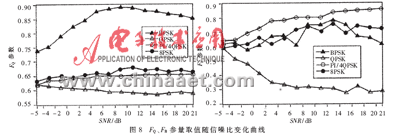
实验二 2FSK、4FSK、MSK、BPSK、QPSK、OQPSK、PI/4QPSK、8PSK、16QAM、64QAM信号Ap参量取值随信噪比变化情况
仿真中,2FSK信号调制指数为0.6,4FSK信号调制指数为1.2,其他条件同实验一。各调制方式在同一信噪比下仿真500次,仿真曲线如图9所示。图中结果表明,Ap参量较好地反映了信号瞬时幅度的变化情况,当信噪比大于4dB时,各调制信号的Ap参量取值趋于稳定,幅相类信号(16QAM、64QAM)、调相类信号(BPSK、QPSK、PI/4QPSK、8PSK)以及调频类信号(2FSK、4FSK、MSK)之间都有较明显的差异,其中OQPSK信号由于调制时正交分量和同相分量相对延迟了半个码元间隔,减小了包络的起伏,使得其分布特征与调频类信号相似。在信噪比大于5dB时,Ap参量可以对上述的三类信号进行有效区分。

实验三 信号分类性能测试
实验采用蒙特卡罗统计法,在信噪比为0dB、5dB、10dB和15dB的条件下分别随机产生上述各类信号,各信噪比下分别进行10 000次仿真测试,其他条件同实验二,采用图10所示的识别流程对随机产生的信号进行调制方式识别,每次识别数据长度为8 192个样点,识别结果见表 1,信号识别流程中的C参量和F参量请参考文献[5]。可以看出,在低信噪比时,对4FSK 和PI/4QPSK信号的识别性能较差,这是由于在信噪比较低时特征所呈现出来的谱峰数被噪声淹没所导致的;BPSK、QPSK信号的识别效果较好,在0dB时的识别率仍大于80%,这与实验一的结果吻合;随着信噪比的提高,各信号的识别性能得以改善,当信噪比为10dB时,信号的正确识别率均大于90%。


文章提取了两个新的分类特征参数,并结合非线性变换后的谱特征和瞬时统计参数实现了常用数字信号的识别。本文算法结构清晰、计算简便,在较低信噪比条件下具有较高的识别率,易于实现,具有一定的实用价值。
参考文献
[1] NANDI A K,AZZOUZ E E.Algorithms for automatic modulation recognition of communication signals[J].IEEE Trans Comm,1998,46(4):431-436.
[2] DUBUC C, BOUDREAU D. An automatic modulation recognition algorithm for spectrum monitoring applications[A]. In Proc of IEEE International Conference ON Communication(ICC’99)[C].Vancouver,Canada,1999.732-736.
[3] 陈卫东,杨绍全,董春曦,等.多径信道中MPSK信号的调制识别算法[J].通信学报,2002,23(6):14-21.
[4] CHAN Y T, GANDOIS L G. Identification of the modulation type of a signal [J]. IEEE Signal Processing,1989,16: 149-154.
[5] 范海波,杨志俊,曹志刚.卫星通信常用调制方式的自动识别[J]. 通信学报,2004,25(1):140-149.

