摘  要： 提出在支持向量机回归预测中采用粒子群算法优化参数和主成分析降维的方法，通过算例分析表明，此法能够显著提高预测的精度。
关键词： 支持向量机；粒子群算法；主成分析法；预测

    预测是国家、企业等组织制定政策和计划的主要依据，因而预测的准确度是政策与计划制定是否科学的前提。预测的方法有传统的多元回归预测，以及近几年来发展起来的人工神经网络预测[1]、灰色预测[2]。多元回归预测模型简单、易用性强，但难以处理高维、非线性模式；人工神经网络虽然能够较好地解决高维非线性预测的难题，但它需要大量的训练样本，且泛化能力不强，所以当可得到的预测样本是小样本，或者获得大量样本的成本很高时，就难免影响其实用性和经济性；灰色预测虽具有短期预测能力强，可检验等优点，但其长期预测能力较差。Vapnik等人提出的支持向量机[3-4]是在统计学习理论基础上发展起来的一种新的机器学习算法，是目前针对小样本统计和预测学习的最佳理论，支持向量机具有完美的数学形式、直观的几何解释和良好的泛化性能，解决了模型选择与欠学习、过学习及非线性等问题，克服了收敛速度慢，易陷入局部最优解等缺点，因此支持向量机在分类和回归中均表现出优越的性能。

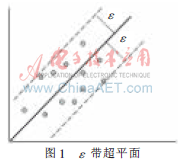
射函数。核函数的作用是当样本点在原空间线性不可分时，可以通过映射函数映射到高维空间，从而达到线性可分的目的，但实际应用中映射函数的显式表达式很难找到，观察式(2)~式(4)中只用到了映射在高维空间的点积，而核函数的特点就是能使变量在低维空间核函数值等于其映射到高维空间的点积值，从而实现不需要知道显式映射函数达到向高维空间映射的目的。任何满足Mercer 条件的函数均可作为核函数。
2 粒子群算法基本原理
    微粒群算法最早是在1995年由美国社会心理学家Kennedy和Russell[6]共同提出，其基本思想是受鸟群觅食行为的启发而形成的。PSO算法把优化问题的解看作是D维空间中一个没有体积没有质量的飞行粒子，所有的粒子都有一个被优化目标函数决定的适应度值，而速度决定每个粒子的飞行方向和距离，粒子根据自己先前达到的最优位置和整个群体达到的最优位置来更新自己的位置和速度，从而向全局最优位置聚集。粒子根据以下公式来更新自己的速度和位置：

4 应用实例
    试验从UCI上选取美国波斯顿地区1993年城镇住房数据作为试验数据[9]。试验步骤如下：
    (1)应用主成分析法降维
    由于统计软件SPSS提供了主成份分析功能，而且具有采用交互式、图形化操作界面、结果图形化输出、直观性强等优点，故本文采用SPSS16.0作为降维工具，表1为最大方差旋转后的因子载荷图，从表中可以看出，7个主成份都有很好的解释意义(载荷绝对值>0.5，说明变量与主成份存在相关性)。主成份1为城镇生活环境，主成份2为治安环境，主成份3为人口密度，主成份4为人口层次，主成份5为是否有河流，主成份6为商业环境，主成份7为教育发展水平。

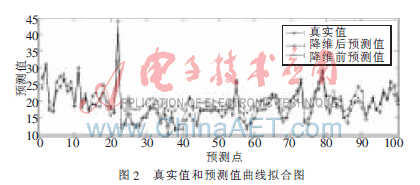
    本文把量子群优化算法和主成分析降维的方法应用于支持向量机的回归预测中，试验结果表明此法能显著提高支持向量机的预测精度，同时也表明了支持向量机在非线性、高维模式下的良好预测性能。
参考文献
[1] 阎平凡，张长水.人工神经网络与模拟进化计算[M].北京：清华大学出版社，2006.
[2] 韦康南，姚立纲等.基于灰色理论的产品寿命预测研究[J].计算机集成制造系统，2005(10)：1491-1495.
[3] VAPNIK V N. The nature of statistic learning theory[M].New York： Springer， 2005.
[4] VAPNIK V N. Estimation of dependencies based on empiric[M]. Berlin Springer-Verlag， 2003.
[5] 邓乃扬，田英杰. 数据挖掘中的新方法-支持向量机[M].北京：科学出版社，2004.
[6] KENNEDY J， EBERHART R. Particle swarm optimizat[A].Proc IEEE Int  Conf. on Neural[C]. Perth， 1995. 1942-1948.
[7] CLERK， M. The swarm and the queen： Towards a deterministic and adaptive particle swarm optimization[A].1951-1957. 1990. Proc. CEC 1999.
[8] 林海明.对主成分分析法运用中的十个问题的解析[J].统计与决策(理论版)，2007(8)：16-18.
[9] http：//archive.ics.uci.edu/ml/index.html 1993.07.