逐次逼近型ADC是采样速率低于5 MS/s的中高分辨率应用的常见结构，SAR ADC的分辨率一般为8~16位，具有低功耗、小尺寸等特点，因此具有较宽的应用范围，如：便携式仪器电池供电仪表、工业控制和数据/信号采集器等[1]。
    在现有工艺水平下，由于受电容失配、系统失调以及噪声等因素的限制，采用电荷再分配结构的SAR ADC能够达到的最高精度被限制在12位左右[2]。因此，高精度ADC设计必须依靠校准技术。一般校准技术有两类：模拟校准技术是在模拟领域把相关的量调整到正常数值或者利用激光对芯片元件进行修正，但这种技术成本高，且容易受到封装时机械应力的影响；还有一种数字校准技术，通过把电路中失配误差等影响在数字领域描述，然后在数字领域对输出代码进行调整，而不关心模拟领域的物理量数值[3]。数字校准是现行校准技术的主流。
    提出一种基于二进制加权电容阵列DAC的数字校准算法，用一个低精度的DAC表示各个待校准电容的失配误差值，然后在AD转换过程中，将相应的误差电压加载到电容阵列中，实现对电容网络的校准。
1 SAR ADC内核原理
    SAR ADC的基本结构由比较器、DAC、SAR逻辑控制电路组成，如图1所示。

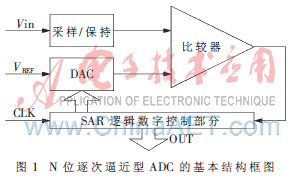
    基本工作过程：首先模拟输入Vin被采样保持，送入比较器的一端， N位SAR寄存器的初始值为中间值（即100……00），DAC将该值转换为对应模拟量VDAC=VREF/2(VREF是ADC的基准电压)。比较器开始比较Vin与VDAC的大小。若Vin>VDAC，则比较器输出1，SAR寄存器的最高位保持，次高位预置为1；反之，比较器输出0，SAR寄存器的最高位为0，次高位预置为1，ADC进行下一次比较。这样反复逐次比较直到SAR寄存器的最低位，寄存器中保存的N位数字量就是ADC的转换结果。
2 数字校准算法
    数字校准算法的基本思想是在ADC正常使用前，先计算电容失配等的一些非线性误差，把误差相应地在数字领域用校准码形式描述，并在正常工作过程中把这些校准码加载到电路中进行误差校准，从而达到校准失配的目的。校准码的产生和使用有不同的算法[4，5]，本文设计了一种从低位到高位电容依次校准的思想。
2.1 校准码产生的算法原理说明
    本设计中采用对称的分段电容结构，如图2。对称差分结构使得比较器输入负载相等，消除比较器的共模噪声，提高信噪比；分段电容阵列采用高位与低位通过过渡电容耦合的结构，保证了MSB的高精度以及LSB的单调性。N（N=M+K）位的SAR ADC由左右侧差分结构的高M位DAC以及左侧低K位的DAC构成，右侧低K位则用于校准电容阵列的失配误差。

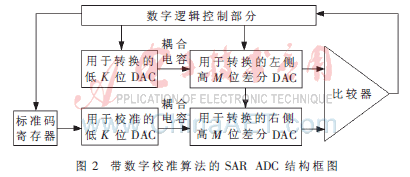
    产生校准码的工作过程中，设置两种电容阵列工作状态：Φ1工作状态下接入一组电容，并将左右侧电容阵列的输出与比较器的输入端断开（比较器两端输入均为0），同时电容阵列输出端接共模电平VCM；Φ2工作状态下接入另一组电容，输出接比较器两端的输入端进行比较。通过两种工作时序的切换，根据电荷守恒以及电荷重分配原理，待校准电容之间的失配误差可以通过右侧低K位的校准电容阵列表示出来。
    下面以高位电容为例，分析校准码产生原理细节。图3为在两个不同的工作状态下左侧电容阵列的等效模型。

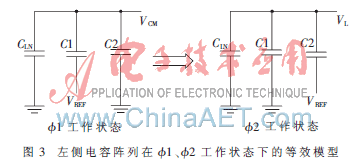
    图3中，CLN表示左侧电容阵列中除了C1、C2电容外的所有电容之和，C1表示已经校准的所有电容之和，C2表示目前待校准的电容，且C1、C2为相邻的两组电容，设CT表示左侧电容阵列总电容值，即有CLN+C1+C2=CT。VL端接入比较器的一个输入端，根据Φ1、Φ2两种工作状态下的电荷守恒原理，则有：
 

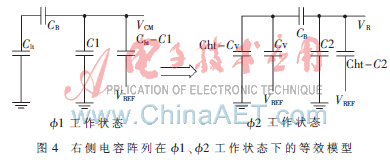
式(4)中，C1是已校准电容，且C2与C1之间有相互联系的权重关系，而C2与C1之间的失配误差可以通过CV描述出来。CV的值对应右侧低K位电容阵列的开关二进制值，即将电容失配误差的影响通过数字域描述出来，并在正常转换过程中，将这些误差通过相应的处理后加载在电路中，实现校准误差的效果。
2.2 SAR ADC校准算法的实现
    假设单位电容的失配误差为?驻，通过对应位电容数量的加和，可以近似模拟高位电容误差的统计分布情况。当每位电容的统计误差与其对应的权重(2n)乘积超过单位权值时，需要考虑对此位进行校准。
    现假设需要校准的最低位电容CL1为左侧低K位电容阵列中的某电容。将CL1低一位的电容C0视为基准电容值，高位电容则需要依次校准为2i×C0，以达到相互匹配的关系。首先需要用右侧低位校准电容阵列表示出基准电容C0的大小。在Φ1工作状态，左右侧电容阵列均不接入电容，输出接共模电平。Φ2工作状态，左侧电容阵列接入C0，同时右侧低位校准电容阵列接入可变的Cv0电容，观察比较器的输出，当比较器输出发生跳变时，有：
 
    Calib集合保存的是对应位电容的校准码值，在正常的SAR ADC模数转化过程中，加载到右侧低位的校准电容阵列中，与对应待校准电容的共同作用下，起到校准电容失配误差的效果。
3 系统行为级仿真及结果分析
    设置单位电容的失配误差为0.5%，建立带有统计分布失配误差的14 bit电容阵列模型。由于本次的系统行为级仿真是为了验证校准算法的正确性及有效性，因此，设计比较器为理想的比较器，可以实现无限精度的比较。
    系统级仿真内容包括采用码密度直方图方式仿真微分非线性（DNL）和积分非线性（INL）等常规静态参数，并采用FFT法进行频谱分析，仿真信噪比、信噪失真比和有效位数等动态参数[6]。
    进行静态参数仿真时，满足0.3LSB精度、95%置信度，仿真点数设置为220个。
    对于ADC的频谱分析，设置采样频率fs为200 kHz，采样点数为N为8 192个点，采样的周期数M为129个。
    SAR ADC在未进行数字校准时，由于电容之间的失配误差导致ADC非线性，引起频谱的失真，在频谱图上表现出明显的谐波，造成信噪比以及有效位数都比较低。从仿真结果(见图5、图6)可以看出信号噪声失真比SNDR为72.9 dB，有效位数仅为11.82 bit。静态参数INL、DNL分别为2.86 LSB、5.01 LSB，说明存在严重的失码。

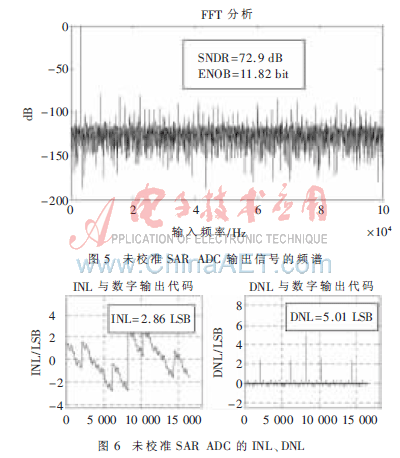
    在相同采样频率及输入信号的情况下，对SAR ADC进行数字校准。从仿真结果可以看出(见图7、图8)，校准后，ADC的非线性有了明显改善，SNDR有明显的提高，为85.1 dB，有效位数为13.85 bit，接近理想的转换位数。静态参数INL、DNL分别为0.25 LSB、0.26 LSB。

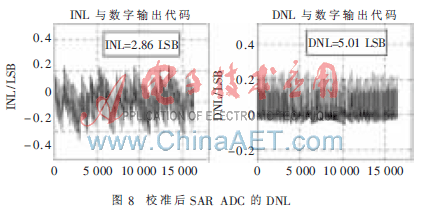
    本文详细介绍了一种基于二进制加权电容阵列SAR ADC的数字校准算法。该算法通过利用两种不同工作状态下电容阵列电荷守恒以及电荷重分配原理，实现由低位到高位依次校准电容的目的，大大改善了整体SAR ADC由电容失配引起的非线性。通过对实际14 bit SAR ADC系统级的仿真可以看到，在加入校准算法后，ADC的信噪比以及有效位数得到明显的提高，非线性失真很大程度上得到了抑制，即验证了本校准算法的正确性和有效性，为高精度SAR ADC的设计提供了有效而且易于实现的数字校准算法。
参考文献
[1] 魏智.解析逐次逼近ADC[J].国外电子元器件，2003(2)：72-74.
[2] 周文婷，李章全．SAR A/D转换器中电容失配问题的分析[J]．微电子学，2007，37(2)：199-203 .
[3] 戴澜，周玉梅，胡晓宇，等．一种流水线ADC数字校准算法实现[J]．半导体学报，2008，29(5)：993-997.
[4] LEE H S.Self-calibration technique for A/D converters[J].  IEEE Transactions on Circuits and Systems，1983，30(3)：188-190.
[5] 乔高帅，戴庆元，孙磊，等.基于16位SAR模数转换器的误差校准方法[J].微纳电子技术，2009，46(10)：636-639.
[6] 王卫江，陶然.高速ADC的性能测试[J].电子技术应用，2004，30(2)：33-34.