摘  要: 介绍一种用MCS-51单片机直接产生FSK信号的方法：首先采用PWM调制方法产生正弦波" title="正弦波">正弦波信号，再根据串行口输出的高、低电平产生FSK信号。

　　关键词: 频移键控(FSK) 脉冲宽度调制(PWM)  机器周期" title="机器周期">机器周期  连续相位

　　在遥测遥控系统中，数据的调制和解调是经常遇到的问题。一些自报测站不接收远方的遥控命令，只是定时采集参数或在参数变化时采集，并自动将采集的参数发往监控中心。这些遥测站不一定包含解调功能，但信号调制是遥测站的必要功能。

　　在水情自动测报系统中，数据传输大量采用超短波无线电台。用模拟电台传输数字信号时，调制方法多采用FSK。水情自动测报规范推荐的标准为CCITT V.21，即:数据串行速率为300波特率，数据电平“1”调制频率为980Hz，数据电平“0”调制频率为1180Hz。

　　调制解调的通常方法是采用专用的调制解调接口芯片，如MC145442、XR2211、XR2206等。采用专用调制解调接口芯片不仅增加了设备成本，而且芯片质量直接影响测控设备的性能。就一般而言，设备中的元器件越多，设备的可靠性越低。因此，在满足系统功能的前提下，应尽可能减少设备中元器件的品种和数量。遥测遥控设备的信号调制解调是非常重要的环节，如果能够减少或省去调制解调专用接口芯片，将对提高设备的稳定性和可靠性大有好处。

　　目前，几乎所有的遥测设备都使用单片机，其中MCS-51系列单片机又占了很大比例。本文将以MCS-51单片机为例，说明利用单片机的软件调制产生标准的FSK信号。

1 正弦波的调制

　　单片机的输出接口一般只能输出逻辑“0、1”，即0、Vcc两种电位。要想得到FSK信号，首先要得到正弦波信号，再根据串行数据的变化产生FSK信号。

　　从单片机获得正弦波，最简单的方法就是利用方波滤波得到正弦波。由于单片机的脉冲输出只有正电平，没有负电平，方波负半周，单片机无法产生负脉冲。因此产生的信号波形应该叠加一个直流正电平，使信号波形完全处在正电平一侧。如图1所示。

　　然而，方波是由基波和一系列高次谐波组成。如果图1可以用函数f(x)表示，将函数f(x)进行傅里叶级数展开可以得到:

　　从式(1)可以看出，接近基波的谐波成分比重较大。采用低通滤波器滤波时，接近基波的谐波成分难以滤去，为了减小波形的失真往往需要增大滤波的强度，这样在减小波形失真的同时，基波的损失也随之增大。

　　如果采用正弦波脉宽" title="脉宽">脉宽调制(PWM)可以得到比较满意的结果。PWM调制可以利用“0、1”变化的脉冲信号调制出模拟信号。

　　在计算机中，对连续曲线进行数字化处理时，通常将连续曲线用阶梯图形表示，当阶梯的步长足够小的时候，所表示的曲线被认为是精确的。图2的上图表示了不同时段内，电压的不同阶梯。

　　但是单片机输出接口不能产生变化的电平，即不能产生如图2所示的电压阶梯，所能做的只能是“0、1”电平的时间变化，即PWM调制。

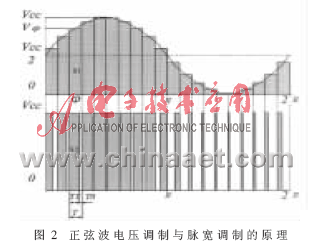
　　所谓正弦波PWM调制就是调制出的波形尽可能接近正弦波，也就是傅里叶级数中的基波比重尽可能大，高次谐波的比重尽可能小。对于图2来说，在调制过程中使每个时段内下图的阴影面积与上图对应部分的阴影面积相等。在用PWM调制正弦波时，要求时段的分割是偶数，因为正弦波图形是一种对称图形。

　　对于一个周期函数可以进行傅里叶级数的展开，级数的一般表达式为:

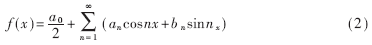
　　当按上述方法进行PWM调制时，图2下图函数傅里叶级数的an均为0，当n为偶数时，b_n也为0。所以正弦波PWM调制的傅里叶级数为:

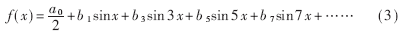
　　根据阶梯图形表示连续曲线时，阶梯越细图形越精确的原理，认为用PWM调制正弦波时，时段分割越多，调制出的正弦波越精确。如果不考虑级数中的直流成分，可以得到不同时段的谐波系数，如表1所示。

　　从表1可以看出，谐波系数随着谐波次数的增加逐渐减小，但在n=K-1处系数会突然增大，之后又逐渐减小。而这种突然增大的比值随着时段分割数的增加总体呈下降趋势。

　　另一方面，突然增大的比值，随着时段分割数的增加而向高次谐波方向移动。对这种远离基波的高次谐波，只要采用低通滤波器就能很容易将其去除，我们所关心的是如何尽可能减小基波附近谐波的系数。

　　从表1可以看出，随着时段分割数的增加，离基波较近的谐波系数也呈下降趋势。所以通过对时段的细分，信号的高次谐波，特别是接近基波的谐波成分会进一步减少。

2 信号输出

　　由于采用了正弦波PWM调制，单片机输出信号只要经过简单的低通滤波器就可以得到平滑的正弦波信号。图3中的74HC04是CMOS反相器，这里它起缓冲驱动作用。

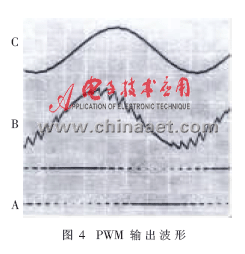
    因为单片机的P1～P3口是准双向口。作为输出口时低电平有一定的吸收电流能力，但高电平" title="高电平">高电平输出电流的能力很小，这就使输出信号的开关特性有较大差异。而CMOS反相器的输出采用P沟道和N沟道MOS管构成的对称互补结构，使输出信号的“0、1”有相同的开关特性，能保证低电平的吸收电流和高电平的输出电流相同。图3中R₁、R₂为1kΩ的电阻，C₁、C₂、C3为0.1μF的独石电容。当时段分割为20，正弦波信号频率为1180Hz时，图3中A、B、C三个端口的输出波形如图4所示。

3 CPFSK调制

　　软件调制是将正弦波分为若干个时段，并计算出每个时段内高电平和低电平所占用的时间，这些时间在单片机中用软件延时实现。

　　为了叙述方便，首先定义几个符号:

　　φ——软件调制所在的相位;

　　T——相位角为φ时对应时段的机器周期总和;

　　T₁——相位角为φ时对应时段的高电平机器周期;

　　T₀——相位角为φ时对应时段的低电平机器周期;

　　T₁₁₈₀——相位角为φ时频率为1180Hz正弦波对应时段的机器周期总和;

　　T₉₈₀——相位角为φ时频率为980Hz正弦波对应时段的机器周期总和。

　　根据图2中面积相等，即S1=S2的要求可以得到:

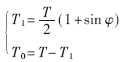
　　如果单片机的晶振" title="晶振">晶振频率为11.0592MHz，完成频率为980Hz的正弦波调制需要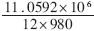=940个机器周期，完成频率为1180Hz的正弦波调制需要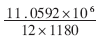=781个机器周期。

　　20等分能够将940整除，得到每个时段的机器周期数T₉₈₀=47。但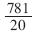=39余1，如果将余数1丢掉，就会造成频率为1180Hz的正弦波频率误差变大。实际编程时可以将余数1插补在20个时段中的某个时段中，也就是19个时段为T₁₁₈₀=39个机器周期，1个时段为T₁₁₈₀=40个机器周期。T0和T1的计算如表2所示。

　　如果波形调制是单一频率的，调制程序可以非常简单，只要编制顺序程序就可以了。如果波形调制的频率是变化的，就需要根据串行数据“0”或“1”的变化来改变每个时段的延时时间。在MCS-51单片机中，串行数据流是由软件设置，硬件自动产生，由TXD自动发出的。TXD的高低电平变化可以通过单片机的程序测得。根据这一特性，可以通过不断检测TXD的高低电平变化来决定每个时段的延时时间。程序流程如图5所示。

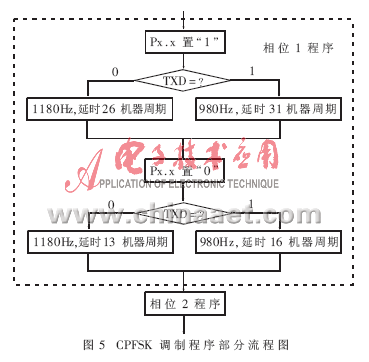
　　从流程图5可以看出，在每个相位中，单片机将Px.x置“1”或置“0”后都要判断TXD的电平，以确定相应延时的机器周期数。在某个相位TXD电平开始改变时，程序就从这个相位改变脉冲的延时时间，而程序中相位执行的次序并不改变。所以在TXD的电平改变时，两种频率的正弦波信号在同一个相位上交接。因此，FSK调制相位是连续的，见图6。

　　编程时必须注意，程序不论走哪条分支，所用的机器周期数都必须跟踪计算，最终所用的机器周期数必须符合表2的要求。另外，在进行FSK调制前应该增加一定长度的980Hz 的载波信号(PWM980)作为前导码信号。在数据发送完之后还应该增加一定长度的PWM980作为停止位，因为单片机的TI标志出现在数据帧停止位的前沿。

4 波形的优化

　　图4中B端的波形也就是带有锯齿的正弦波，是PWM调制经一阶滤波后产生的波形。该波形已具有了正弦波的大致形状，但锯齿也很明显，它和图2的阶梯波有些相似。通过前面的分析和表1的比较知道，增加PWM调制的时段分割数可以提高正弦波的波形精确度。

　　对于时段分割应该选择一个适当的数字。分割太粗，波形的失真就会严重，给滤波带来困难;分割过细会增加程序所占的空间。另一方面，时段的分割也不可能无限加大，因为采用软件延时时，延时时间的最高分辨率为1个机器周期。从表2也可以看到，在第4和第6时段出现了最小脉宽为1个机器周期的情况，而在第5时段甚至出现了只有高电平没有低电平的现象。如果继续细分时段，将会出现更多的只有一种电平的脉宽而另一种电平脉宽长度为0的现象。按上述等分时段的方法，如果不提高单片机的晶振频率，20个时段的分割已达到极限。所以不能单纯地采用细分时段的方法来提高波形的精度。

　　从图4中带有锯齿的正弦波可以看出，锯齿的大小在整个波形上不是处处相等的，波峰左侧的锯齿要比右侧的锯齿小得多。

　　从图2的阶梯波形可以看出，当阶梯波的精度最高时，应该是电压的步长或时间的步长之一为最小，而不是电压步长与时间步长之和为最小，当然更不能是电压或时间的任何步长为0。同样，用脉宽波表示正弦波时，精度最高的表示方法应该是“0、1”之一的脉宽为最小，而不一定是“0、1”脉宽之和为最小，也不能是“0、1”之一的脉宽为0。

　　从图4中可以看出，波峰的左侧恰好是“0、1”之一的脉宽较小的地方，这里的锯齿较小。波峰的右侧是“0、1”脉宽比较平均的地方，这里的锯齿较大。

　　根据上述分析知道，要想提高波形的精度就要对时段细分，细分的原则就是“0、1”之一的脉宽为最小。这样每个时段就不会是均等的。在单片机中，脉冲的延时的最小时间是一个机器周期。如果PWM调制的是单一频率的正弦波，“0、1”之一的最小脉宽就是一个机器周期。但是在进行FSK调制时，由于在执行每个脉宽延时时要对TXD的电平进行判断，一个机器周期显然不够用。如果某个时段的高电平脉宽T_1180(H)=3，T_980(H)=4，根据图5的程序流程，具体的程序是:

　　从上面程序可以看出，如果某个时段T_1180(X)≠T_980(X)，T_1180(X)的最小值为3个机器周期，T_980(X)的值则是根据T_1180(X)所在相位做相应的增加。当然，当T_1180(X)=T_980(X)时，T_1180(X)和T_980(X)的最小值可以是1个机器周期。

　　单片机的晶振频率为11.0592MHz，采用这种方式调制，时段分割为52个，调制的结果如图7所示。比较图7与图4可以发现，波峰左侧变化不大，波峰右侧的锯齿却大大减小了，整个波形的精度有了很大提高。

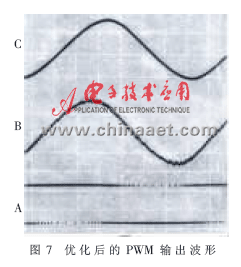
　　采用单片机的输出接口直接调制产生CPFSK信号，充分利用了单片机的资源，节省了元器件，同时也提高了信号频率的稳定性和灵活性。因为FSK的频率只与单片机的晶振和软件有关，晶振的频率是非常稳定的。采用软件编程调制可以根据信号的需要进行灵活多样的变化，而不用担心专用元器件的供货问题和元器件的质量问题。该调制方式已在全国许多地区的水情自动测报系统中应用，运行结果是非常理想的。

参考文献

1 ALAN V.OPPENHEIM  SIGNALS & SYSTEMS  Prentice  -Hall Inc.1997

2 张德民.数据通信.北京:科学技术文献出版社， 1997

3 白驹珩.单片计算机及其应用.成都:电子科技大学出版社，1999