数控振荡器（NCO）广泛应用于各种雷达系统和无线收发系统中，其实现方法主要有查表法和坐标旋转算法。查表法会消耗大量的ROM资源，这样不仅增大了能耗，而且增加了芯片的面积；CORDIC算法很好地解决了查表法的问题，而且CORDIC算法由于只采用加法和移位运算，因此很适合在FPGA中实现。

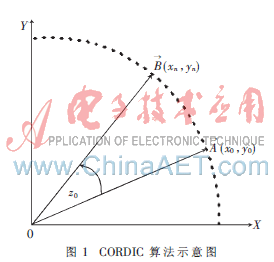
    用图2对上述的旋转过程作解释，旋转开始的初始值是位置①，最终的目标是位置⑤。

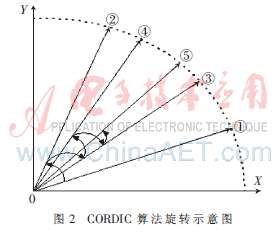
    第一次，位置①与位置⑤之间的夹角z1>0，因此，逆时针旋转一个正切值恰好是2-1的角度，完成了第一次旋转。
    
2 NCO的实现
    CORDIC算法实现的NCO基本结构如图3所示。当有数字中频输入信号时，输出的是数字混频信号，当没有数字中频信号时，输出的是正余弦信号。

    设相位累加器的位宽为n，则NCO的相位分辨率为[1][3]：
  
    确定相位累加器位数后，就可以用Cordic算法设计NCO了。在实现过程中，首先需要建立旋转角度集tan-1(2-i)的查找表，为了保持足够的精度，用下面的表示方法，在硬件里表示直角坐标系的4个区间很容易，在设计中应该注意数字表示法的运用，适当选取二进制和十进制的对应关系，将使整体设计变的更简单。用25 bit表示从0°～360°，二进制l bit代表十进制为：
    360°/225=0.000 010 728 8°。
    正弦、余弦函数旋转变量为[2]：
    当i=0时，arctan(1)=45°= 25'b0_01000000_00000000_
00000000
    当i=1时，arctan(1/2)≈26°=25'b0_00100100_11111010_
01001111
    当i=2时，arctan(1/4)≈14°=25'b0_00010011_11101001_
00111110  
    当i=3时，arctan(1/8)≈7°=25'b0_00001001_11110100_
10011111
    当i=4时，arctan(1/16)≈4°=25'b0_00000101_10110000_
01011011
    当i=5时，arctan(1/32)≈2°=25'b0_00000010_11011000_
00101101
    当i=6时，arctan(1/64)≈1°=25'b0_00000001_01101100_
00010110
    …
    在具体实现时，由于正弦、余弦函数输出值小于1，可定义10 bit二进制数表示输出值-1～+l。为了提高运算速率，采用了8级流水线的方式，QuartusII软件生成的模块如图4所示。各信号的定义见表1。

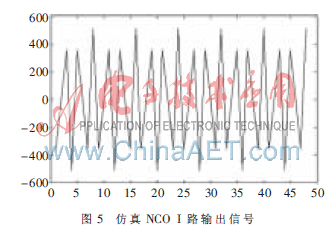
    本设计雷达中频信号为30 MHz，设定采样频率fs=48 MHz，则本振频率fc=18 MHz，采样频率约是本振频率的3倍，如果按采样频率对本振信号进行采样，大约每3个点就循环出现一次，用Matlab仿真的结果如图5所示。

    低成本CycloneIII FPGA是Altera Cyclone系列的第三代产品。Cyclone III FPGA系列前所未有地同时实现了低功耗、低成本和高性能，进一步扩展了FPGA在成本敏感大批量领域中的应用。本设计中选用CycloneIII系列的FPGA芯片。
    CycloneIII EP3C25采用了1.2 V内核，65 nm工艺，由QuartusII 7.2以上版本软件支持，可以重复编程，通过JTAG接口或者EPROM加载程序，内部有PLL、高速I/O接口和乘法器等模块，主要内部资源参见表2。

    封装的不同，EP3C25的引脚数和可用用户IO数也不相同，详见表3。

    本设计选用240引脚的PQFP封装FPGA芯片EF3C25Q240C8N。
    图6所示波形是采用CORDIC算法在硬件上实现NCO，通过QuartusII软件内嵌的逻辑分析仪SignalTapII观测到的I路信号。与图5比较可看出，采用CORDIC算法在硬件上实现NCO获得成功。

    CORDIC算法解决了查表法实现NCO面临的问题，而且具有很高的分辨率。本设计用Altera公司CycloneIII EP3C25 FPGA芯片，在硬件上实现NCO，同时为了提高其运算速率，采用了8级流水线结构，提高了系统的性能。
参考文献
[1] 姜宇柏，游思晴.软件无线电原理[M].北京：机械工业出版社，2007.
[2] Uwe Meyer-Baese著.数字信号处理的FPGA实现[M]. 刘凌，译.北京：清华大学出版社，2006.
[3] 胡广书.数字信号处理[M].北京：清华大学出版社，1997.
[4] CycloneIII Device handbook，Volume 1.