摘 要: 给出了一种基于ti" title="ti">title="TMS320C30" title="TMS320C30">TMS320C30">TMS320C30的磁悬浮轴承不平衡补偿方案。利用锁相环路实时跟踪转速,产生与转速同频的正弦信号,对不平衡位移信号进行自适应滤波,在很大的转速范围内实现了跟踪补偿。该方法简单、易于实现,试验结果表明了其有效性。
关键词: 电磁轴承 锁相倍频器 振动控制 不平衡补偿
旋转机械由于转子的质量不平衡会引起系统强烈的振动。由主动磁悬浮轴承支承的转子系统,由于电磁力与控制电流和位移具有非线性关系,当转速达到一定程度时,不平衡振动的幅值将超过气隙,转子发生碰摩,使系统失控。该失控转速远低于系统的临界转速[1]。因此,磁悬浮轴承系统的不平衡补偿显得尤为重要。
众所周知,陷波器是消除正弦干扰的常用方法,早期的不平衡补偿就是在已知转速的情况下在系统的闭环回路中插入一中心频率为转速的陷波器[2],但却存在稳定性差的问题[3]。Raoul等[4]提出了一种不平衡位移补偿的通用陷波器结构,通过在陷波器中插入T矩阵解决了该问题。本文基于此,给出了一种利用TMS320C30的实现方案,该方法对于刚性转子,可以在很大的转速范围内对不平衡位移进行跟踪补偿。
1 系统方案
文献[5]中给出了不平衡补偿的基本原理、稳定性分析和算法,本文主要介绍相应的硬件实现。如图1所示,试验系统由两部分组成:
(1) 模拟PID控制的5自由度轴承——转子系统;
(2)基于TMS320C30数字信号处理器的不平衡补偿系统。
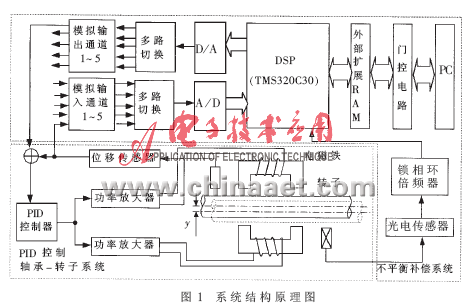
TMS320C30的外围电路主要有多路模拟量I/O通道、A/D、D/A、外部扩展RAM、由PC机总线的数字接口和锁相倍频器构成的同步脉冲发生器。DSP" title="DSP">DSP子系统与PC机间的连接如图2所示。
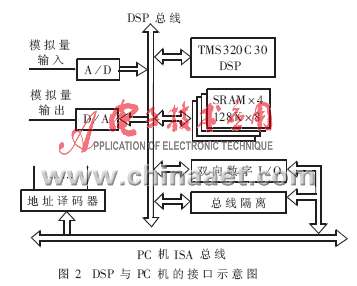
DSP和PC机间通过双向数字接口进行通信,为了便于大数据量的快速传输,扩展RAM同时挂接在DSP总线和PC机的ISA总线上,由总线隔离器隔离,这样扩展RAM将在DSP和PC机中映射到不同的内存页上。一次数据传输的过程如下:当DSP完成相应的数据采集和处理并准备好数据时,就向PC机发出数据传输请求;PC机响应请求并做好传输准备后,向DSP发出应答信号,要求占用总线;DSP响应该请求后挂起系统,然后通知PC机可以占用总线;PC机收到该消息后进行内存换页,从RAM中取走数据,然后再向DSP发出重新启动消息;DSP响应该消息解除挂起,继续运行。
2 补偿算法
陷波器结构如图3所示,补偿算法[5]为:
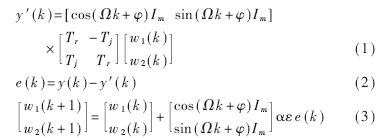
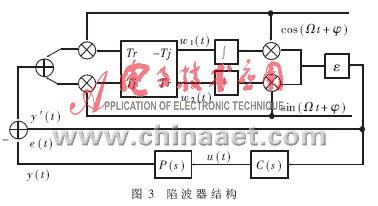
(1)、(2)、(3)式即为补偿的递推算法,y′(t)为输出的补偿信号,α是采样周期,φ是初相位,可取任意值,为计算简单,取φ=0。w的初值可取为:

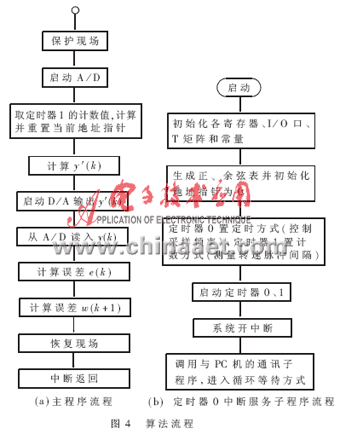
补偿算法用定时器0的中断服务子程序实现。系统启动后,首先进行相应的初始化,然后生产256点的正、余弦函数表并初始化地址指针为0。然后设置定时器0为定时工作方式,时间为采样周期;设置定时器1为计数工作方式,和外部转速脉冲信号同步,并用其计数调整地址指针以确定正、余弦信号的当前值。最后启动定时器并开中断,系统进入与PC机的通信方式,检查并接受PC机发出的各指令,完成相应的操作。
系统主程序的流程如图4(a)、定时器0的中断服务子程序流程如图4(b)所示。
3 参考正、余弦信号发生器
由文献[4~5]可知,该自适应陷波器的关键是产生与不平衡激励同频率的正、余弦参考信号,并且能在一定的范围内自动跟踪转速的变化。为此,利用查表法和DSP的定时器实现一个软信号发生器。
首先,在内存中预先存储两张正弦和余弦表(系统启动时载入),用一个地址指针指向当前值,为了保证一定的精度,取256点。然后,通过光电传感器检测转速,每转产生一个脉冲,经锁相环16倍频后作为DSP的外部中断信号,每中断一次,将地址指针增加16,从而实现了与外部转速信号的同步。
由于DSP系统的采样频率较高(4kHz),当转速较低时,上述方法得到的正、余弦值误差较大(因为实际只使用了16个点的值),因此在用DSP的一个定时器(定时器0)控制采样时间的同时,用另一个定时器(定时器1)测量两次中断的时间间隔,即转速周期的1/16。当定时器0中断时,挂起定时器1,计算定时器1中的计数在T/16中所占的比例,然后据此移动指向正、余弦函数表的地址指针,这样就可以较准确地给出当前的正、余弦值。
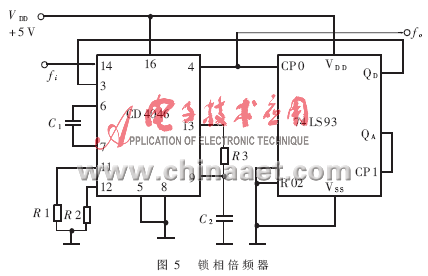
倍频器由集成锁相环和16进制计数器构成,其中心频率在100Hz左右,锁相范围可以设计到10~1000Hz,相应的转速跟踪范围为600~60000转。电路如图5所示。
4 试验过程及结果
以一个模拟PID控制的五自由度电磁轴承-转子系统为对象,对其中的一个径向轴承进行了不平衡补偿,试验转速为6030r/min。
4.1 灵敏度函数测量
利用上述的软正、余弦信号发生器产生的与转速同步的正弦信号,通过一个D/A通道馈入某个自由度的控制回路,同时采集各控制回路的响应,据此就可求得系统的灵敏度函数。测试由DSP和PC机配合完成,DSP完成相应的激励和响应信号数据采集,然后将测量数据传输给PC机,由PC机进行后续的数据处理。
为了提高统计进度,试验中共采集了30组(每组2048点)进行平均,得到该径向轴承两个通道的灵敏度函数为:
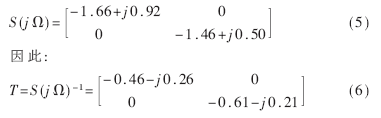
4.2 不平衡补偿试验结果
按照测得的灵敏度函数进行不平衡补偿,试验结果如图6所示。
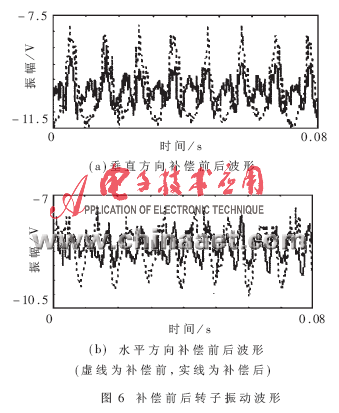
从图中可以看出,在系统保持稳定的前提下,不平衡补偿取得了相当好的效果,转子的同期成分得到了很大的衰减。
本文给出的利用TMS320C30的电磁轴承不平衡补偿方法,对于刚性转子,可以在一个很大的转速范围内对不平衡位移进行跟踪补偿,衰减高速转子同期振动成分;硬件和算法简单,便于实现。
参考文献
1 罗 岷. 电磁轴承-转子系统补平衡补偿技术的研究:[硕士学位论文]. 西安:西安交通大学工程与科学研究院,1999
2 Masujiro H., Tadao K. Adaptive Filtering for Unbalance Vibration Suppression. Proc. 4th Symp. on Mag-
netic Bearings, ETH Zurich, Aug. 1994
3 C.R.Knospe. Stability and Performance of Notch Filter Control for Unbalance Response. Proc. Int. Symp. on
Magnetic Suspension Technology,NASA Langley Research Center, Aug. 1991
4 Raoul H.,Conrad G.,Rene L.Unbalance Compensation Using Generalized Notch Filters in the Multivariable
Feedback of Magnetic Bearings. IEEE Trans.on Control Systems Technology, 1996;4(5):580~586
5 孙岩桦,罗 岷,虞 烈.基于自适应陷波器的电磁轴承不平衡补偿方法. 振动工程学报,2000;13(4):610~615

