引言
    径向基函数(Radial Basis Function，RBF)神经网络具有结构简单，学习速度快等优点，在函数逼近、系统辨识、模式识别等领域得到了广泛应用。
    构造RBF网络的关键是合理选取径向基函数的数量和中心向量。目前，比较常用的方法主要有K均值聚类法、C-Means算法等。这些方法都是在人为确定径向基函数的数量和初始向量之后，采用基于欧氏距离的最近邻方法来实现聚类的。对于类间距离大，类内距离小的样本可以得到比较不错的结果，而对于类间交错较大，类内距离大的情形，这种方法的分类能力将严重减弱，从而不利于网络的泛化应用。另外，网络的训练过程和工作过程完全独立，如果外部环境发生变化，系统的特性会随之发生变化，由此需要重新对网络进行训练，这使问题变得更加复杂，也使网络的应用领域受到限制。
    针对以上算法存在的问题，本文提出了一种RBF网络的自适应学习算法。该算法事先不需要确定RBF的数量和中心向量，而是在学习过程中，根据误差在输入空间的分布，自适应地增加RBF的数量，并适当调节中心向量。为了不使RBF的数量过于膨胀，还制定了相应的删除策略，该策略通过综合评价每个RBF对网络所作的贡献，然后删除贡献小的RBF，使网络结构始终保持简洁。

1 RBF神经网络
    RBF网络是一种三层前馈网络，由输入层、输出层和隐层组成。其中，输入层和输出层皆由线性神经元组成；隐层的激活函数(核函数)采用中心径向对称衰减的非负非线性函数，其作用是对输入信号在局部产生响应。输入层与隐层之间的权值固定为1，只有隐层与输出层之间的权值可调。
    设输入矢量x=(x1，x2，…，xn)T，隐层节点个数为m，RBF网络的输出可表示为：
   
    式中：ωi是第i个隐层节点与输出层之间的权值；φi(‖x—ci‖)，i=1，2，…，m为隐层激活函数。通常采用如下高斯函数：
   
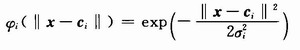
    式中：σi和ci分别表示该隐层节点的宽度和中心矢量；‖·‖是欧氏范数。

2 RBF网络自适应学习算法
    RBF选取得越多，网络的逼近精度越高，但同时也会使网络的泛化能力下降，因此，在满足一定逼近精度的条件下，应选取尽可能少的中心向量，以保证网络有较好的泛化能力。本文提出的算法，根据网络的输出误差在输入空间的非均匀分布，以及每个RBF对网络所作贡献的大小，通过相应的添加和删除策略对网络参数进行自适应调整，使网络的逼近性能和泛化能力都达到较高的要求。同时，网络的训练和工作可以交替进行，所以它能够适应外界环境的缓慢变化。
2．1 添加策略
    添加策略综合考虑了网络输出误差在输入空间的非均匀分布。需要统计每个输入矢量产生的输出误差，然后通过比较找出误差相对较大的点，再在这些点附近适当地插入隐层节点。
    设(xk，yk)，k=1，2，…，N是一组训练样本，初始时刻，隐层节点数为零，每次执行添加操作，依据以下准则判断是否添加隐层节点：
   
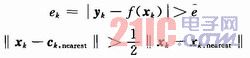
    式中：是网络输出均方误差；ck,nearest和xk,nearest分别对应与输入向量xk最接近的隐层节点中心和输入向量。如果满足添加条件，则将(xk+xk,nearest)／2设为新的隐层节点中心，将ek设为新节点的权值，中心宽度取。
2．2 删除策略
    由于RBF神经网络是一种局部感知场网络，网络总的输出取决于隐层与输出层之间的权值和隐层节点中心与输入矢量之间的距离。进行训练时，所选取的训练样本相对比较稀疏。当某一个隐层节点中心离每一个输入矢量都很远时，即使其权值是一个较大的数，也不会对输出产生太大的影响。在训练结束后进行检验的过程中，检验的数据一般都比较密集，若某些输入矢量离该隐层中心较近，则输出会受到很大的影响，这使网络的泛化能力变差。因此需要制定一种策略来删除这样的隐层节点，由此引入了删除策略。
    删除策略是针对每个隐层节点对整个网络所作贡献的大小不同而提出的。贡献大的节点，继续保留；贡献小的节点，则删除。对任意隐层节点i，用Ai来表示它对整个网络所作的贡献。Ai定义为：
   
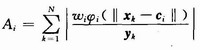
    执行删除操作前，先对Ai进行归一化处理，即。最后的判断规则为：若，则删除第i个隐层节点，其中θ为判决门限。
    在采用梯度下降法调整隐层节点中心位置和权值的过程中，需要计算每个输入矢量对应的输出误差ek，以及每个隐层节点的输出值φ(‖xk-ci‖)。而执行添加和删除操作时也需要计算ek和φ(‖xk-ci‖)。为了减小计算量，提高运算效率，可以在调整隐层的中心位置和权值的过程中先保存ek和φ(‖xk-ci‖)的值。
2．3 算法流程
    自适应RBF神经网络学习算法的具体流程如图1所示。对RBF进行训练之前，先确定最大训练次数M和训练允许误差Er，作为训练结束的条件。

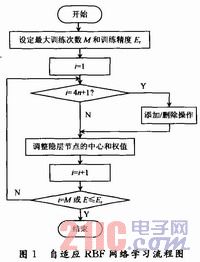
    整个算法的流程大体可分成三个部分。第一个部分是调节隐层节点的中心位置和隐层与输出层之间的权值。本文采用梯度下降法，每循环一次，相应地调节一次。第二个部分是执行添加操作。添加的策略是根据输出误差在输入空间分布的不均匀性而提出的。如果执行该操作过频，不但会减小隐层节点的中心位置和权值的调节速度，而且会造成隐层节点数目过多，计算量增大，导致过度拟合。考虑到以上因素，采用间歇的方式执行添加操作，只有当i=4n+1(n=0，1，2，…)时，才执行添加操作。第三个部分是执行删除操作。如果执行该操作过频，对于一些新增加的隐层节点，其中心位置和权值有可能还没来得及调整就已经被删除了，所以也采用间歇的方式执行。当i=8m+7(m=0，1，2，…)时，才执行删除操作。
2．4 RBF网络参数调整算法
    本文采用梯度下降法调整RBF的隐层节点中心位置和权值。设隐层节点的数目为m，一共有N组训练样本：(x，y)={(x1，y1)，(x2，y2)，…，(xN，yN)}。神经网络的实际输出为：。选取均方差为误差函数，取ρ1和ρ2为学习率。
    (1)调整隐层节点的权值
   
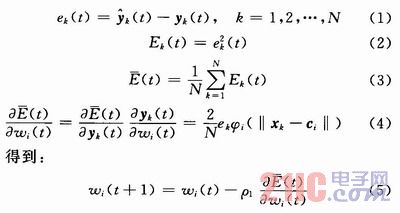
    (2)调整隐层节点中心的位置

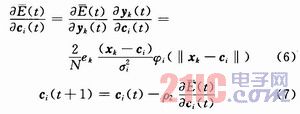
3 仿真实例
    (1)对随机曲面进行恢复
    仿真中定义曲面方程如下：
   
    原始数据集所得曲面图像如图2所示。

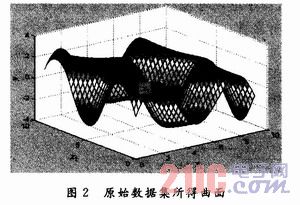
    以x(x=x1，x2)为输入矢量，其中，x1和x2分别以1为间隔在区间[0，9]内均匀取值，一共得到100组输入数据(x1，x2)。选取ε=0．02，θ=0．3，ρ1=0．1，ρ2=0．05。经过20次训练，最后得到的网络具有41个隐层节点，系统的均方误差为0．023 3。拟合后的曲面图像如图3所示。

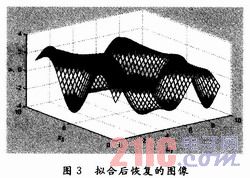
    (2)对θ取不同值时的比较，结果如表1～表3所示。

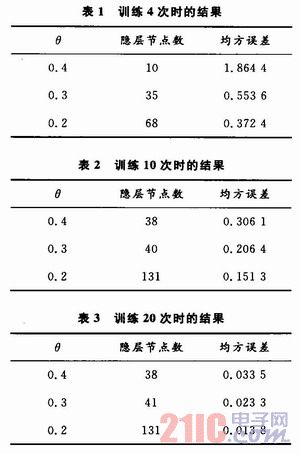
4 结语
    针对RBF神经网络隐层节点的参数和数量难以确定的问题，提出了一种自适应的学习算法。该算法事先不需要确定隐层节点的中心位置和数量，而是通过相应的添加和删除策略实现的。添加策略是根据输出误差在输入空间分布的不均匀而提出的，通过执行相应的操作可以使隐层节点的数目在学习过程中自适应的增加。同时，为了使隐层节点数目不过于膨胀，还制定了删除策略。它先分析每个隐层节点对整个网络所作的贡献，然后删除贡献小的节点，以保持网络结构简单。仿真研究表明，该网络不仅灵活性高，结构简单，精度高，而且具有较好的泛化能力。