麻醉深度监测不仅对于提高麻醉质量和保障手术安全,而且对减少麻醉并发症以及控制麻醉药品用量具有极为重要的意义。因此,麻醉深度监测一直是外科手术关注的重要问题。自Gibbs等人首次提出用脑电信号EEG(Electro Encephalo Gran)监测麻醉深度的可能性,已引起人们对应用EEG监测麻醉深度的研究。近年来利用脑电信号反映镇静水平和麻醉药物浓度,以用于麻醉深度的监测,并越来越受到临床重视,成为研究的热点。早期对脑电信号监测麻醉深度主要是依靠EEG波形的时域特征分析,随着快速傅里叶变换(FFT) 技术的成熟,越来越多的EEG频域特征,如中间频率(MF)和谱边缘频率(SEF)等被用来反映麻醉深度。如今,最为流行的方法是EEG的双谱指数 (BIS)[1],它较灵敏地反映了麻醉深度。但由于存在对不同药物、不同麻醉方法反应不同的缺点,使其不能独立应用于临床麻醉监测。迄今为止尚未寻找到普遍适用的,且适用于临床麻醉深度实时监测的特征指标。由于脑电信号中包含了丰富的、与意识及记忆相关的信息,Theiler等人的研究表明脑电是非线性的[2],但不是源于低维的混沌;Pritchard 等人也指出脑电不是低维的非线性系统[3]。因此脑电信号具有非线性和混沌的特征,而熵(Entropy)则是描述这些特性的重要指标[4-5]。
目前非线性动力学方法被广泛地应用于非平稳信号的处理,时频均谱熵[6] TBSE(Time-Frequency Balanced Spectral Entropy)分析是其中之一。脑电信号是一种非平稳信号,而熵分析方法适合于对脑电信号的处理。时频均谱熵是一种对复杂性进行度量的分析方法,它不需要对时间序列粗粒化,仅需很短的数据即可达到稳定的值。与其他复杂性参数相比,具有计算速度快、适合在线实时分析的特点,因此在信号处理相关领域得到很好的应用。EEG序列的时频均谱熵表现了EEG序列中产生新模式的概率大小,其概率越大,序列的复杂性越大,时频均谱熵值也越大。
1 时频均衡谱熵方法
时频均衡谱熵(TBSE)是在shannon熵[7]的基础上阐述频谱熵的概念,它结合时域和频域分析,应用窗可变的短时傅里叶变换,计算特定脑电信号频谱带的不规则性。TBSE算法中计算了两个熵值:(1)状态熵(SE)。反映了脑电主要频带(0.8 Hz~32 Hz)的作用;(2)反应熵(RE)。反映了脑电和额肌(0.8 Hz~47 Hz)的快肌肉活动的共同作用。二者差值(RE-SE)即为肌电熵(EMG)。状态熵和反应熵可以区分有意识和无意识状态,可通过肌电活动反映镇静程度和疼痛反应,体现了麻醉深度监测中应用多种方法进行综合分析的趋势(如脑电结合肌电熵分析)。
(1)首先在不同的频率段计算出能量谱,然后对所有的能量谱元素求和再进行归一化:

TBSE作为一种可描述系统复杂性的参数,它具有一些相对其他复杂性参数所不具备的特征:
(1)通过较短的数据序列,即可得到稳定的肌电熵值。
(2)原始信号不需要粗粒化。
(3)具有很强的抗噪声及抗干扰能力,尤其是对随机产生的瞬态强干扰具有良好的屏蔽作用。因为随机产生的较强干扰势必造成距离大于给定的相似容限距离,而在距离检测时被忽略。
(4)适用于确定信号、随机信号以及确定信号和随机信号组成的混合信号。
因为生理信号通常是由确定信号、随机信号组成的混合信号,而且分析所需数据长度较短,很适合非平稳信号(如脑电)的监测,因此TBSE非常适合于临床生理信号的监测分析。
2 脑电信号数据采集与处理
2.1 数据采集
在麻醉深度监控中,感兴趣的EEG信号频率范围一般<70 Hz,通常选择系统采样频率在200 Hz以上可调,默认为250 Hz。因为要求得到3~4通道的脑电及肌电信号,故信号采样频率采用1 kHz。脑电信号的前端处理主要包括信号采集、放大、A/D转换及去噪。
(1)电极选取:麻醉监测的电极采用BIS公司的电极,这种电极具有与头部接触性好、对人体无损害、无痛、方便等特点。
(2)电极采集位置: EEG的采集位置如图1所示,采集右前额或左前额的脑电信号,并以前额的正中间电极作为参考电极。
(3)滤波、放大及A/D的参数:正常滤波范围是3 Hz~70 Hz,丧失滤波时滤波范围0.25 Hz~100 Hz。采样频率:1 000次/s。通道数:4个电极,2导EEG数据。
2.2 信号预处理
由于头皮记录的脑电信号中通常包含许多干扰(如心电、眼动、肌动等生理学噪声,以及电极或环境噪声等非生理学噪声),这些伪差往往与正常病理特征EEG 的波形或频谱相混淆,容易掩盖EEG的波形特征。因此,获取EEG信号中反映大脑活动和状态的有用信息,就必须有效地去除脑电数据中的伪差。伪差的去除通过对采集到的EEG信号,首先丢弃一些噪声非常大的信号点或者段,然后将信号重组分段。对于每段信号,先检测各种可能的伪差信号的存在性,若检测到某种伪差存在,再进行相应的去除操作,这样可减小计算量。
另外需要注意的是,通常一些干扰,如眼动、肌动,仅在病人清醒状态下存在,在麻醉时则很少受其影响。因此病人在清醒和麻醉期间,应采取不同的去噪算法,当病人状态发生变化时,应及时切换去噪算法,通过肌电熵阈值判断病人状态转换时刻,进行去噪算法选择。脑电信号预处理部分框图如图2所示。
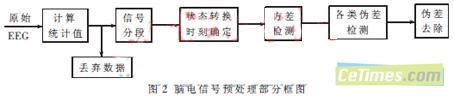
在采集到原始脑电信号中,不可避免会出现超过放大器动态范围的信号点或段,这是由于放大器设置不合适,或者电极在头皮上发生移动造成的。这类伪差由于无法重建,所以被干扰的部分信号必须丢弃。根据采集到的信号的均值统计特性,确定其阈值并进行识别,然后判断是否丢弃信号。
2.3 伪差检测和去除方法
预处理过程中,将前几段EEG信号的方差与前几段的平均值相比,若存在明显差异,则标记为含噪段,然后进行后续的各种伪差检测和去除步骤;无明显不同,则标记为无噪段,无需经过后续步骤,直接可以进行麻醉深度参数提取。注意逐段计算过程中前几段的方差均值需要不断更新调整。
(1) 在麻醉监控过程中,病人呼吸是不可避免的,呼吸作用可以通过在EEG上附加一个有节奏的信号(一般0 Hz~0.8 Hz)。对于皮肤的反映,如流汗可能改变电极的阻抗,这些都会产生一些低频波,为EEG带来基线漂移。可采用截止频率为0.5 Hz的高通滤波器滤去这部分干扰。另外,基于感兴趣的EEG信号频率范围有限,故一般将其信号通过一个低通滤波器,其截止频率可选,默认值为70 Hz。
(2)由于EEG是低功率信号,易受环境噪声影响。手术室中,脑电信号获取设备周围可能有大电流设备,它们会引起EEG的工频干扰,在EEG的50/60 Hz和100/120 Hz附近产生大的扰动,与频率有关。因此,在检测时采用计算50/60±2 Hz上的功率占整段信号总功率之比进行干扰判断,若大于某给定阈值,则存在干扰。去除这种干扰,可使用50/60 Hz陷波滤波器,如6th Butterworth滤波器。
(3)眼电信号(EOG)伪差一般是低频(0~16 Hz)高幅波,具有明显的时域模式,一般是方形波或者大的尖峰,可以在时域、频域计算信号特征来识别(根据相邻多个数据段的特征)。应用小波自适应阈值化方法去除EOG伪差,是在EOG存在子带上,选择合适的阈值及阈值化方法去除,既不需要EOG参考通道,也不需要人的干预,可自动去除。
(4)肌电信号(ECG)一般具有周期性,频率主要在13 Hz~32 Hz左右。其检测可利用其自身规律性结合频域特征,提取13 Hz~32 Hz频带信号计算其能量,再根据系数的局部变化选择合适阈值,进行阈值化以突出伪差存在位置,检测伪差发生中心点;利用基于中心点的时序锁定(time- locked)平均计算ECG平均模板除去ECG伪差。肌电熵(EMG)通常持续时间较短,检测其存在性,可应用卡尔曼自适应滤波方法去除,同时也可除去其他瞬态大幅度信号干扰。此外,信号中也可能含有高斯白噪声,可以采用小波Bayes估计方法去除。
3 结果与分析
图3(a)所示为一段清醒期的脑电信号,包含有肌电和眼动的噪声。图3(b)是采用上述方法去噪后的结果,其中眨眼和眼球动干扰明显被去除,高频的肌电干扰也被滤除掉了。表明该滤波器工作可靠有效。
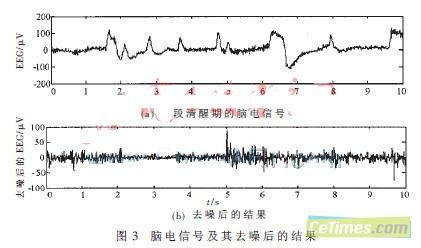
图4(a)、(b)是一段EEG信号及其对应的麻醉药物七氟醚浓度。从图4(c)可以看出病人在注射麻醉药品之后的不同时间段内,EEG的反应熵都有一定的变化。在EEG信号的初始阶段,病人EEG的反应熵较高,其值在0.75~0.85 之间。在麻醉120 s后,反应熵明显下降,麻醉190 s后,反应熵的值在0.4上下波动。EEG信号的肌电熵如图4(d)所示,可以看出,其值在0.1~0.4之间波动,麻醉190 s之后接近于0,表示病人进入麻醉状态。
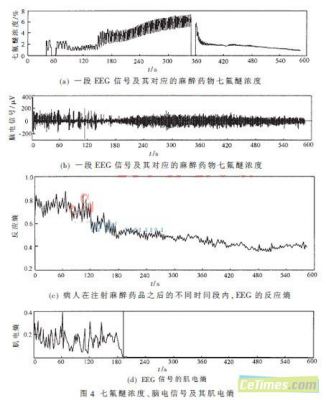
由于病人对外界刺激的反应,在病人清醒或麻醉不足时,额前测得的脑电信号中会出现含有肌电信号(图4(d))。因此肌电信号可作为由清醒到麻醉、由麻醉到觉醒的指示标志信息。根据这一特点,设定一阈值,当肌电熵大于阈值时,病人处于清醒状态;当肌电熵小于阈值时,病人处于麻醉状态。由此判断出状态切换时刻之后,可以对应不同的状态,采取不同的预处理方法:眼电信号和肌电信号的伪差只可能在清醒状态影响脑电信号,因此只能在清醒期进行检测和去除即可;其他伪差检测和去除在整个记录中均可进行。
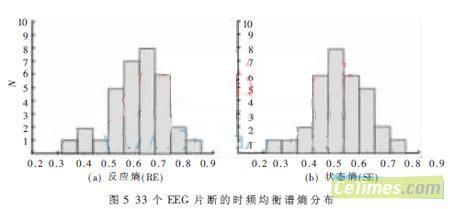
本文从40余例注射麻醉药品后的EEG信号中,选取33个EEG信号片断,进行时频均衡谱熵分析,将分析结果作直方图统计进行分析。图5(a)为注射麻醉药品之后的反应熵分布直方图,可以看出此时EEG信号的反应熵主要分布在0.55~0.80之间。图5(b)为注射麻醉药品之后的状态熵分布直方图,可以看出此时EEG信号的状态熵主要分布在0.45~0.75之间。可见,随着麻醉深度的不同,反应熵的值会随之变化,麻醉深度越深,反应熵的值越小;麻醉深度越浅,反应熵的值越大。这是由于麻醉深度的加深,大脑神经元的兴奋性受到抑制,EEG信号的随机程度降低,产生新模式的概率降低,反应熵的值也就相应降低。麻醉深度减轻时则刚好相反,这一结果很好地验证了时频均衡谱熵作为临床麻醉深度监测指标的正确性和可行性。
从麻醉状态下EEG信号的时均衡谱熵分析结果可以看出,在注射麻醉药品180 s左右,反应熵的值开始下降,190 s肌电熵趋于0,病人进入麻醉状态,这一结果很好地印证了七氟醚的药理特性。通过分析可以看出,EEG序列的时均衡谱熵与麻醉深度之间有着密切的关系,可灵敏地反映出麻醉深度的变化。虽然在表征麻醉深度的变化趋势有些缓慢,但由于时均衡谱熵本身具有达到稳定值所需计算窗口小、抗干扰性强的特点,作为麻醉深度的实时监测,仍然是一种好的方法。实验结论是基于七氟醚麻醉药得到的,与其他麻醉药的相关性结论还待进一步的深入研究。
参考文献
[1] BRUHN J, BOUILLON T W, RADULESCU L,et al. Correlation of approximate entropy, bispectral index, andspectral edge frequency 95(SEF95) with clinical signs of anesthetic depth during coadministration of propofol and remifentanil[J]. Anesthesiology, 2003,98:621-627.
[2] THEILER J, EUBANK S, LONGTIN A, et al. Testing for nonlinearity in time series: the method of surrogate data [J]. Physica D, 1992,58(1):77294.
[3] PRITCHARD W S. Dimensional analysis of resting human EEG: Surrogate data testing indicates nonlinearity but not low-dimensional chaos[J]. Psychophysiology, 1995,32(3).
[4] BEIN B. Best Practice & Research Clinical Anaesthesiology[J]. Entropy,2006, 20(1):101-109.
[5] BRUHN J, ROPCKE H, REHBERG B, et a1. Electroen cephalogram approximate entropy correctly classifies the occurrence of burst suppressionpattern as increasing anesthetic drug effect[J]. Anesthesiology,2000;93(4):981-5.
[6] VIERTIO-OJA H, MAJA V, SARKELA M, et a1. Description of the Entropy algorithm as applied in the Datex-Ohmeda S/5entropy module[J]. Acta Anaesthesiol Scand, 2004,48(2):154-161.
[8] BRUHN J, LEHMANN L E, ROPCKE H, et al.Shannon entropy applied to the measurement of the electroencephal-ographic effects of desflurane[J].Anesthesiology, 2001, 95:30.

