摘 要: 简略介绍了PageRank算法,给出其在孤立点检测应用中的算法及实验结果和分析,最后将该算法与其他算法进行比较。结果证明,该方法能较准确地检测到孤立点,并能适应各种图形。
关键词: PageRank; 算法; 孤立点检测
在数据挖掘和图像分析中,孤立点的检测是一个重要的内容。在很多情况下,发现孤立点比发现普通情况更有意义,如:KNORR E M和NG R T把孤立点检测方法应用到运动员数据NHL(National Hockey League)的分析中,从而找到那些特别的运动员;YAMANISHI K和TAKEUCHI J将检测方法应用到股票的变动检测中等等。另一方面,PageRank(页面分级)算法是PAGE L和BRIN S在就读斯坦福大学研究生院时研发出来的,他们后来创建了著名的Google公司,现在分别担任该公司的CEO和总经理。而PageRank算法就是Google搜索服务的一个核心技术。事实证明该算法在搜索服务上是非常成功的。
页面分级的思想与在二维平面上作孤立点检测的思想非常相近,于是本文把PageRank算法运用到孤立点检测中,并给出实验结果和本文算法与其他的主流算法的比较。
1 PageRank算法
1.1 PageRank算法的核心思想
对于世界上众多的网页,这些网页有的十分重要,而有的重要性十分轻微。当想要快速地在这么多的网页中找到想要的网页时,无论想查关于哪一方面的信息,都会希望别人给出的查找结果是那些重要的网页,而不是微乎其微的网页。所以在查找之前就应该把网页(或者称为页面)进行重要性排序。用什么来衡量一个页面的重要性呢?计算机能否由页面的内容来判断页面的重要性呢?答案是不能,计算机还没先进到这个程度。但PageRank算法给出了一个行之有效的思想:从许多优质的页面链接过来的页面,必定还是优质的页面[5]。这一思想容易理解,如果有很多的页面链接到A页面,那么就认为A页面是比较重要的,那如果B页面被A页面链接(反过来说也就是A页面链出到B页面),因为A页面被一个认为重要的页面链接,所以也就把B页面的重要性作一个大幅度的提高,认为B页面也是重要的。通过互联网中页面间本身就存在的链接,是容易算得页面的重要性的。
但另一方面,有些页面为了提高重要性,相互间做一种商业上的链接,为了杜绝这一种情况,PageRank在计算页面重要性的时候,对于链接进来的页面也是要考虑其重要性的,即重要性高的页面链接进来,则对当前页面重要性的提高有很大帮助;重要性低的页面链接进来,则对当前页面重要性的提高帮助很小。
1.2 PageRank算法的简略步骤
假设有N个页面,这些页面间有相互链接。
(1) 制作一个N×N的矩阵S,如果页面a链出到页面b,则S(a,b)=1;
(2) 将矩阵S转置,得到矩阵S′,因为这里关心的不是该页面链出到多少其他的页面,而是有多少其他的页面链进来当前页面;
(3) 对S′的每一列,算出非零元的总数sum,在把该列中的每一个非零元除以sum。这样就得到一个新的矩阵M;
(4) 算出M的特征值和特征向量;
(5) 找出最大特征值所对应的特征向量,并把该特征向量标准化。标准化后的结果就是各个页面对应的重要性的度量值,称为PageRank值。
2 PageRank算法在孤立点检测中的应用
2.1 应用思想
把各个不同的页面看成是二维平面上的点,按孤立点检测的定义,也就找出了那些离群的点,即这个点周围的其他点很稀疏。
有必要把点按密度值进行排列,在这里,点的密度值就对应于页面的PageRank值,即重要性。当一个点所处位置的一定范围内出现的其他点越多,则这个点的密度值就越大,反之则越小。
是否基于密度的聚类分析就可以解决这个问题了呢?可是基于密度聚类分析算法最终得出的结果是受人为因素干扰比较大,当所选的半径不同时,得出的结果有很大的差别。本文使用PageRank算法判断一个点周围其他点的数目时,选取的半径可以为任意值(当然,不能离谱)。
以点a为中心、r为半径画圆,当出现在这个圆中其他点的数目达到一定量时,就说明点a与出现在这个圆的其他点是有链接的,即对应于页面a链接到其他的页面。接下来的操作就与页面分级算法基本一样了。
2.2 应用步骤
(1) 算出二维平面上任意两点间的距离;
(2) 建造一个N×N的矩阵S,选择半径r,当a、b两点间的距离小于r时,S(a,b)=1;
(3) 将矩阵S转置,得到矩阵S′;
(4) 对S′ 的每一列算出非零元的总数sum,再把该列中的每一个非零元除以sum,这样就得到一个新的矩阵M;
(5) 算出M的特征值和特征向量;
(6) 找出最大特征值所对应的特征向量,并把该特征向量标准化。标准化后的结果就是各个页面对应的重要性的度量值,称为PageRank值;
(7) 把PageRank值排列,再利用稳健的孤立点检测方法把孤立点检测出来。
3 实验以及分析
该实验是在Matlab环境下实现的。点群如图1所示。
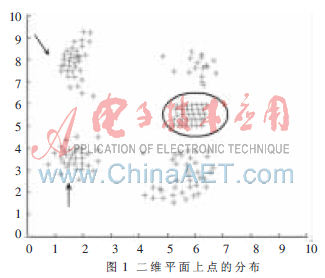
从图1可以看到,共有156个点,点的分布类型有逼近高斯分布(左边用箭头指的两个),有均匀分布(右边圈起来的)和其他的不规则矢量分布(右边剩下的上下两个)。把PageRank值算出来,并标在xoy面上,如图2所示。

从图2中挑出3个特征向量很小的地方,如箭头所标,这里虽然标了3个箭头,但有5个点,第一个箭头处有3个点。这5个点的序号分别是95、96、97、140和156,而这幅点群的序号和坐标如表1所示。
这5个点的位置如图3所示。

可以看到这5个点明显都是孤立点,其他的孤立点也可以由同样的方法找出,这里就不一一找出来了。值得注意的是,这幅点群中的分布情况是多种的,但PageRank算法都能很好地把孤立点找出来。
4 实验结果比较
与其他的孤立点检测算法相比较,PageRank算法有如下优点:
(1)与基于密度的检测方法相比较,它不受给定的半径影响。
因为在该算法中,半径的确定只是为了判断该点与其他点是否有“链接”而已,就像判断各个页面之间是否有链接,而处于稀疏群的点与处于密集群的点,无论半径画得大小,只要画得不要太离谱,那处于密集群里的点与其他点的链接数肯定要比处于稀疏群里的点与其他点的链接数多,而最后是根据链接数的比重来排序的,也就是说半径的大小不影响排序的位置,当然对检测也就没什么影响了。
(2) 考虑如图4所示的这幅图,当用同样的半径去画圆时,圆1里的点只有3个,圆2中的点有4个,但能说左边箭头所指的点是孤立点而右边箭头所指的点不是孤立点吗?

显然,从整幅图来看,左边的是一个群体,而右边的4个点才是孤立点,或者说是一小群孤立点。其原因就在于与左边的点1邻近的点都是密集度高的点,即它背后有一整个群体做支持,而与右边的点2邻近的点都不是密集度高的点。
这样就把邻近点的密集度也考虑进来了,这就像“从许多优质的页面链接过来的页面,必定还是优质的页面。”这句话所说的那样,而在这里就是“与许多密集度高的点邻近的点,必定也是密集度高的点”。
(3) 由特征向量的图(如图2所示)可以看出,有许多的“波谷”,这些点都是特征向量值小的点,当然,“波谷”凹的程度也有大小,这样,就能通过选择一个尺度来找不同的孤立点,当选一个大尺度的时候,孤立点就少一些,反之,孤立点则多一些。
本文首先简略介绍了PageRank算法的思想,其在Google上的成功应用证明这种算法是高效的;再由网页与二维平面上的点的相似性到把该算法应用在孤立点检测上,当然在具体算法上,要稍加改变,例如用什么方法来确定两点间是否有“链接”等。文中还给出了一个实验结果和分析,图中共有156个点,当然这在实际应用中是不够的,这里不过只是为了说明PageRank算法能在孤立点检测上运用而已。
参考文献
[1] 蔡利栋,傅瑜. 稳健的孤立点检测——从中位数求方差[J].计算机科学,2006,33(8)(增刊):185.
[2] 范结. 数据挖掘中孤立点检测算法的研究[D]. 长沙:中南大学计算机应用技术,2009.
[3] 陆声链,林士敏.基于聚类的孤立点检测及其应用[D]. 桂林:广西师范大学数学与计算机科学学院, 2003.
[4] Hajime BABA.Ph.D.Google的秘密——PageRank的彻底解说(2004-02-24)[2010-03-20].http://www.kreny.com/pager-ank_cn.htm.
[5] PAGE L, SERGEY B, RAJEEV M, et al. The PageRank citation ranking bringing order to the Web[D].Technical Report. Stanford:Univ. of Stanford InfoLab.1998.
[6] HAVELIWALA T H. Efficent computation of PageRank technical report. Technical Report[D]. Univ. of Stanford Info-Lab,1999.

