摘  要： 文本聚类在很多领域都有广泛应用，而聚类算法作为文本聚类的核心直接决定了聚类的效果和效率。结合基于划分的聚类算法和基于密度的聚类算法的优点，提出了基于密度的聚类算法DBCKNN。算法利用了k近邻和离群度等概念，能够迅速确定数据集中每类的中心及其类半径，在保证聚类效果的基础上提高了聚类效率。
关键词： 文本聚类；基于密度；k近邻；离群度

    文本聚类是指将n篇文章聚集成k类，使得每类内的样本相似度较大，每类间的样本相似度较小。文本聚类是一种特殊的数据聚类，有着自身的特点。文本的聚类对象维数较高，决定了聚类算法需要快速收敛，注重效率。国内外也围绕着文本聚类提出了很多理论和算法，采用的核心聚类算法一般分为两类，一类是基于划分的聚类算法，如K-means算法、CLARANS算法等；另一类是基于密度的聚类算法，如KNNCLUST算法、DBSCAN算法等。
1 基于密度聚类算法的研究与改进
1.1现有算法的缺陷
    K-means算法与DBSCAN算法分别作为基于划分和基于密度的聚类算法的代表，被广泛应用于文本聚类中。其中K-means算法有实现简单、时间复杂度低等优点，但算法需要指定种类数，且对初始点依赖性过强，导致聚类效果不理想；DBSCAN算法则有抗噪音性强、聚类准确性高等优点，但算法的主要阈值参数很难确定，且时间复杂度过高，导致聚类效果不理想。
    本文将K-means算法的特性，融入到利用k近邻概念的基于密度的聚类算法中，提出了DBCKNN算法(Density-Based Clustering using K-Nearest Neighbor)，在保证算法准确性的前提下，提高了算法效率。


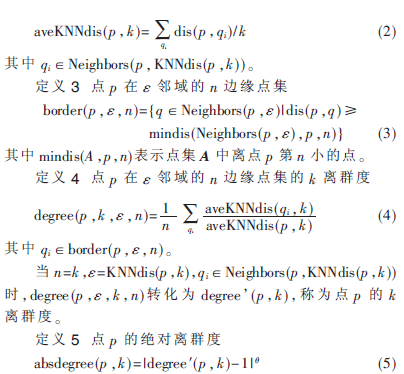
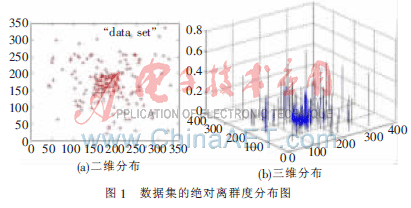
点的绝对离群度域值为(0，+∞)，且值越小，表示点越有可能为类中点，反之，表示点越有可能为噪音点。θ一般取不大于3的正整数，θ越大，不同对象的绝对离群度分布越离散。如图1(a)中类近似为高斯分布，图1(b)中z轴为点的绝对离群度值，其θ取1。可以看出，越是类中心的点，其绝对离群度越小，而类边缘和噪音点都有相对高的绝对离群度值。

    定义6 边缘点集的k平均近邻距离的均值

1.3 算法改进
1.3.1 确定类初始中心核心子算法FINDCENTER(ε)
    现有的基于密度的聚类算法中，通常会对全体点进行一次密度值扫描，导致算法复杂性和空间复杂性过高。改进后的算法，利用划分算法中迭代并更新中心点的思想，可以对定半径的超球体的移动具有指导性，使得落入超球体内部的点相对更多，即超球体的密度相对更大。
    算法1 FINDCENTER(ε)
    算法输入：p，ε；算法输出：p
    (1)以ε为邻域半径，求|Neighbors(p，ε)|和absdegree(p，k)。
   
    算法中的λ取值一般为0~1。λ取值越小，半径变化越小，迭代次数越多，但最终得到类半径的值越准确。算法中的(α，β)域越宽，聚类粒度越大。算法中的n是不大于k的正整数，一般取值和k相同。n取值越大，则时间复杂度越高，但最终得到类半径的值越准确。
1.3.3 DBSCAN算法思想
    在数据对象集中找到absdegree(p，k)大于阈值的对象p后，通过反复迭代FINDCENTER(ε)和ADJUSTRADIUS(p，ε)，找出初始类Ci，并将Ci排除出数据对象集。重复上述过程，生成初始类集。通过初始类集中各类间的包含关系和评价函数，将噪音点集从初始类集中提取出。最后将噪音点集中的对象按与类集中各类中心点的距离分配给各个类。
2 实验
    通过实验对DBCKNN算法的聚类效果和时间效率进行对比和分析。数据集采用两个著名的数据集Iris和KDDCUP1000。测试数据集信息如表1。这两个数据集每一类的数据映射到高维空间中近似为正凸型的超球体，符合文本聚类中所提取的文本特征向量的分布情况，其中Iris为3类，KDDCUP1000为5类。实验用VC6.0编写，在配置PentiumⅣ 2.4 GB CPU、内存1 GB、80 GB硬盘的计算机上运行。

    本文对聚类效果的评判标准采用参考文献[4]中提出的聚类质量判定式：S-Dbw(c)=Scat(c)+Dens-bw(c)，其中c为类集，Dens-bw(c)评价的是各类间的平均密度，值越小表示类间区分度越好；Scat(c)评价的是类内元素的相似性，值越小表示类越内聚。
    对经典算法K-means、DBSCAN和本文提出的DBCKNN算法在聚类效果和效率上做对比。其中K-means算法的k分别取3和5，并对初始点集做预处理，尽量使初始点集分散且局部密度相对大，DBSCAN算法的minpts、eps取2.5，DBCKNN算法的λ取0.5，k、n取20，θ取2，(α，β)取(0.9，1.1)。
    图2为预处理后的K-means算法、DBSCAN算法和DBCKNN算法对测试数据集的聚类效果比较。
    从图2可以看出，虽然已经对初始点集做了预处理，而且对k取了正确的值，但是K-means算法效果仍然不理想。由于DBSCAN算法在数据对象密度的处理上更精确，在数据对象维数较低时，效果略好于DBCKNN算法；而当数据对象维数较高时，高维空间中数据分布稀疏，DBSCAN算法会误将部分数据对象视为噪音点，从而对聚类效果产生负面影响，而由于DBCKNN算法采用k近邻距离作为密度探测半径，对噪音点的处理更加合理，所以在数据对象维数较高时效果要略好于DBSCAN算法。

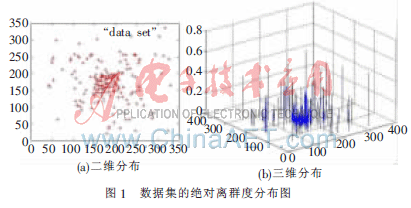
    图3为K-means算法、DBSCAN算法和DBCKNN算法对测试数据集的聚类效率。

    从图3可以看出，K-means算法的效率非常高，在常数次迭代就得到聚类结果，数据规模对聚类效率的影响有限；DBSCAN算法要对所有数据对象的密度进行一次以上的处理，聚类效率依赖于数据规模，导致效率相对低下；本文的DBCKNN算法会根据数据对象局部区域的密度信息来评价这个局部区域所有数据对象的密度信息，所以聚类效率比K-means算法低，但远高于DBSCAN算法。
    本文结合了基于划分的聚类算法和基于密度的聚类算法各自的优点，提出了一种能够快速找到类中心并自适应类半径的聚类算法DBCKNN算法。DBCKNN算法能在对高维空间下每类形似正凸形超球体的数据对象集进行相对准确的聚类情况下，提高算法效率。另外，本文通过分析及实验数据对比，从聚类效果和聚类效率两方面验证了这种改进方法的正确性和高效性。进一步将这种方法和基于语义的聚类方法相结合，应用于聚类搜索引擎等数据挖掘领域，是下一步研究的重点。
参考文献
[1] 孙吉贵．聚类算法研究[J]．软件学报，2008，19(1)：48-61．
[2] KANUNGO T， MOUNT D M， NETANYAHU N， et al． A local search approximation algorithm for K-means clustering[J]．Computational Geometry， 2004(28)： 89-112．
[3] 汪中．一种优化初始中心点的K-means算法[J]．模式识别与人工智能，2009，22(2)：300-304．
[4] HALKIDI M， VAZIRGIANNIS M． Clustering validity assessment： finding the optimal partitioning of a data set[C]． In： Proc．of the 1st IEEE Int’I Conf．on Data Mining．187-194．
[5] 谈恒贵．数据挖掘中的聚类算法[J]．微型机与应用，2005(1)．