引 言
循环冗余校验(Cyclic Re&mdancy Check,CRC)是最为常用的计算机和仪表数据通信的校验方法。CRC码是一种线性分组码,编码简单但具有很强的检错纠错能力。除了各种嵌入式仪表、变频器等设备,还有一些数字型传感器的输出数据也提供CRC码,如数字温度传感器DSl8820、集成温湿度采集芯片SHTll等。但是,各厂商所提供的CRC校验多项式(用于同通信码模除)互有差别,且有CRC一8和CRC一16之分。另外,规定模除余数初始值所有的位有全清0或全置1之分(其CRC硬件生成电路不同),故其模除求余的运算过程也不相同。初接触者往往难以领晤,省略CRC校验使通信的可靠性降低。而不少C语言程序,运算时需要使用较多的RAM单元,较难在80C51、PIC16等低档单片机上运行。
因此,对于嵌入式系统中的CRC校验,事先根据特定的校验多项式,算出1字节数据范围所对应的256个余数,将其作为表格,编程写到程序存储器中查询而避免在线运算,已是非常通用的做法。鉴于此,有些厂商在说明书中就直接给出了这个列表。但如果是CRC一16校验,存储表格要占512字节(CRC一32则需要1 KB),对于有限的单片机ROM资源来说所占比例不小,往往只因为多装了此表,就不得不升级单片机的型号。
本文分析和解释了实际CRC校验码的生成特点,据此给出节省RAM和ROM且运算快速的通用CRC校验编程思想和程序结构,并探讨了用少量硬件实现快速、可靠CRC校验的方法。
1 CRC原理和实际校验码的反序生成特点
一个k位二进制数据在传送时,按一定规律附加一些冗余位而增大其码距,就能检错和纠错。标准CRC码是将原数据左移r位,再用r+1位的特别约定多项式(poly—nomial funetion)模除之,获得最多为r(8、16、32)位的余数,跟随原数据之后生成k+r位的编码发送。接收方再用相同的约定多项式,模除收到的数据,余数为O则传输无误,为其他值则对应各个位的出错。
但是对于实际应用,为加快通信速度,r位的余数并不是每次都传输,而是采用累计模加(异或)的方法,不断地与下一个k位数据异或运算,组成新的中间余数(仍为r位,因一般选择r≥k),再被约定多项式模除得到新的余数值,依此类推,直到所有通信数据都同中间余数异或,再模除完为止。如此得到最终的r位余数,作为全组数据校验的CRC码附在该组数据之后发送。接收方以同样的过程,算得收到数组的最终余数,再同最后收到的CRC码对比(或将CRC码也作为数据,看最后余数是否为O)。当然这样只能查出该组数据的传输是否有错,而不能纠错。
首数据的余数是唯一的,再异或进后续的任何一个特定数据之后,结果依然唯一。所以只要选择r有足够的位数,就能保证多个数据中一旦有个别位传输错误,其最终的CRC余数与传输正确的余数相等的可能性极低,因此能查出传输错误。
对于元器件和不少的设备来说,其最终余数,即组校验的CRC码,是靠硬件快速生成的。为了使硬件电路简化,也为了接收方易于校验编程,往往采用变形生成的CRC码和与其对应的校验处理方式。
对于模除余数的初始值,ISO/IEC 13239标准规定各位(8、16、32)均置1,而DSl8820器件和一些控制仪表的通信CRC码却是清0。在软件编程时要根据不同器件赋予不同的初始值。
特别约定多项式g(x)都是r+1位的,如ISO/IEC13239标准的CRC一8,g(x)=x8+x2+x+1。其最高位恒为1,将其隐含则可简化模除运算,但这样一来后面多位是O,较难在多字节(如16位需2字节)CRC校验中定位计算和存储。因此,大多数CRC码生成和校验的处理都采用将约定多项式反序的方法,即将最低位1放到最高位并丢弃最高次幂系数1,从而将运算和存储都降为r位。
对于CRC一8,g(x)=x8+x2+x+1,去高位反序后的模除数为11100000(OEOH),r=8。
对于CRC一16,g(x)=x16+x15+x2+1,去高位反序后的模除数为OA001H,r=16。
对于CRC一CCITT,g(x)=x16+x12+x5+1,同样处理后的模除数为8408H,但也常用正序值1021H。
对于CRC一32,g(x)=x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x+1,处理后的模除数为0EDB88320H,r=32。
如上处理后,按理说被模除数和余数也应该反序。但这样的话r位的余数在同下一个k位数据模加时不但k位数据应反序,而且必须左端(最高位)对齐进行异或,处理起来不但麻烦也容易出错。因此,实际CRC码的生成和校验一般仍是将余数,即被(模)除数,按正序排列,新数据也仍是右对齐异或进余数中。但是将被模除数原先的左移r位右添0改成了右移r位左添(r个)O。这相当于k+r位被模除数中仅r位被反序(放左端),而前面k位(现放于右端)依然正序。可以看出,按反序原则,实际上每一次都是异或进通信数据的反序值,如11001000B(0C8H)变为000100ll(13H),再异或进被模除数来求取CRC校验码。但由于所有二进制数的反序值都是唯一对应的,所以并不影响生成CRC码的唯一确定性,只是接收方需要按照同样的反序规则处理.
2 嵌入式系统CRC校验的编程
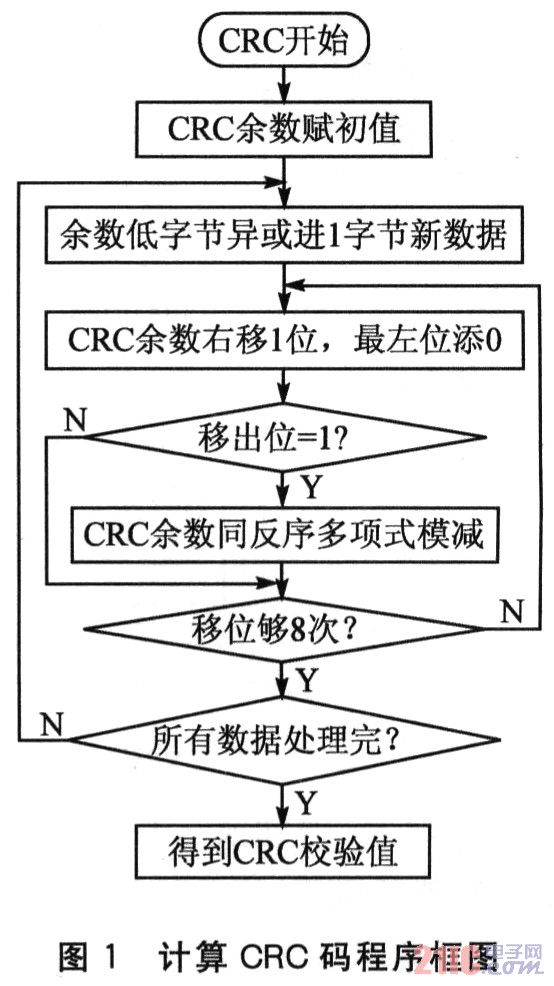
如上所述,k+r位的被模除数采用右移的方法不断地同反序的约定多项式对位模除,也就遵从了从高位向低位不断减余的除法规则。但由于不必求模除的商,因此只要将被模除数不断地右移位,与去掉最高位的反序约定多项式模减,求得余数即可。
但如果被模除数最低位右端的移出位是O,则无论从左端添进多少个O,也不够模除约定多项式(其隐含的最高位是1)。在此情况下该位的商是O,余数不变,不应再同约定多项式对位模减,而要继续左添O右移位,直到当前余数(被模除数)右移出的位值为1才够模除(商1),才可将余数再对位模减一次多项式。由此看出,将约定多项式去掉最高位,可以使模减(异或)的计算位数r减少(一般r都正好是1字节位数的整数倍)。
由于被模除数是k+r位的,因此总共需要右移k位,即左添进尼个O,才能模除到最低位结束。得到的余数最多是r位(约定多项式为r+1位),再将它异或人一个新数据,作为新的被模除数。
每异或进一个数据,求新一轮CRC码,都只进行走(字节数据是一8)次的右移和一般都少于是次的模减(异或)运算,而且模减的中间差值无需保留(后值覆盖前值)。因此CRC码生成的运算过程,就是右移位、判断移出位为1则同多项式模减(C语言不能对移出位检测,需将余数备份后同0xol相“与”)、差值回存后再右移的是次循环过程,如图1所示。之后,再异或进下一个数据(该步与查表法一致)。编程得当的话运算量很小。
笔者用51汇编语言编写(2R(:一8校验程序,算得1字节数据的CRC码,只需64~80个机器周期,只多用1字节RAM单元(CR(:一16校验多用2字节,时间加倍)来存储余数,即下一次的被模除数(不断覆盖上一次已无用的)。因此,完全可以直接运算,而不必存储大量的数据表格。C语言编程,要考虑语句代码的优化以及只定义使用int和char型局部变量,以免耗时和占用RAM单元太多。
接收方对于最后收到的r位CRC校验码,不需要再纳入模除而使最终余数为O,只需同信息数据的模除余数比较,相等则确定通信正确。这样可以减少模除循环次数,节省时间。
3 硬件CRC校验的探讨
器件或设备的说明书中,常给出其硬件CRC码的生成电路。以总线数字温度传感器DS18820为例,其8位CRC码生成电路如图2所示。
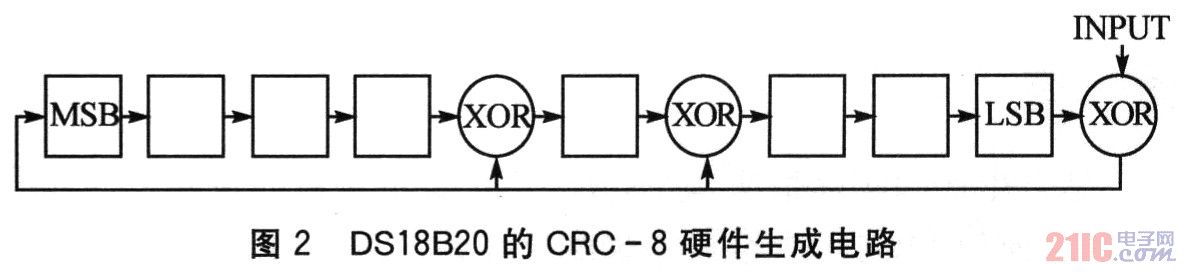
对应该硬件电路,等效的模除多项式为:
g(x)=x2+x5+x4+1
该模除多项式反序后,再隐含最高位,其多项式的值为8CH。
8位移位寄存器的初始值清O(00H),通信数组数据的每个字节低位在前,按位依次输入,当数据全部输入完成后,移位寄存器各个位的存储(输出)值就是所需的CRC校验码。
在实际应用中发现,Autonics等品牌的控制仪表,其通信CRC校验码与DSl8820的完全相同。
对应于图2的硬件生成电路,可用1片8D触发器(如74HC373)和1片4封装异或门(如74HCl36)连接而成,如图3所示。

对于CRC赋初值OOH(74HC373清O)的操作,可先读出DO~D7的随机值,然后将读出的数据再串行输入即可。因为相同的数据相异或总是为O,再除以任何多项式仍为O。
若MCU剩余足够的I/O口,可将CRC码的DO~D7位并行读入。否则,还需加一片74HCl65,将D0~D7转换成串行数据读入。
以少量的硬件实现快速CRC,能节省单片机的运算时间和存储资源。用于发送端,能够快速获得CRC校验码,在系统其他任务很重时,能增强实时性。而用于接收端,除了上述优点之外,还能显著增强系统接收和确认信息的可靠性,适用于一些远程控制的执行装置(如变频驱动器、阀门定位控制器、重要的监测报警装置等)。这些装置对于接收到的数据或命令信息,一旦因误校验而不能正确地判断执行,其后果都是比较严重的。因此,要提高嵌入式系统的可靠性和实时性,硬件CRC校验是一种选择。
结 语
本文在分析了常用CRC码的反序生成原理的基础上,给出了其编程运算的统一步骤,并提出了由硬件快速生成CRC码或对接收数据进行CRC校验的电路和方法,可为嵌入式系统的可靠性和实时性设计提供参考.

