摘 要： 介绍循环冗余校验title="CRC">CRC在TMS320C64x+系列DSP上的软件实现。 给出了该实现方法的理论推导过程并提供了相应的软件实现代码。
    关键词： CRC；DSP

 1 CRC常规实现方法
    CRC(Cyclic Redundancy Check)是一种广泛应用于各种通信系统的错误校验机制。例如，3GPP标准定义以下16位CRC校验多项式：
    G_CRC16(X)=X¹⁶+X¹²+X⁵+1
    CRC通常由硬件实现，图1说明由硬件移位寄存器实现的3GPP CRC16。

    图1中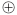，表示异或(XOR)运算, 异或运算在移位寄存器中的位置与生成多项式相对应。CRC运算前，移位寄存器清零，随后数据位被移入寄存器，当所有位都被移入寄存器后，寄存器的值即为CRC码。
    发送端将CRC码附在原始数据后发送；接收端用同样的方法为接收到的原始数据生成CRC码，并且与接收到的CRC码比较。如果不一致，则说明接收到的数据出错。
    CRC校验也可由软件实现，它比硬件实现灵活，但不如硬件实现效率高。假设变量crc代表移位寄存器的值，CRC16 软件实现的伪代码为：
    while(data_len--)
    {
      crc=(crc<<1)
      if (((input bit)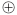(bit shifted out))==1)
         crc=crc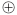0x1021           //0x1021 represents X¹²+X⁵+1
      else if (((input bit)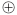(bit shifted out))==0)
      crc=crc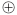0//this can be removed since it is meaningless
    }
    以上软件实现效率不高，主要是因为数据被逐个位处理，每次循环只能处理一位。一种常见的改进的软件实现方法可以每次循环处理一个字节，但它需要一个查找表。在查找表中保存所有的8位（一个字节）数据的CRC运算结果，因为8位数据有256个，所以查找表的长度为256。下面是生成查找表的伪代码：
    for(i=0；i<256；i++)
    crc_lut[i]=crc_value_for_one_byte(i)；//generate CRC for one byte
    用查找表方法实现的CRC16的代码如下：
    Uint16 crc16_lut(Uint8*data_prt，Int32 data_len，Uint16*crc_lut)
    {
      Uint8 crc_shift_out；
      Uint16 crc=0；
      while(data_len--)
      {
         crc_shift_out=(Uint8) (crc>>8)；//higher 8 bit of previous crc are shifted out
         crc=(crc<<8)^crc_lut[crc_shift_out^(*data_prt++)]；
      }
      return(crc)；
    }
    这个处理过程可被理解为：
    (1)计算移位寄存器在8个时钟周期中的输入：(crc_shift_out^*data_prt++)；
    (2)查找这个输入字节对应的CRC码：crc_lut[crc_shift_out^*data_prt++]；
    (3)把新输入数据的CRC码加到原有的CRC值上：(crc<<8)^crc_lut[crc_shift_out^*data_prt++]。
    在TMS320C64x DSP上，如果用这种方法实现CRC校验，每次循环大概需9个DSP时钟周期。而在TMS320C64x+DSP上新增了与CRC运算相关的Galois域乘法运算指令，使得每次循环仅需约1个DSP时钟周期。
2 C64x+DSP的Galois域乘法指令
    C64x+DSP系列是TI最新的高性能DSP系列，它有8个并行的运算单元，速度高达到1GHz。C64x+ DSP 提供了新的与CRC运算相关的Galois域乘法指令和寄存器，可在两个乘法单元M1、M2中并行执行。
    (1)GMPY：Galois域(32bit)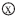(9bit)，寄存器GPLYA存放用于M1运算单元的多项式，寄存器GPLYB存放用于M2运算单元的多项式；
    (2)XORMPY：多项式为0的Galois域(32bit)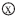(9bit)；
    (3)GMPY4：同时执行4个Galois域(8bit)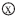(8bit)，M1和M2运算单元共用存放多项式的GFPGFR寄存器。
    注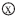：表示Galois域乘法。
    M1和M2可以并行执行，所以，C64x+每个时钟周期可执行2个(32bit)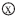(9bit)的GMPY或XORGMPY指令，或执行8个(8bit)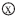(8bit)的GMPY指令。
    下面是C64x+GMPY指令的等效C代码：
    //32bits src1 multiply 9bit src2 with 32bit polynomial
    uint GMPY(uint src1，uint src2，uint polynomial)
    {
      uint pp；
      uint mask，tpp；
      uint i；
      pp=0；
      mask=0x00000100；//multiply by computing partial products.
      for (i=0；i<8；i++){
          if (src2 & mask) pp^=src1；
          mask>>=1；
          tpp=pp<<1；
          if(pp & 0x80000000) pp=polynomial^tpp；
          else pp=tpp；
      }
      if (src2 & 0x1) pp^=src1；
      return(pp)；//leave it asserted left.
    }
    请注意，这里的GMPY指令所用的多项式是GF(2³²)原多项式的低32位。例如：
    G(X)_CRC32=X³²+X²⁶+X²³+X²²+X¹⁶+X¹²+X¹¹+X¹⁰+X⁸+X⁷+X⁵+X⁴+X²+X¹+1
    用二进制数表示为：1 0000 0100 1100 0001 0001 1101 1011 0111=0x1 04c1 1db7，则GMPY多项式寄存器的值应该是0x04c11db7，没有必要包含最高位，因为它始终为1。GMPY所用的多项式必须是GF(2³²)域多项式，对于非GF(2³²)域的多项式，必须被左移得到32阶的多项式，并左移操作数src1，使它也是32阶，然后用GMPY指令运算，结果需右移同样的位数，从而得到最终结果。
    例如：Galois域G(X)=X⁸+X⁶+X⁵+X³+1(01101001)上的二进制数(01000001)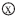(100)可以用以下方法计算：
    GMPY((01000001)<<24，(100)，(01101001)<<24)>>24
3 CRC在C64x+DSP上的高效实现
    比较CRC的软件实现代码和GMPY指令的等效C语言代码可以看出，一个字节的CRC码可以用GMPY指令计算为GMPY(polynomial, data_byte, polynomial)。
    用GMPY实现的CRC代码为：
      Uint32 crc_gmpy(Uint8*data_ptr，Int32 data_len_of_byte，Uint32 polynomial)
    //data_ptr is data pointer，data_len_of_byte is the data length in bytes
    {
      Int32 i；
      Uint32 crc32=0；
      GPLYA=polynomial；
      GPLYB=polynomial；
      for(i=0；i      {
              crc32=_gmpy(crc32，0x100)^_gmpy(polynomial，(*data_ptr++))；
      }
      return(crc32)；
    }
    以上代码中的“_gmpy”代表GMPY指令，用户按C语言函数调用的方式使用它，但DSP编译器会把它编译成一条GMPY指令，而不是一个函数调用。所有的C6000系列DSP指令都可以在C语音中按这种方式使用。
    以上代码在C64x+上执行，每次循环需要大约6个时钟周期，它比查找表方法效率高，而且不需要查找表，这对于存储器受限的应用来说非常合适。上述代码每个循环需要6个时钟周期的瓶颈因素是“循环依赖”，即下一次循环运算要基于前一次运算的结果，这使得C64x+指令流水线不能充分的流水式执行。一种改进的查找表方法可以解决这一问题，从而大大提高CRC计算的效率。该方法使用的查找表可以由以下代码生成：
    crc_lut[0]=polynomial；
    for(k=1；k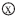         crc_lut[k]=_gmpy(crc_lut[k-1]，0x100))；//polynomialx8
    这种CRC的计算方法可用以下伪代码表示：
    Index=length_of_byte-1；
    for(k=0；k         crc=crc^_gmpy(crc_lut[Index--]，data_byte[k]))；
    为了更充分地利用C64x+ DSP并行流水式处理的能力，并减少查找表的长度，可以进一步对以上计算进行优化，每次循环处理32bit。相应的查找表长度减少为原来的1/4。查找表的生成代码如下：
    crc_lut[0]=polynomial；
    for(k=1；k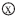        crc_lut[k]=_gmpy(_gmpy(_gmpy(_gmpy(crc_lut[k-1]，0x100)，0x100)，0x100)，0x100)；//polynomialx³²
    该方法的CRC计算可用以下伪代码表示：
    Index=length_of_word-1；
    for(j=0；j    {
        LutXn=crc_lut[Index--]；
        crc0=crc0^_gmpy(LutXn，data_byte[4*j])；
        crc1=crc1^_gmpy(LutXn，data_byte[4*j+1])；
        crc2=crc2^_gmpy(LutXn，data_byte[4*j+2])；
        crc3=crc3^_gmpy(LutXn，data_byte[4*j+3])；
    }
    //crc0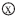x24
    crc0=_gmpy(crc0，0x100)；
    crc0=_gmpy(crc0，0x100)；
    crc0=_gmpy(crc0，0x100)；
    //crc1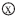x16
    crc1= _gmpy(crc1, 0x100);
    crc1= _gmpy(crc1, 0x100);
    //crc2x8
    crc2=_gmpy(crc2，0x100)；
    crc=crc0^crc1^crc2^crc3；
    上述基于GMPY和查找表的CRC优化实现，每次循环约需4个时钟周期，而一次循环处理4字节，所以每个字节的处理仅需约一个时钟周期。
    CRC是常用的检错机制，表1总结了几种CRC的软件实现方法在C64x+DSP上执行的效率。

    通过表1可以看出，在C64x+DSP上利用Galois域乘法指令极大地提高了CRC运算的效率。