摘  要: 太阳光发电作为洁净的和未来最有希望的发电方式之一，越来越受到人们的重视。光伏发电系统各个方面的研究都在不断地深入进行着，本文讨论的太阳光发电系统的最大功率点跟踪控制就是其中一个重要的研究课题。从实际应用角度出发，详细论述了采用功率对电压微分法进行最大功率点跟踪控制的过程，并通过实验验证其可行性和有效性。

　　关键词: 太阳能电池  太阳光发电系统  最大功率点跟踪  升压电路

　　太阳能电池的最大功率点跟踪控制是为充分利用太阳能，使太阳能电池始终输出最大电功率的控制，有登山法、功率数学模型法等。功率数学模型法是建立功率对占空比的数学模型，当日射量和温度有变化时要重新求得数学模型的参数，通过改变占空比达到最大功率点。因为是用4次方程定义功率对占空比的特性曲线，所以有一定的近似程度。登山法是最常用的控制法，通常的登山法是在最大功率点附近逐点计算、比较功率值来寻找最大功率点。当日射强度和温度急剧变化时，太阳能电池的输出特性也会有相应的变化，这就造成最大功率点的快速跟踪难以实现。

　　本文介绍的登山法在太阳能电池的输出特性有变化时也能快速地到达最大功率点。此控制系统以阻性负载的独立运行太阳光发电系统为基础，根据太阳能电池的输出功率对电压微分在最大功率点必然是0这一原理实现最大功率点跟踪控制。这种微分控制法，可以不考虑辐射强度和太阳能电池的温度变化对控制的直接影响。把导出的非线性状态方程经线性化处理后，将检测出的太阳能电池的输出功率和电压值代入求解，计算其微分及误差，然后根据误差结果通过自动控制使上述微分值始终趋向和保持为0。由此可见，如何高精度、快速地求得太阳能电池的输出功率对电压的微分是问题的关键所在。本文从对状态方程的分析，得出了改变斩波器的占空比就可以改变太阳能电池的输出电压的结论，然后利用太阳能电池在最大功率点的输出功率对电压微分是0的原理进行控制。

1 太阳光发电系统

1.1 系统构成

　　图1为纯电阻负载的太阳光发电控制系统。本系统实现最大功率控制的斩波器由电容C_S、电感L_C、功率开关T_C、二极管D_C以及滤波电容C_d构成。其中与太阳能电池并联的滤波电容C_S为斩波器产生的高频电流提供通路，以确保太阳能电池保持近似稳态电流输出，这样就可以不考虑太阳能电池的滞后性，而仅通过改变功率开关的开通占空比来进行最大功率控制。

1.2 太阳能电池的输出特性

　　太阳能电池的电压-电流(e_s-i_s)特性在忽略太阳能电池内部小的串联和并联电阻以后可以表示为:

式中，I_PH是太阳能电池的短路电流，I₀为二极管反向饱和电流，q为电子电荷，K为波耳兹曼常数，T是绝对温度。

　　图2是太阳能电池的es-is特性随日射强度和温度变化的关系。由图可见，e_s-i_s特性是非线性的，并存在最大功率点，而且最大功率点也随日射强度和太阳能电池温度的变化而变动。因此，为获得太阳能电池最大输出，最大功率点跟踪是必要的。

1.3 太阳能电池的最大功率和功率对电压的微分的关系

　　太阳能电池输出功率P_S及功率对电压微分dP_s/de_s可由下式表示:

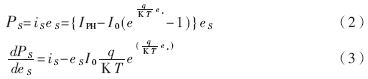
　　图3给出了日照1kW/m2、温度25℃时的功率特性，以及电压e_S与功率对电压的微分dP_S/de_S的关系。从dP_S/de_S和e_S的关系可见，太阳能电池在dP_S/de_S=0点发生最大功率，而且通过图2电压-电流特性曲线形状的一致性可知此结论在日射强度或温度变动时仍成立。因此，将dP_S/de_S=0作为控制目标，可以实现任何日射强度和任何温度时的最大功率点跟踪控制。这样，就把最大功率点跟踪控制转化为使太阳能电池的dPS/deS保持为0的定值控制问题。

2 以功率对电压的微分为基础的最大功率控制法

　　要用斩波器实现功率对电压的微分的最大功率控制法，在做计算时，首先要建立斩波器的数学模型，同时也要用到太阳能电池特性的数学模型。

2.1 数学表示式

　　假设TC是理想开关，根据电路分析基本原理，可以得到T_C在每一周期开、关两个状态的电路方程。

T_C导通时有:

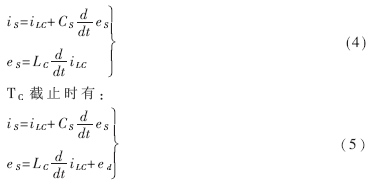
式中，i_LC是流过L_C的电流，e_d是斩波器的输出端的电压，斩波器占空比为D(0≤D≤1)。若在一个开关周期，将开关的状态量进行平均化处理，并用上划线表示状态平均量，则有:

　　在这个方程式中，i_S中含有e_S，因此是非线性的，最大功率点是该控制的平衡点。为简化计算，在平衡点附近进行线性化即可得到在平衡点附近的状态方程:

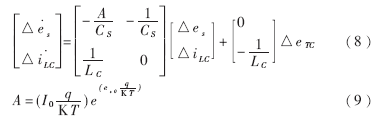
　　这里，e_s0即为太阳能电池PV的最大功率点工作电压。由于日射强度和温度的变化速度远远大于控制系统的跟踪控制速度，所以IPH、I0也可当作恒量处理，以便简化计算。

2.2 基于功率对电压的微分的最大功率控制

　　由图3可知，通过改变es或is的值可以控制太阳能电池的输出功率。在(8)式中，e_s是状态变量，而i_s不是，而且当L_C与C_d的值确定后，斩波器的斩波频率便可确定，es的改变主要由e_TC的变化决定。因此可知，调整eTC的大小可以改变es的值，并导致功率对电压的微分dP_s/de_s的改变。由前面的叙述可知，e_TC的大小可以通过改变占空比D来控制。因此，在上述条件下太阳能电池的工作点可以通过占空比D来控制。正确调整占空比D的大小可以实现dP_s/de_s为0的控制，从而实现太阳能电池输出的最大功率控制。

　　在实验中采用89C51单片机进行控制和计算，其P1.0端用于输出改变斩波器占空比D的振荡脉冲控制信号。用8bit 的AD0809作为模/数转换，在e_s值改变后，不断地检测改变了的工作点和dP_s/de_s值，使工作点趋近dP_s/de_s=0点。

2.3 最大功率点的确定

　　如何使用单片机进行控制，正确寻找最大功率点即dP_s/de_s为0的点是关键。这里，对dP_s/de_s的计算法进行说明。考虑在一定误差范围内简化计算，可近似得到dP_s/de_s如下:

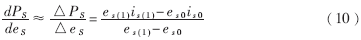
式中，e_s0、i_s0是前一次检测值，e_s(1)、i_s(1)是当前检测值。e_s、i_s的检测用固定的检测周期完成(实际实验中为100μs)。图4是寻找△P_S/△e_S=0点时的软件程序流程图，工作起始点D设定为0.5。当最大功率点电流小于0.5A时，停止最大功率跟踪控制。

3 实验结果

　　图1所示为实验电路图，实验中使用了意大利产的光伏电池阵列。为了保证电路工作稳定，首先通过实验对电感值进行确定，电感的大小直接影响MOSFET的工作状态和效率，同时也在一定程度上影响最大功率点的跟踪速度，因此要通过实验选定电感值，使MOSFET稳定工作，并在D不变时使太阳能电池输出功率相对较大。斩波器的斩波频率经计算和实验定为16kHz。A/D变换器AD0809的采样周期定为100μs。

3.1 启动时

　　控制开始前电容C_S、Cd由太阳能电池充电，其电压是太阳能电池的开路电压。其后斩波器启动，开始最大功率跟踪控制。开始时D为0.50，检测到的(△P_S/△e_S)0作为初始值，根据其正负决定D的增减方向，从而改变斩波器的D值，然后再对△P_S/△e_S进行检测，直到△P_S/△e_S等于零，即完成最大功率点跟踪控制。进行最大功率控制时的MOSFET栅极电压波形如图5所示。此时，占空比是0.655，太阳能电池PV输出电压为60.1V，输出电流为4.2A，输出功率为252.42W。开始工作es从开路电压很快达到最佳工作电压点，i_s从0到最佳工作电流点，PV输出功率也很快达到最大功率点，程序设计的时间约为8ms。得到的最大功率点与太阳能电池评价装置mp-140同时测的最大功率点相同。另外，达到最大功率点后，日射量不变则D基本不变，功率对电压的微分保持为0，即在最大功率点附近功率的波动非常小，达到较高的控制精度和稳定度。

3.2 日射量变动时

　　为了确认日射强度相对变动时的控制特性，采用遮光的办法，急速地改变太阳能电池阵列的输出功率，使PV输出功率从152.4W急速减小到87.5W，然后又急速增大到152.4W，观察其反应。实验结果是占空比很快由0.515变到0.582，然后又急速地回到0.515，功率很快达到最大功率点。由此可见，对于日射量的急变，控制器能够实现快速跟踪，具有较好的追踪、控制特性。

　　太阳能电池的最大功率点随着日射强度和表面温度的变化，时时刻刻在变动，但是太阳能电池的输出功率对电压微分在最大功率点始终为0。利用这个特性，通过恒值控制可以较好地实现最大功率跟踪控制。实验结果表明，这个最大功率控制系统对于日射量和温度大范围地变化具有高速、稳定跟踪特性，可以始终向系统的阻性负载提供最大功率。因此，可以确认此控制法是能够同时满足高速和高精度的最大功率控制法。

参考文献

1 董惠安.A Maximum Power Tracking Control Method for Photovoltaic Power Generation System  Based on Derivation of Output Power With Respect to Output Voltage. T.IEE Japan， Vol.118-D，No.12，98.114.843 

2 田中忠良.Study on Optimum Conditions for Maximizing Power Generation Obtained from PV Arrays. T.IEE Japan，Vol.118-B，No.11，98

3 高原健尔.An Adaptive Control Method for Maximum Power Tracking of Photovoltaic Power Generator. T.IEE

Japan Vol.118-D，No.6，98