摘  要: 提出一种有效的计算级联Z形码最小距离的方法。该方法将多维的级联Z形码并行地分成两个低维数的分量码，其中有一个分量码的维数固定为2，然后找出所有能在该二维分量码中产生低于某个已知的最小距离上限的输入序列，再验证这些序列在整个码中产生的距离，从而找出最小距离。从最后数字结果来看，使用普通的个人计算机，该方法能够在111小时内为码率为1/2的级联Z形码找出最小距离20，而在38小时内为码率为1/3的级联Z形码找到最小距离26。 

    关键词：  Z形码； 最小距离； 环； 联合界

    近来随着迭代译码技术的发展，许多具有非常优秀性能的码相继被发现^[1-2]。其中级联Z形码(Concatenated Zigzag Codes)就是一种非常优异而且编译码都简单的码，参考文献[3]中给出的一个码的性能离香农限仅0.9dB。 

    通常计算一个码的最小距离是一件非常困难的事。参考文献[3]中给出一种在一致交织器假设下计算级联Z形码的距离谱的算法。但该算法不适用于确定性交织器场合。错误脉冲法是非常有效的计算用迭代译码的码的最小距离的方法，如turbo码^[4]、LDPC码^[5]，但其缺点是不能保证计算结果的正确性。在参考文献[6]中，作者提出一种能够计算turbo码的真实最小距离的算法，参考文献[7]改进该算法，以增大计算的距离。本文提出一种利用环搜索来计算级联Z形码最小距离的有效方法。 

1 级联Z形码 

1.1  Z形码 

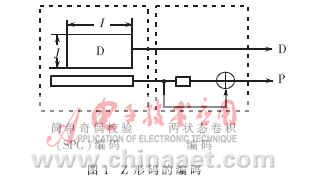
    图1描述Z形码的编码过程。首先信息序列被分成I段，每一段由J个比特组成。然后每一段做奇偶校验，产生一个奇偶比特，这个过程就是简单奇偶校验码(SPC)编码过程。然后这I个奇偶比特被送入一个只有两个状态的卷积编码器，进行卷积运算。使用d(i,j)i=1,2,…,I, j=1,2,…,J,来代表信息矩阵，则奇偶序列p(i)i=1,2,…,I可以用如下的公式来产生： 

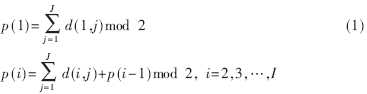
1.2 级联Z形码 

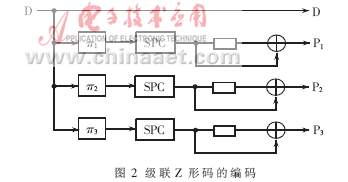
    一个K维的级联Z形码由并行的K个Z形码和K个交织器组成，见图2。其稀疏奇偶校验矩阵可以用如下式来表示： 

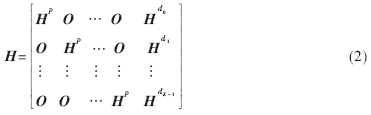
    这里H^p是一个I×I的双对角矩阵，O是一个I×I的全零矩阵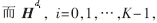，是一个I×IJ的稀疏矩阵, 该矩阵中“1” 的位置是由第i个交织器决定的。 

2  一个有效的计算最小距离算法 

    为了方便，将该算法分成当级联Z形码维数为2维和大于2维的两种情况。 

2.1  二维级联Z形码 

    对于一个二维的级联Z形码，假设输入重量为2w，根据Z形码编码原理，如图3所示，按顺序每两个“1”之间(用虚线表示)在每一个分量码中所跨过奇偶重量之和就是该输入序列产生奇偶校验总重量p。即: 

    这时产生的码字的总重量就是2w+p。值得注意的是，根据Z形码的编码规则，输入重量为奇数的序列产生的奇偶校验序列，相当于在输入序列最后插入一个“1”，因而输入重量为奇数的序列可以转换为输入重量为偶数的序列来考虑。另一方面，当级联码的维数只有2维时，图中虚线和实线(代表交织关系)将沿着箭头所指的方向形成一个闭环(图3(a)），或多个闭环(图3(b)）。 

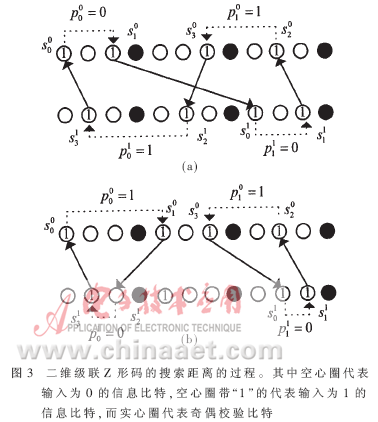
    一个简单的搜索单闭环的方法如图3(a)所示。首先在第一个Z形码中选择一个起始点s₀⁰，然后再在这个分量码中选另一个点s₁⁰，使得该点与s₀⁰之间的奇偶重量为一个确定的值p₀⁰，显然如果p₀⁰不为零，满足这个条件的点s₁⁰有2J种；而如果p₀⁰为零，就只有J-1种。然后s₁⁰被唯一地交织到另一个分量码上一个位置s₀¹。然后再在这个分量码中选一个点s₁¹，使得该点与s₀¹之间的奇偶重量为p₀¹。接着s₁¹又被唯一地逆交织到第一个分量码中的一个新位置s₂⁰。这样过程不断进行下去直到最后一个点s₃¹被确定。如果最后s₃¹逆交织到第一个分量码的点刚好是s₀⁰，则形成了一个闭环，该环中总的奇偶重量就为p。对于多环，如图3(b)所示，可用同样的方法得到每一个环，他们的总的奇偶重量就是p。 

    这样计算最小距离的过程如下： 

    假设已知最小距离的一个上限为d^*。就要找出所有能够满足d^*≥2w+p的w和p，而对于每一个p，还要找出所有满足(3)式的p_i^t，然后根据前面介绍的方法搜索单环和多环。 

    这样就能找出所有能产生小于和等于d^*的输入序列，因而就能找出最小距离d_m。值得注意的是，所有搜索到输入序列产生的距离都是一个最小距离的上限，因而都可以作为d^*，所以如果起初不知道d^*，可以设一个很大的值，比如N，然后再在搜索过程中利用搜索到输入序列中产生的最小距离作为d^*，使d^*不断地逼进d_m。 

    下面分析寻找一个输入重量为2w而奇偶重量为p的环所需要的计算量。 

2.2  寻找一个环长为p的单环的复杂度分析 

    我们知道，给定一个值p，能满足(3)式的p_i^t的数目共有: 

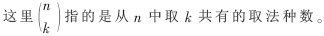    而对应(3)式中，如果有λ(λ≤min(2w,p)个非零的p_i^t，则在N_p中，满足这种情况的组合数为: 

    而另一方面，对于每一个确定的p_i^t的分布，如果p_i^t中非零的数有λ个，这种情况下，搜索一个环的复杂度为(2J)^λ(J-1)2^w-λ。这样当给定w和p后，对于每一个确定的起始点，搜索所有的单环复杂度为: 

    从这个结果来看，该算法能够非常有效地降低计算最小距离的复杂度。 

2.3  K-维级联Z形码(K>2) 

    当级联Z形码的维数K超过2时，将这K维码分成两个分量码，其维数分别为2维和K-2维。为了方便讨论，把2维的分量码叫做基本分量码，而把K-2维的分量码称为导出分量码。其方法是先在基本分量码中找出所有能产生距离小于或等于d^*的输入序列，然后再检查这些输入序列在整个K维的级联Z形码产生的总距离，这样即可找到所有能产生小于和等于d_m的输入序列。 

    注意，如果计算时间不受约束，该算法一定能找出真实的最小距离和所有产生该最小距离的输入序列；而如果计算时间有限，则该算法只能找到最小距离的一个上限d^*。 

3 数字结果 

    下面对三个码来计算其真实最小距离。这三个码的码长分别为504、1 008和480，前两个码的码率为1/2，最后一个码率为1/3。最终计算出的最小距离被列在表1中。其中第一个码的最小距离由输入重量为4、12、14三种序列产生，第二个码的最小距离由输入重量16的序列产生，而第三个码最小距离由输入重量为4的序列产生的。表1还给出了找出每一个码最小距离所需要的时间。所用的计算机为普通奔腾4个人计算机，主频为2GHz。 

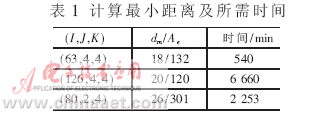
    图4给出了这三个码的BER性能仿真结果以及近似的联合界结果。该仿真采用的译码器为参考文献[8]中给出的APP算法，最大迭代次数为100。而近似联合界计算由(8)式给出^[6]: 

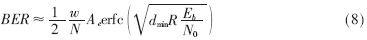
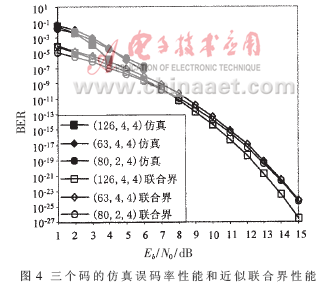
    其中R为码率，E_b/N₀为每一个比特的信噪比。从图4中可看出，随着信噪比的增加，近似联合界越来越接近仿真结果，它们都能很好地反映一个码在高信噪比时的误码率性能。 

    本文提出一种有效的计算级联Z形码最小距离的方法。从其中的数字结果来看，使用普通的个人计算机，该方法能够在111小时内为码率为1/2的级联Z形码找出最小距离20，而在38小时内为码率为1/3的级联Z形码找到最小距离26。最后利用最小距离来计算近似联合界，通过与误码率的仿真结果对比，近似联合界很好地反映了码在高信噪比时的性能，从而为评估码的性能提供一种有效的手段。 

参考文献 

[1] BERROU C, GLAVIEUX A, THITIMAJSHIMA P. Near shannon limit error-correcting coding and decoding: turbo codes [C]// Proc IEEE Int Conf Communications.Geneve, Switzerland: IEEE Press. 1993: 1064-1070. 

[2] MACKAY D J C, NEAL R M. Near shannon limit performance of low density parity check codes [J]. IEE lectron Lett, 1996,32(18):1645-1646. 

[3] LI P, HUANG X L, PHAMDO N. Zigzag codes and concatenated zigzag codes[J]. IEEE Trans Inform Theory, 2001,47(2):800-807. 

[4] BERROU C, VATON S, JEZEQUEL M, et al. Computing the minimum distance of linear codes by the error impulse method[C]// Proc IEEE Global Telecommunications Conference. Taipei, Taiwan: IEEE Press, 2002:1017-1020. 

[5] HU X Y, FOSSORIER M P C, EELFTHEROU E. On the computation of the minimum distance of low-density parity-check codes [C]// Proc. 2004 IEEE Int Conf  Communications. Paris, France: IEEE Press, 2004: 767-771. 

[6] GARELLO R, PIERLEONI P, BENEDETTO S. Computing the free distance of turbo codes and serially concatenated codes with Interleavers: algorithms and applications[J]. IEEE Journal on Selected Areas in Communications, 2001,19(5):800-812. 

[7] Ould-Cheikh-Mouhamedou Y,CROZIER S, KABAL P.Efficient distance measurement method for turbo codes that use structured interleavers[J]. IEEE Commun. Lett,2006,10(6):477-479. 

[8] LI P. Modified turbo codes with low decoding complexity[J].IEE Electron. Lett., 1998,34(23):2228-2229.