随着通信、雷达等技术的发展，软件无线电技术已经被广泛的用于无线基站、雷达信号处理、军用电台等多个领域。数字下变频技术作为软件无线电技术的重要组成部分，主要完成中频信号数模转换后的变频、滤波以及重采样等工作。数字下变频的主要硬件框图如图1所示[1]。

    根据不同的性能需求，滤波器组中采用以FIR滤波器为主，与梳状(CIC)滤波器、半带(HB)滤波器相互搭配来实现数字中频信号的抽取与滤波。梳状滤波器和半带滤波器通常用于前级的抽取滤波，以将信号速度降低到一定程度。整个信道波形的整形则主要依靠FIR滤波器完成。随着对信号处理精度和速度的要求不断提高，设计并实现更高速度和更高阶数的FIR滤波器成为推进数字下变频继续发展所需要克服的难题。目前国内很多论文发表FIR滤波器多为11阶[2]、16阶[3]等低阶FIR滤波器，其滤波效果很难满足实际需要。本文设计一种用于数字下变频的256阶分布式FIR滤波，并针对Cyclone III系列FPGA设计了合理的实现方法。
1 分布式算法分析
    FIR滤波器的表达式可以写为：
    
其中hk为滤波器抽头系数， xk为输入数据。式(1)中K的大小表征了FIR滤波器的阶数。如果采用通常的乘加算法来实现FIR滤波器，K阶滤波器需要使用K个嵌入式乘加单元。即使采用预加的实现方式也至少需要K/2个嵌入式乘加单元[4]。因此采用乘加算法直接实现高阶滤波器会消耗大量的嵌入式乘加单元。Cyclone III系列EP3C40F484C6N芯片上的嵌入式乘法单元仅为126个，直接使用硬件乘法器则FPGA片上资源无法满足要求。
    
2 分布式算法的变形与资源消耗推算
    从式(7)可知yB可能的取值与滤波器的阶数K有关，因此256阶滤波器至少需要2256个存储单元。从式(6)可知，如果xk的位宽为N，则yN的值需要经过N次移位相加后得到。若取N为24，则计算一个滤波结果需要完成24次移位相加。如果直接在FPGA上实现分布式算法，存储器资源和运算速度均无法满足需求，需要从滤波器阶数和输入数据位宽两方面对式(4)进行变形以减少存储器资源的消耗并提高运算速度。
    若N位的xk位宽划分为m段，每段L个比特，则可将式(4)变形为：
  
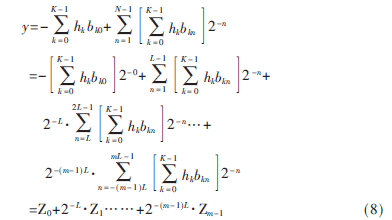
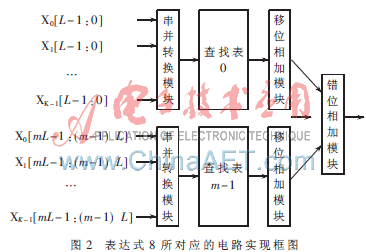
    从式(8)可以看出求得Zn（n=0，1，2…，m-1）的值仅需要进行L次移位相加运算，其运算时间是未变形前的1/m。但变形后需要同时使用m个查找表来并行完成查表运算。变形后所对应的硬件实现框图如图2所示。
    从图2可知式(8)所对应的实现电路主要由串并转换模块、查找表、移位相加模块以及错位相加模块组成。串并转换模块将x0～xK-1对应位串行移出组合后作为查找表的输入。查找表预先把所有可能的运算结果预存，根据输入数据查表直接求得滤波结果。移位相加模块完成查表输出的移位相加，求得表达式(8)中的Zn（n=0，1，2…，m-1）。最后根据Zn（n=0，1，2……，m-1）的权值不同，将其错位相加后可得到最终结果。

    查找表的大小由滤波器阶数决定，因此可通过将将式(4)变形为多个子滤波器级联的形式。通过减少各个子滤波器的阶数来减少查找表的大小，最后将各个子滤波器的结果求和可得到最终的滤波输出。可将式(4)改写为：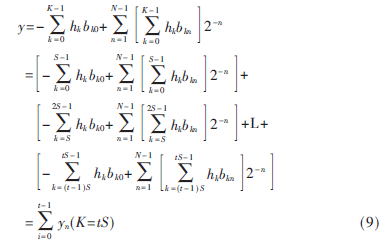

    从式(9)可知，可以将K阶FIR滤波器分解为t个S阶的子滤波器。其实现框图如图3所示。

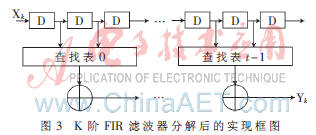
    由此可知每个子滤波器所需查找表的大小为2S，则划分为t个子滤波器后相比于未划分之前的所需的存储单元数量之比M0为：

    由此可知若将K阶滤波器划分为多个子滤波器可以让所需的储存单元成指数级降低，而为提高速度所增加存储单元只成线性增长。因此根据FIR速度和FPGA上资源的情况设计合理的实现方案到达速度和资源上的平衡。
3 FPGA实现方案及结果分析
    嵌入式存储器块是现代FPGA中常见的资源，嵌入式存储器块可以配置成不同大小和不同位宽存储器。Cyclone III系列的FPGA中嵌入的存储器块为M9K，每一个嵌入式存储器块容量为9 Kbit。M9K存储器可以根据需求被配置为8 192×1、4 096×2、1 024×9、256×32等多种形式。
    采用嵌入式存储器块来实现查找表，需要权衡子滤波器的阶数以及输出数据的精度。若考虑S阶滤波器中加法运算精度，则需其位宽扩展S-1位。对于系数为24位FIR滤波器而言，其子滤波器的查找表满足式(12)时可以将M9K的利用率发挥到最大。

    根据M9K嵌入式存储器的配置规格可求得S=8时为近似最优解，所以可将嵌入式存储器配置为256 × 32的模式，则每一个子滤波器为8阶。对于256阶FIR滤波器而言需要32个子滤波器级联而成，则总共需要嵌入式存储器块32个。为提高运算速度减少移位累加次数，根据公式(8)取m=3，则总共需要96个M9K嵌入式存储器，低于EP3C40F484C6N芯片所拥有的126个M9K嵌入式存储器的总数。
    根据前面所述设计RTL级代码并仿真，输入采用频率分别为50 kHz、2 MHz、8 MHz正弦混合信号仿真结果如图4。
    如图4所示50 kHz和2 MHz正弦信号被保留，而8 MHz正弦信号被滤除。

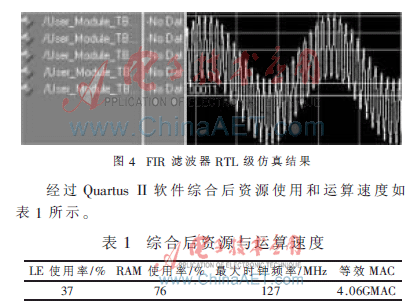
    由表1可知，在LE的使用率仅为37%时，RAM的使用率已达76%，还有较多的LE未被使用。可在随后的工作中进一步改进设计方案，采用超前进位加法等方法缩短关键路径，进一步提高滤波器的运算速度。
    本文对分布式滤波算法进行了详细的分析和推导，通过公式变形阐述了提高电路运算速度和减小存储器资源消耗的方法。通过理论推导和对Cyclone III系列的FPGA中嵌入的存储器块的分析，设计了一种适用于EP3C40F484C6N芯片的高阶分布式FIR滤波器实现方案并进行了仿真和综合。结果表明，采用该方案可以实现高阶的FIR滤波器设计并得到很高的等效乘加运算速度。

参考文献
[1] MALKI E S，SHEHATA K A，MADIAN A H.Design of  triple-mode digital down converter for WCDMA CDMA2000  and GSM of software defined radio.International Conference  on Microelectronics(ICM)，2009.
[2] 赵远鸿，宋学瑞.基于FPGA的数字下变频设计与实现[J].电子技术应用，2009，34(2).
[3] 魏灵，杨日杰，崔旭涛.基于分布式算法的数字滤波器设计[J].仪器仪表学报，2008(10).
[4] YOO H，ANDERSON D.Hardware-efficient distributed arithmetic architecture for high-order digital filters.IEEE International Conference on Acoustics，Speech，and Signal Processing(ICASSP′05)，2005，5：125-128.