摘要:基于提高速度和减少面积的理念,对传统的FIR数字滤波器进行改良。考虑到FPGA的实现特点,研究并设计了采用Radix-2的Booth算法乘法器以及结合了CSA加法器和树型结构的快速加法器,并成功应用于FIR数字滤波器的设计中。滤波器的系数由Matlab设计产生。仿真和综合结果表明,Booth算法乘法器和CSA算法加法器树,在满足FIR数字滤波器的性能要求的同时,在电路实现面积上、尤其是速度上有明显的优化;并且当数据量越多时,优化也越明显。
关键词:Matlab;Booth算法;CSA算法;ISE
研究数字滤波器的意义就在于它们正日益成为一种主要的DSP(DigitaI Signal Processing)运算,并正在逐渐代替传统的模拟滤波器。它可以保证任意幅频特性的同时具有严格的线性相频特性。而现场可编程门阵列(Field Programmable Gate Array,FPGA)可并行执行的特点决定它更加广泛地应用于实时数字信号处理领域。不能想象今天的生活如果没有音频;视频和言语交际的样子,而这些都要应用数字信号处理技术。并且在任何时候,高性能,低规模,低成本都是设计的目标。滤波器(Finite Impulse Response,FIR)的实现方法有很多种,最常见的有串行结构和并行结构方法。前者根据FIR滤波器的实现表达式,将滤波器实质看作是做一个乘累加运算。一次乘累加运算的次数由滤波器的阶数来决定。这种方法使用硬件资源相对较少,但速度较慢。并行结构的方法,将滤波器的串行实现展开,就可以直接用多个乘法器和加法器并行实现,其可以在一个时钟周期内完成一次滤波,但要占用大量的乘累加器,器件延迟比较大。目前为了满足面积和速度的需要,人们通常采用Booth算法、CSD算法,分布式算法等技术对FIR设计进行优化,优化效果各有利弊。本文针对串行结构对乘累加运算的乘和加分
别进行优化设计。分析了提高乘法器速度的途径;针对多数据量的运算,提出了一种新型的快速加法器的解决方案。体现了优化设计中提高速度和减小面积的设计理念。同时给出并实现了一个16阶FIR的设计实例。
1 用Matlab设计滤波器系数
利用Matlab软件的FDATool模块,选择滤波器类型为低通FIR,设计方法为窗口法,阶数为16,窗口类型为Kaiser,数据采样频率fs为4.8 kHz,滤波器的截止频率fc为1.08 kHz,导出的滤波器系数为16个15位的小数。将每一个系数扩大相同的倍数,最后四舍五人得到一系列整数系数。如下:
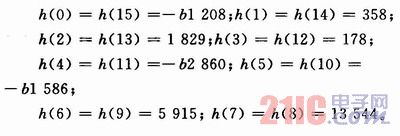
2 优化FIR滤波器在FPGA中的实现结构
2.1 FIR滤波器的基本算法原理
本文采用滤波器实现的基本的串行乘累加结构。FIR滤波器的差分方程可表示为:
![]()
式中:t为滤波器的阶数。
其直接运算结构如图1所示。
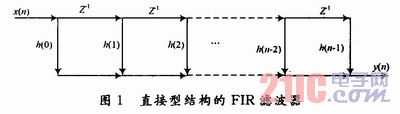
从公式(1)中可知FIR滤波器在硬件上的设计主要是完成乘累加功能,实现的一种方法是直接相乘累加。在实际应用中,当滤波器设计对滤波速度要求不高时,可采用串行结构或改进串行结构来实现,这样可以选取资源较少的器件,降低设计成本;当对滤波速度有较高要求时,可以考虑采用并行或DA来实现。但要进行FIR运算,尤其在阶数较高时,几乎无法在FPGA内实现并行结构,所以这里采用串行运算的结构,仅使用一个乘加器。所以本文的设计着重于提高串行结构FIR的速度。下面将介绍一种高速的Booth算法乘法器和高速的加法器。
2.2 乘法器设计
乘法器是数字信号处理电路中最常用的单元,20年前就已经研究的非常成熟。高性能乘法器是实现高性能的FIR运算的关键,乘法器的运算过程可以分解为部分积的产生和部分积的相加2个步骤。部分积的产生非常简单,实现速度较快;而部分积相加的过程是多个二进制数的相加,实现速度通常较慢。解决乘法器速度问题,需要减小部分积的个数、提高部分积相加运算的速度。在乘法器设计上这里着重研究能够减少部分积的Booth算法。
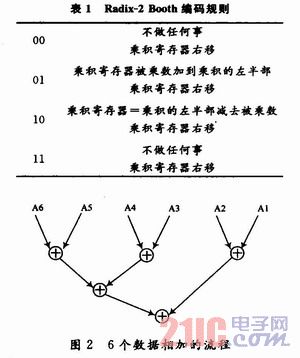
Booth算法乘法器可以减少乘法运算部分积个数,提高乘法运算的速度。本文讨论Radix-2的Booth算法,其基本算法思想是,一次看乘数的两个位,依照当前与前一位的不同,执行不同的操作。总结出Radix-2 Booth算法的编码规则如表1所示。
2.3 累加器设计
对于乘累加运算的加法,传统的算法将使多个乘法器的结果逐一累加,效率低、运算时延大。本文提出了一种结合了CSA算法加法器和树型结构的新型加法器结构,对乘法器的结果一次性相加。
图2为6个数相加的实例。如果不用其他加法器的话,6个数据的相加将耗去5个加法器,其关键路径总共经过三级的加法电路延迟,有必要对电路的面积和延迟进行改进。因此在多个数据相加的情况下,CSA(Carry Save Adder)加法器是很好的选择。
CSA加法器仍然保留原有的全加器架构,一个n-bit的CSA器件如图3所示。

如果只有个数不多的数据相加时,采用CSA器件不管是在电路面积和时序特性上都没有优势。但当多个数据相加时,CSA加法器就能在电路面积和时序特性上体现出它的优越性。树型加法器结构的关键特性在于利用不规则的树形结构对所有的准备好输入数据的运算及时并行处理,大大节省了计算延时,尤其是在多个数相加的情况下;缺点是其逻辑结构形式不规整,在VLSI设计中对布局布线的影响较大。本文用CSA加法器为单元组成树型结构,设计出一种如图4所示的快速加法器结构。由CSA加法器树组成的树型加法器中调用5个CSA加法器和一个普通加法器。R(0)~R(15)为前一级乘法器的16个输出。在整个加法过程中,CSA加法器在电路实现上本身就具备快速、面积小的特点,再加上树型结构的特点,使整个加法器在实现速度上进一步提升。同时整个加法过程能够满足最严格的时序要求,因为CSA电路只在最后的时间内执行进位加法,也就是由构成树的最后一级的Normal Adder(进位加法器)执行进位加法。通常在大部分的应用上会有一段足够的时间允许执行进位加法的时间延迟。
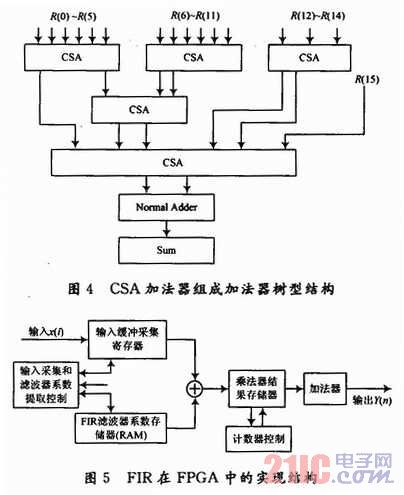
2.4 FIR在FPGA中的实现结构
本文设计的FIR在FPGA中的实现结构如图5所示,除了必须的乘法器和加法器外,还需要一个宽度为15、深度为16的滤波器系数存储器(ROM)和一个宽度为30、深度为16的乘结果存储器(RAM)。分别由相应的计数器控制模块控制,配合计数的值,执行相应的动作。针对输入的数据提取相应的滤波器参数,送入乘法器相乘,每得到一个结果送入下一级RAM中存储起来,最后统一送入加法器,一次性执行加运算并输出,最后得到滤波的结果。其中乘法器和加法器处理的都为符号数。
3 16阶FIR的设计及仿真结果
设计一个16阶的15位FIR滤波器。设计语言使用Verilog。设计工具使用Xilinx ISE平台。FIR的输入和系数都为15位有符号数,乘法器的位数为30位,经加法器后得到的滤波器输出为38位有符号数。编写testbench对设计进行逻辑仿真,随机选取16个输入数据。配合前面有量化后的滤波器系数,即可进行行为级仿真。图6中,rst为复位信号,clk为系统时钟信号,din为输入数据,coe为滤波器系数,dout为输出信号,control为输出同步信号。由仿真结果看出最终滤波器的输出结果和预期的结果相一致。同时利用ISE自带的综合器SXT进行综合,器件选用Xilinx公司的3s400pq208—4。综合报告显示,滤波器最大的频率可达到143.328 MHz,达到高速目的。报告显现资源的使用相对较大,没有预期的理想。从RTL电路分析出在CSA构成的加法器树部分在面积上的优化还不够明显,这个问题将在以后的研究中进一步解决。
4 结语
本文以FIR在FPGA中的实现结构为基础,研究了提高乘法器性能的途径,并实现了Booth算法的乘法器,此算法保证高速的前提下,缩小了硬件规模,使得该乘法器的设计适合工程应用及科学计算,在加法器实现上提出了一种结合了CSA加法器和树型结构的新型实现结构。利用以上两部分,成功设计了一个16阶FIR滤波器,并且达到了高速的目的,但在实现面积上还有待优化。

