摘  要： 建立了一个锅炉燃烧系统稳态参数优化模型。该模型利用神经网络表示主要物理量之间的关系，在约束条件下反映锅炉的运行条件，优化目标是追求能源消耗量最小。给出了优化模型的罚函数法求解算法，介绍了该模型的结果同底层自动控制系统进行连接的方式，并给出了一个实际的应用例子。理论计算和实际使用表明该模型有相当的精度，可以显著提高系统的能源利用率。

　　关键词： 锅炉燃烧系统  稳态优化  神经网络  罚函数

　　锅炉燃烧系统的运行状态一直是人们关心的有关能源利用和环境保护的问题。由于锅炉燃烧过程中各个物理量之间存在着强非线性关系，不易得到系统的数学模型，给实现自动控制带来了困难。已有相当多的文献对锅炉燃烧系统的自动控制进行讨论，讨论的重点在两个方面，其一是追求运行的优化效果，许多自动控制的新理论都曾经在这个问题上进行过尝试^[3][4][7][8];其二是如何使得锅炉自动控制系统能够长时间稳定运行^[3～4]。

　　由于锅炉运行的绝大部分时间是处在稳定状态，影响锅炉燃烧系统节能效果的主要因素是它在稳定状态的工作是否良好。如果锅炉稳定在经济燃烧的状态，其经济指标就能得到保证。因此锅炉自动控制系统的任务就是要保证在各种扰动作用的情况下使系统调节在最优的状态^[2]。基于这个认识，本文将锅炉燃烧控制系统设计为二级控制系统，底层的控制系统回路保证各种主要指标稳定在设定值上，而设定值则由上一级的优化系统进行计算设置。

　　锅炉燃烧控制系统的底层控制回路的选择有多种方式。通过分析，本文针对主蒸汽压力、氧含量、炉膛负压三个主要参数实施自动控制，并着重解决控制系统设定值即锅炉稳态运行参数的优化问题。文中给出了锅炉燃烧系统稳态运行参数的模型和模型求解算法，利用前馈神经网络描述了锅炉燃烧系统中的主要物理量之间的关系，这些关系作为优化模型的约束条件，使得模型能够模拟锅炉的运行，从而可以获得较高精度的优化结果。整个系统的优化控制如图1所示。

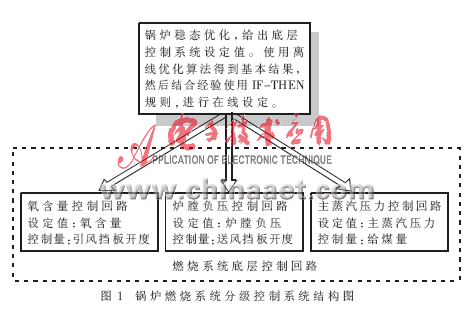
1 锅炉燃烧系统稳态优化模型

　　锅炉燃烧系统的主要物理量是给煤量、引风量、送风量、主蒸汽流量、主蒸汽压力、烟气氧含量以及炉膛负压等。从燃烧系统看，给煤量、引风量和送风量是系统的输入量，而烟气氧含量、炉膛负压是系统的输出量，主蒸汽流量是系统要适应的变化量，无法预先确定。锅炉燃烧系统稳态优化就是要确定合适的输入量，使得锅炉燃烧系统在提供足够的主蒸汽流量并保持主蒸汽压力恒定的条件下最经济燃烧，即使得燃烧系统的能源消耗最小。

锅炉稳态优化模型的形式化描述如下:

　　cl、c2、c3分别为送风量、引风量和给煤量的单位价格;x1、x2、x3分别为送风量、引风量和给煤量，是模型的决策变量;yl是蒸汽压力，它是x1、x2、x3和负荷的函数。函数f(x1，x2，x3，fh)是一个用BP神经网络表示的模型。

　　yf_min、yf_max分别表示引风量的最小、最大限制

　　sf_min、sf_max分别表示送风量的最大、最小限制

　　mei_min、mei_max分别表示给煤量的最小、最大限制

　　yl_min、yl_max分别表示蒸汽压力的最小、最大限制

　　模型(1)的约束条件由两部分构成，其一是关于决策变量(给煤量、引风量和送风量)的范围约束，即式(1.2)～(1.4);其二是关于主蒸汽压力范围的约束，该约束在模型中的作用是模拟锅炉系统运行。在主蒸汽流量一定的情况下，选择决策变量的取值时要保证锅炉主蒸汽压力在一定范围内。

　　模型(1)是一个有约束的线性优化模型。为了求解，将其转换为如下形式:

　　模型(2)是一个无约束最小化问题，它将模型(1)的约束条件用罚函数的方式表现在目标函数中，罚函数系数Mi的取值将随着出现非可行解的次数增加。该模型的具体求解算法如下:

　　①取Mi(i=1，2，…8)初始值为1000，允许误差ε，k=1;

　　②求无约束极值问题模型(2)的最优解;

　　③若对某一个j(1≤j≤8)有-g_j(x₁，x₂，x₃，yl)≥ε，则取M_k+1=10×M_k，令k=k+1，转第②步，否则停止迭代。

　　模型②求解的结果，是在给定的主蒸汽流量下，使得锅炉主蒸汽压力稳定，同时使得锅炉燃烧系统消耗最小的给煤量、送风量、引风量的值，即锅炉燃烧系统稳态参数的优化值。

2 神经网络模型

　　在锅炉燃烧系统稳态优化中要用蒸汽压力恒定来表示锅炉的运行状态。而影响主蒸汽压力的因素很多，在燃烧系统方面主要是给煤量、送风量、引风量。在不同的负荷下(即不同的主蒸汽流量)，相同的燃烧系统输入产生的主蒸汽压力也是不同的，所以还要考虑主蒸汽流量的影响。

　　由于主蒸汽压力和给煤量、送风量、引风量以及主蒸汽流量的关系是一个非线性关系，本文采用一个四层BP神经网络来描述。具体的神经网络模型是一个4×10×10×1的前馈神经网络，第一层是输入层，第四层是输出层，第二和第三层是中间层。设第q层(q=1，2，3，4)的神经网络元的个数为n_q(n₁=4，n₂=10，n₃=10，n₄=1)，输入到第q层的第i个神经网络元的连接权系数为。该网络的输入/输出变换关系为:

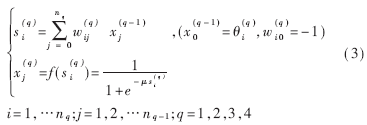
　　建立主蒸汽压力同主蒸汽流量、给煤量、送风量、引风量之间关系的模型就是要训练这个四层的BP神经网络，使得它的输入/输出关系满足实际的输入/输出关系。本文采用的训练方法为反向传播(Back Propagation)学习算法。采用BP神经网络的原因是它具有较好的泛化功能。具体的学习算法表示如下:

　　设给定P组输入输出样本为:

　　所谓神经网络的学习就是调整它的权重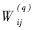，使得其代价函数最小。基本的BP算法可以表示成如下的形式:

　　上述基本算法的缺点是收敛速度慢、局部极小。对此可采用变步长方法改进收敛速度慢的问题。变步长方法的算法为:

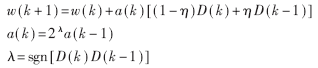
　　当连续两次迭代的梯度方向相同时，表明下降太慢，可增加学习率;如果学习率太大，连续两次梯度方向相反，表明修正过头，则减少学习率。

3 优化模型的应用及结论

　　本文对某厂一个75t/h的锅炉进行了建模。实际使用情况表明这个神经网络在建立主蒸汽压力模型时可达到相当高的精度。图2是实际测量值与模型估计值的残差，可见其误差很小。统计检验表明，估计值的均值与测量值的均值相等，误差的方差为0.0114。需要指出的是在进行神经网络训练时，要对训练数据进行无因子化处理。本文使用的无因子化方法是最大值去除法。

　　表1给出了在神经网络模型的基础上优化计算的结果。表2给出该厂两个月实际运行的耗煤量和优化计算估计的耗煤量。可以看出计算结果有大约6%左右的节能率。实际运行中操作人员按照我们优化结果做指导，节能率大约在2～3%。

　　表1中还给出了氧含量的估计值，这个值是在建立了一个描述氧含量与给煤量、送风量、引风量和主蒸汽流量之间关系的神经网络模型的基础上根据模型计算得到的。从该值的变化趋势看，显然同经验研究的结论是符合的，即当负荷(主蒸汽流量)下降时，为保证锅炉经济燃烧，其烟气氧含量要上升^[1]。

　　可通过再建立一个炉膛负压与给煤量、送风量、引风量和主蒸汽流量之间关系的神经网络模型，计算出最优的炉膛负压，再加上上面提到的氧含量，就可以确定底层控制系统的给定值了。具体实现方法是将优化结果和运行中的一些安全限幅要求结合起来，组成一个IF-THEN规则库，实时设定控制系统给定值。一个很有吸引力的思路是建立在线的神经网络辨识器，通过实时的模型辨识、优化，产生控制系统设定值，这是下一步的研究方向。

　　本文提出的锅炉燃烧系统稳态参数优化方法，可在基于锅炉正常工作数据建立系统模型的基础上比较容易地获得锅炉稳态运行的优化值。而锅炉燃烧系统稳态优化的结果又可以进一步用作为人工或者自动控制的参考值。实践表明该模型的结果符合实际生产情况，取得了显著的节能效果。

参考文献

1 金以慧， 方崇智.过程控制.北京:清华大学出版社，1989

2 Sehitoglu，H. Fire By Wire，Optimal Control of Boiler  Fuel Economy With Environmental and Safety Con-

strains.American Control Conference，1987

3 郑怀林， 叶 桦， 陈维南.工业锅炉燃烧系统分级智能控制.工业仪表与自动化装  置，1999(2)：16～18

4 石兆三.火电厂锅炉燃烧过程模糊控制系统的设计及应用.自动化仪表，1999(9)： 32~35

5 孙增圻.智能控制理论与技术.北京:清华大学出版社，1997

6 《运筹学》教材编写组.运筹学.北京:清华大学出版社，1990

7 郑德忠.实现锅炉优化燃烧的新型控制方案.自动化仪表，1998.3

8 周以琳.锅炉燃烧系统优化控制及实现方法.工业仪  表与自动化装置，1998.4