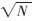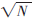摘  要： 在折半循环编码算法的基础上，提出了一种增加算法初始化节点数量和松弛正向差集的对称分布式互斥请求集生成算法，使算法的时间复杂度大幅度降低，而所生成的请求集长度仍然保持~2之间。
关键词： 松弛正向差集；请求集;折半循环编码算法

　基于请求集的分布式互斥算法作为Maekawa算法[1]的推广，近年来得到了人们的广泛关注，人们提出了许多各具特色的算法[2-5]来构建请求集以降低分布式互斥算法的消息复杂度或者提高分布式互斥算法在其他方面的性能。但在通常情况下，分布式互斥请求集生成算法的性能直接影响分布式互斥算法的性能。例如，请求集生成算法的对称性将影响分布式互斥算法的对称性，请求集生成算法所生成请求集的长度直接影响基于其上的分布式互斥算法的消息复杂度。而目前已经存在的分布式互斥请求集生成算法在请求集长度、时间复杂性等方面都不能让人满意。李美安[6]介绍了一种用循环编码产生请求集的互斥算法，它通过循环编码产生请求集的方式得出一种消息复杂度较低、容错性能高且同步时间短的对称分布式互斥算法。但由于李氏循环编码互斥算法的初始化节点数较少，因此算法的时间复杂度还是较高。
　为了在折半循环编码算法中改善请求集生成算法的性能，本文提出了一种通过提高请求集中初始化节点数量的算法[7]，虽然在算法中引入了对称请求集的概念，只须计算前「N/2]骎行和第0行有交点即可，空间复杂度可降低到O(N2/2)，比李美安提出的用循环编码产生请求集的互斥算法的空间复杂度提高了50%，但和参考文献[8]提出的一种基于循环的请求集产生算法的消息复杂度O(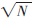)相比，还有较大的改进空间。因此本文在折半循环编码算法的基础上引入松弛正向差集的理论，提出了一种提高请求集初始化节点的数量和运用松弛正向差集的方式来改善请求集生成算法时间复杂度的算法，从而更快、更优地产生请求集，且易于实现。
1 系统模型
　设系统的节点数为N，并从0~N-1对节点编号，第i个节点的ID号为i-1，假定系统的节点与通信均可靠，各节点没有共享存储器和共同的物理时钟，节点间依靠消息进行异步通信，并且消息通信时间延迟无法预知。

　定理：循环请求集与松弛正向差集等价。
　循环编码算法中已经证明，循环编码所产生的请求集满足Maekawa所提出的4个条件，其产生的请求集是对称请求集，而在松弛差集算法中证明了循环请求集与松弛差集等价的定理，因此松弛循环差集所产生的请求集也是对称请求集。而本算法是在松弛差集算法的基础上进行的改进，即通过增加初始化请求集的长度，来缩短算法的时间复杂度，以求更快地找到所求请求集，因此本算法所产生的请求集也是对称请求集。
1.3 请求集初始化理论
　根据Maekawa在参考文献[1]中提出的请求集应满足的条件可知，系统的节点数(N)最少需要用长度为m的请求集表示(N<m(m-1)+1)，那么基于循环编码的请求集生成算法的请求集方阵中每行至少有一个1，并且每个1与码字的第0位的距离不相同。
　依据此条件考虑到2的幂之间的差的互异性，本算法在折半循环编码算法中再以2i+1-2i为间距对请求集方阵第0行请求集码字进行初始化。为了更好地优化循环基，令2k≤N/2，因为只有2k≤N/2时才能保证初始化节点的任意两点间的距离不等。比如对于10个节点的请求集为1101000100，由于第3个节点和第0个节点之间的距离与第7个节点和第0个节点之间的距离相同，为了使循环基也变成单向的，应使2k≤N/2，从而(2j-2i)mod N(i≠j且i，j∈k)之间的距离不等。为了减少循环编码的次数，本算法在折半循环编码算法的基础上引入松弛正向差集，即当(xj-xi)mod(N)(j>i)在小于N/2中的所有节点都可以表示时，此时的请求集即为所求的请求集。
综上所述，通过松弛正向差集的优化能更好地提高本算法的时间复杂度。



　本文在折半循环编码算法基础上，在提高循环编码初始化节点的数量和引进松弛正向差集的概念两方面进行合理的改进，使空间复杂度由O(N2/2)下降到O(N)，时间复杂度由O(N2/2)降到现在的O(N/2)，因此本算法易于实际应用。
参考文献
[1] MAEKAWA M. A 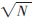algorithm for mutual exclusion in decentralized systems[J]. ACM Transactions Computer Systems， 1985， 3(2)：145-159.
[2] AGRAWAL D, ABBADI A E. An efficient and fault-tolerant solution for distributed mutual exclusion[J]. ACM Transactions  on Computer Systems， 1991， 9(1)：158-167.
[3] CHEUNG S Y， AMMAR M H. AHAMAD M. The grid protocol： a high performance scheme for maintaining replicated data [J]. IEEE Transactions on Knowledge and Data Eng，1992，12 (6)：42-53.
[4] KUMAR A. Hierarchical quorum consensus： a new algorithm for managing replicated data[J]. IEEE Transactions on Computer Systems， 1991，9(6)：996-1004.
[5] HARADA T， YAMASHITA M. Transversal merge operation： a no dominated coterie construction method for distributed mutual exclusion[J]. IEEE Transactions on Parallel and Distributed Systems， 2005， 2(2)：183-192.
[6] LI Meian. A high performance distributed mutual exclusion algorithm base on cyclic coding [J]. Acta Electronica Sinica on 2005， 33(8)：1397-1402.
[7] 陈志党，李美安.一种新的分布式互斥请求集生成算法[J].微计算机信息，2010(3-9)：211-212.
[8] LUK Waishing. Two new quorum based algorithms for distributed mutual exclusion[C]. Proceeding of the 17th International Conference on Distributed Computing Systems， IEEE， 1997： 100-106.