对流层散射通信是利用对流层中大气的不均匀性对超短波和短波的散射或反射作用来实现的一种超视距无线通信方式。该通信方式因传输容量大、单跳距离远、保密性能优越、抗毁性和抗干扰性强等特性成为军事通信中不可或缺的一部分，特别是其不受太阳黑子、磁暴、极光、雷电等影响，在军事通信中有着重要的战略意义[1]。其主要缺点在于多径散射信道下的信号传输损耗较大，衰落严重。多径干扰成为影响该通信性能的主要因素之一，限制了其更广泛的应用。而正交频分复用OFDM(Orthogonal Frequency Division Multiplexing)技术[2]，因其较高的频谱利用率和易于实现等特性而被广泛应用，特别是其能有效消除多径信道间干扰，在对流层散射通信中有着广泛的应用前景。
    为分析多径信道下对流层散射通信的性能，良好的信道估计是基础，很多文献对此进行了相关的研究和探讨。参考文献[3]对异步多用户OFDM系统的多径信道进行了半盲估计，参考文献[4-6]分别就多输入多输出多径信道中采用特征值分解的系统性能以及Ricean和Rayleigh信道下系统性能做了详细的分析，参考文献[7]分析了对流层散射通信中一种改进的SVD算法，一定程度上改善了系统性能。本文在上述文献的基础上，详细分析了对流层散射信道特性，设计了采用OFDM技术的多径散射信道系统模型，并对该条件下不同信道估计性能作了分析，对比仿真分析了不同算法和不同多径数目下的误码性能，给出了结论。
1 对流层散射信道衰落特性
    由于对流层的不稳定性，对流层散射信号电平随时间而随机变化，通信面临严重的深度衰落影响。其衰落特性主要分为慢衰落和快衰落，其中慢衰落指短期信号电平在以昼夜、月、季和年以至数年为周期的长期变化，而快衰落指瞬时信号电平在几分钟到一小时的短期变化[1]。

1.2 快衰落
    对流层散射通信中，由多径传输造成的信号快衰落是许多散射元相互干涉的结果，通过不同路径到达接收端的信号的相位、幅度和时延均不相同，当传输时延差?驻?子比传输的基带信号的持续时间T小得多时，多径传输对接收信号的影响仅表现为平坦快衰落。
    当经过不同传输路径到达接收端的信号支路数很大时，接收信号为一窄带高斯过程，合成的信号包络的概率分布服从Rayleigh分布，信号相位服从0~2π区间内的均匀分布。某一时间间隔内，信号瞬时振幅的概率密度函数p(V)和信号包络的概率分布函数P(V)分别为：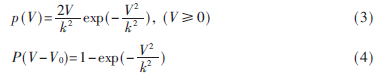

其中V为信号电平，k2为信号电平的均方值。快衰落的衰落速率随着时间、频率、地理环境等条件的不同而显著变化。
2 系统模型及信道估计算法
2.1 系统模型
    以OFDM技术为基础来建立对流层散射多径信道系统模型，模型简图如图1所示，略去了详细的OFDM信号处理过程，只列出了其关键步骤，其中CPI和CPD分别表示加入和删除循环前缀CP(Cyclic Prefix)。

    信源信号经过映射、编码等变换后，通过IFFT将信号调制到各个子载波上，插入足够消除符号间干扰的CP后从发射天线发射出去。从发射端发射的信号经过对流层散射信道，经历不同的路径达到接收端，在接收端完成解调、译码等步骤处理。其中，经过FFT解调并删除CP后对信号进行信道估计，以此来估计、分析多径散射信道的特性。
2.2 信道估计算法
    设收端信号为Y=XH+N，X为发端导频信号矩阵，H、N分别为信道矩阵和噪声矩阵。在信道估计后，为消除码间干扰，采用迫零均衡算法对系统进行均衡以补偿传输信道特性和降低系统误码。
    针对信道估计问题，本文主要讨论基于导频的信道估计方法，分析LS和LMMSE信道估计算法，同时将基于变换域的信道估计算法引入本文，分析该算法下系统性能。
    设各径信道为独立的服从Rayleigh衰落分布的多径散射信道，且各径信道衰落服从快衰落分布，则LS信道估计算法[8]为：

    为进一步降低MMSE算法的复杂度，另外采用一种改进的MMSE信道估计方法即基于DFT的变换域（Transform Domain）法对信道进行估计，其核心思想是通过DFT将信道估计问题在变换域中进行处理，以减少系统估计的运算量，提高系统估计精度[10]。变换域法是一种将变换域中的值看作频域信号的DFT，即与频域信号的“频域”对应的方法。下面分析基于DFT变换域的信道估计算法，其实现框图如图2所示[11]。

    接收端从导频信号中估计出多径信道特性HLS后，通过M点的DFT得到变换域的M点序列。在变换域中，

3 仿真分析
    对上述算法在对流层散射多径信道中的性能分析，OFDM系统的参数设置如表1所示。

    对于各散射多径信道的时延和Doppler频移两参数的设置，参考前期工程实际测量的数据，选取华北某地区一条300 km散射通信链路下的数据，其详细值如表2所示。

    根据上述分析和设置，采用OFDM技术的对流层散射多径系统，当多径数目为3时，不同信道估计算法对应的误码率和均方误差曲线分别如图3和图4所示。从图中可知，基于DFT变换域的信道估计算法下的误码性能略优于LMMSE算法，同时较大降低系统均方误差。在误码率为10-3数量级时，基于DFT变换域算法优于LS算法3 dB左右，优于LMMSE算法约0.5 dB。

    针对对流层散射不同多径数目条件下系统性能问题，本文采用基于DFT变换域的方法对系统进行仿真分析，其误码率和均方误差曲线分别如图5和图6所示。

    从图5、图6中可知，由于不存在多径间干扰，单径时误码率和均方误差均明显优于多径情况；多径情况下的均方误差没有明显的差异，误码率随着多径数目的增加呈明显上升趋势，当多径数目为7时高达10-2数量级，基本上不能满足系统要求。
    本文针对对流层散射多径信道的衰落特性，采用OFDM技术对该散射多径信道进行了系统建模仿真，对比分析了不同信道估计算法下系统的误码性能和采用基于DFT变换域法的系统在不同多径数目条件下的误码性能。仿真表明，基于DFT变换域算法的性能略优于LMMSE算法，明显优于LS算法；在不同多径数目条件下，为实现对流层散射信道的可靠通信，在适当地增加系统信噪比的同时，选择相对较少多径数目，有利于系统性能的提升。
参考文献
[1] 张明高.对流层散射传播[M].北京：电子工业出版社，2004.
[2] 陈西宏，刘强，胡茂凯.OFDM中基于粒子群优化的限幅算法[J].空军工程大学学报（自然科学版）,2010,11(2):52-56.
[3] JUNG H, ZOLTOWSKI M D. Semiblind multichannel identification in asynchronous multiuser OFDM systems[J].Thirty-Eighth Asilomar Conference on Signals, Systems and  Computers, 2004,1:692-696.
[4] COLLINGS I B, GAO Xi Qi, MCKAY M R,et al. MIMO multichannel beamforming: SER and outage using new eigenvalue distributions of complex noncentral Wishart matrices[J]. IEEE Transactions on Communications, 2008,56(3):424-434.
[5] GAO Xi Qi, WONG Kai Kit, MCKAY M R McKay, et al. MIMO multichannel beamforming in interference-limited  ricean fading channels[J]. IEEE Global Telecommunications Conference, 2008:1-5.
[6] SHI Jin, MCKAY M R, SUN Liang. MIMO multichannel  beamforming: analysis in the presence of rayleigh fading, unbalanced interference and noise[J]. IEEE GLOBECOM 2008,2008:1-5.
[7] 胡茂凯,陈西宏,刘斌. 对流层散射通信中基于改进SVD的信道估计算法[J].电讯技术，2009,49(8):69-72.
[8] Van de Beek J.-J., EDFORS O, SANDELL M. et al. On channel estimation in OFDM systems[J]. 1995 IEEE 45th  Vehicular Technology Conference, 1995, 2:815-819.
[9] NOH M,LEE Y, PARK H. Low complexity LMMSE channel estimation for OFDM.[J]. IEE Proc.Commun., 2006,153(5): 645-650.
[10] 张继东,郑宝玉.基于导频的OFDM信道估计及其研究进展[J].通信学报, 2003,11(24):116-123.
[11] ZHAO Yu Ping, HUANG Ai Ping. A novel channel estimation method for OFDM mobile communication systems  based on pilot signals and transform-domain processing[J]. IEEE 47th Vehicular Technology Conference, 1997,3:2089-2093.