自20世纪70年代被提出以来,预测控制相对传统PID控制的很多优势令其在工业过程应用中产生了重要和广泛的影响。预测控制的方法有很多种,例如:动态矩阵控制(DMC)、扩展的预测自适应控制(EPSAC)、模型算法控制(MAC)、预测函数控制(PFC)、二次动态矩阵控制(QDMC)、序贯开环最优控制(S0L0),以及广义预测控制(GPC)等,统称为"模型预测控制"(modelDredictive Control,MPC)。预测控制的基本原理类似于利用内部模型的状态或输出预测,同时应用有限预测时域的滚动计算思想和反馈及预测校正,最后采用了对某个系统性能指标的最优化计算,以确定在一个控制时域内的最优控制序列。本文通过数学推导为预测控制和PID控制建立起一种广义联系,并在此基础上,详细阐述了基于GPC的自适应PID控制器的设计方法,具体应用到了电站锅炉氧含量的自动控制上。
烟气氧含量的多少直接反映了燃烧状况,氧含量过低会造成燃烧不完全,既增加煤耗又污染环境。烟气氧含量同时也是环保的重要指标,氧含量过高会使送风机、引风机电耗增加,还会造成烟气中二氧化硫及氮氧化物排放量的增加。
锅炉烟气氧含量自动控制的目的是为了最大限度地实现燃烧的最优化,合理调整风煤比。许多电站机组的氧含量自动控制没能很好投入,其主要原因是由于氧含量自动控制系统参数优化不理想,在面对电站锅炉负荷变化,烟气氧含量设定值不同的情况时,控制系统不能快速跟踪设定值,甚至出现反复震荡的现象。本文采用的基于GPC的PID控制方法既可以克服传统定值PID的动态响应差的问题,而且具有一定的自适应特性,适合实时在线控制。
1 预测控制与PID控制的广义联系
1.1 PID控制法则
增量形式的PID控制法则描述如下:
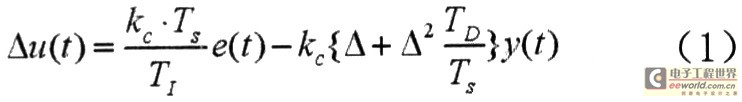
其中,

式中:u(t)、y(t)、w(t)分别为系统输入、输出信号和参考输入信号,kc、TI和TD分别为比例增益、积分时间常数和微分时间常数,Ts为采样时间,△=1-z-1为差分算子。
为方便计算,令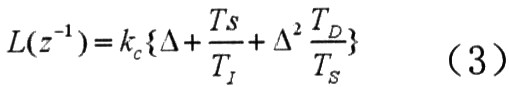
则式(1)可以表示为△u(t)、y(t)、w(t)的等式:
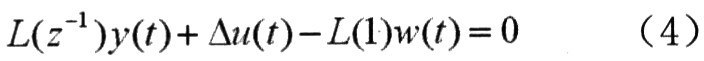
1.2 预测控制法则
虽然预测控制包括很多算法,但基本原理相同,它们采用二次型函数作为系统性能指标:

式中,Yd为期望输出向量,当不采用柔化方法时,直接令其为设定值向量;

为系统未来输出自由响应估计向量;
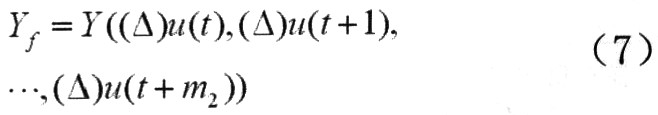
为系统未来输出强迫响应估计;

对J进行极小化,可求最优解为:

其中G为一系列矩阵已知的组合,这些矩阵都来自于对Yo和Yf的求取过程。
2 基于GPC的自适应PID控制器设计
2.1 GPC算法描述
广义预测控制(GPC)采用CARIMA模型描述被控对象:
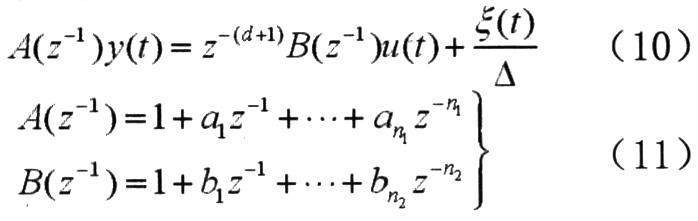
其中,
式中,ζ(t)为均值为0、方差为σ2的白噪声序列,d为系统延迟。
系统二次型性能指标函数为:
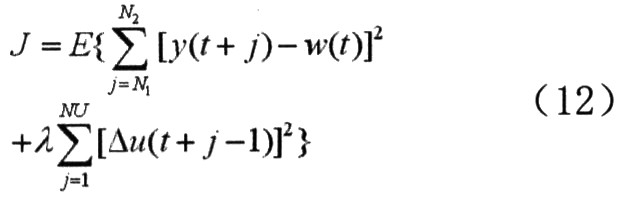
式中,入为控制增量加权因子,N1、N2、和NU分别为最小预测时域、最大预测时域和控制时域。为简化计算,通常令NI=1,N2=NU=N。
对式(12)J极小化后求得二次型性能指标函数的最优解为:
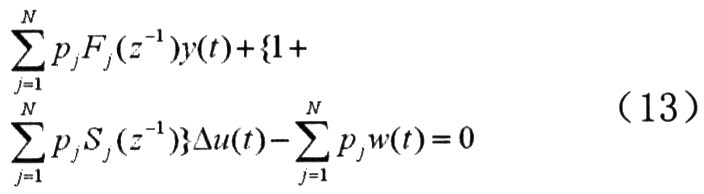
式中![]() 可通过如下丢番图方程计算:
可通过如下丢番图方程计算:
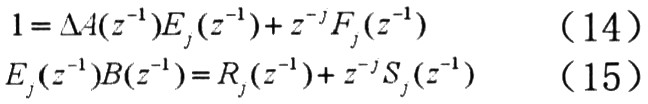
其中,
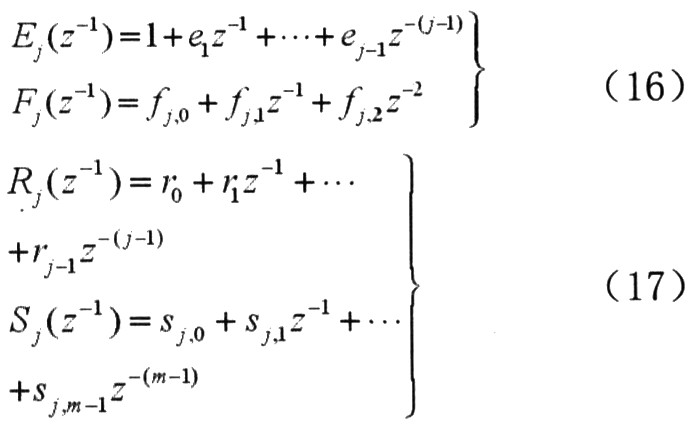
且P(z-1)被定义为:

其中Pj可由下式计算:
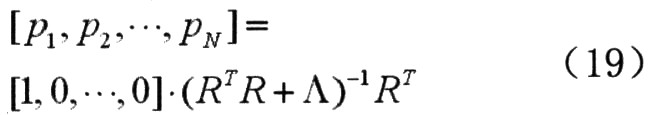
式中R阵由式(12)中的Rj(z-1)系数构成,
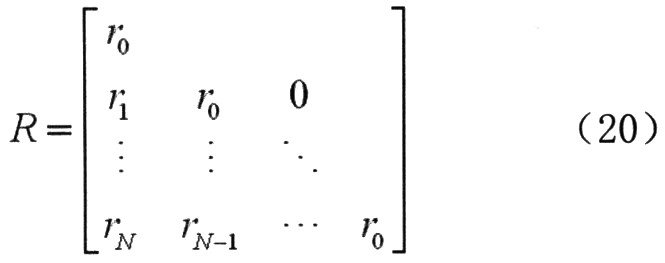
另外,A被定义为:

2.2 PID参数整定

其中,

如果下式
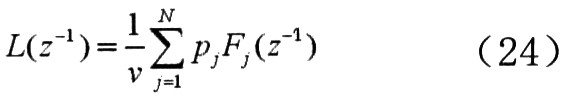
成立,那么式(22)与式(4)恒等,并且可以得到

其中,

2.3 系统模型参数辨识
对于式(11)中的多项式中的参数,可以通过下面的递推最小二乘算法得到。
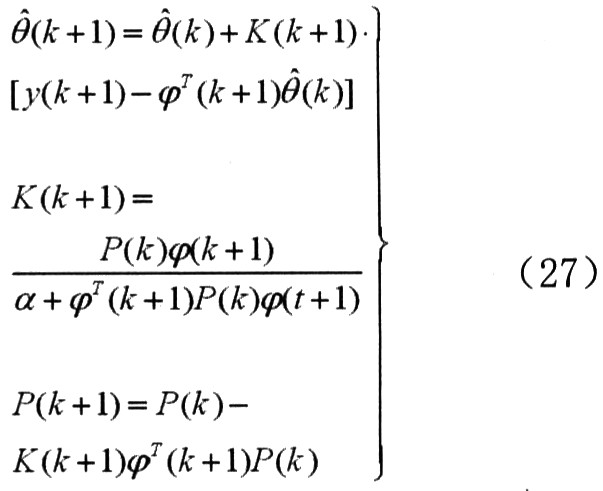
式中,α为遗忘因子,θ(k)为参数向量估计,ψ(k+1)为对应的数据向量。

3 仿真实例
将基于GPC的烟气氧含量PID控制器与定值PID控制器做MATLAB仿真比较:
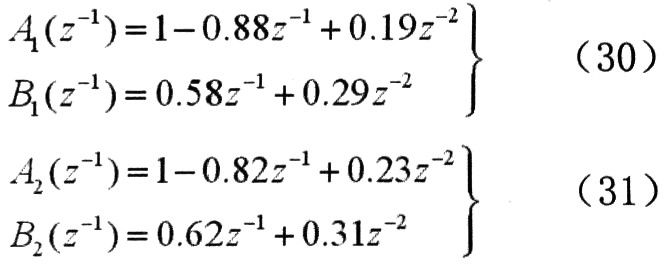
控制参数取值如下:λ=2,d=3,N=20 。当控制对象和设定值变化时,固定取值不再适合新的控制对象,如图1所示;而基于GPC的PID控制器能够在控制对象和设定值变化时调用控制算法,对新的控制对象PID参数进行调整,具有一定的自适应性,有效地减小了超调和响应时间,如图2所示。

4 结论
本文讨论了预测控制律与PID控制律之间的对应关系,通过一个实际的例子(基于GPC的PID控制器设计)得出PID控制器的参数。仿真结果表明了文中所提出方法适用于火电锅炉烟气氧含量控制回路,进一步的研究工作将集中在处理大延迟对象和如何确定标准用以切换控制对象模型的问题上。

