0 引言
积分作用从某种意义上来说是人的记忆功能的模拟。对人而言,记忆功能具有某种选择性;在控制中,人总是有选择地记忆有用的信息而不记忆无用的信息。根据这一发现,周其鉴于1983年提出了著名的仿人智能积分控制算法:

其中:u-控制输出;Kp-比例系数;k-抑制系数;e-误差;e-误差变化率;em,i-误差第i次峰值。
但是,信息的有用性是相对的,当时过境迁时,原来一些有用的信息会变成无用。这时除了不记忆当前无用的信息外还会遗忘那些原来有用而当前变得无用的信息。因此,仿人智能积分控制中的积分作用除表现人的记忆与不记忆两种行为外,还应该加上遗忘行为。
1 仿人智能积分控制
常规PID控制中的积分作用,不加选择地“记忆”了误差及误差变化的所有信息,其中也包含了对控制不利的信息。因此,这种积分作用缺乏智能性,其对误差的积分过程如图1所示,且这种积分作用的针对性不强,甚至有时不符合控制系统的客观需要,只要误差存在就一直进行积分,造成“积分饱和”。
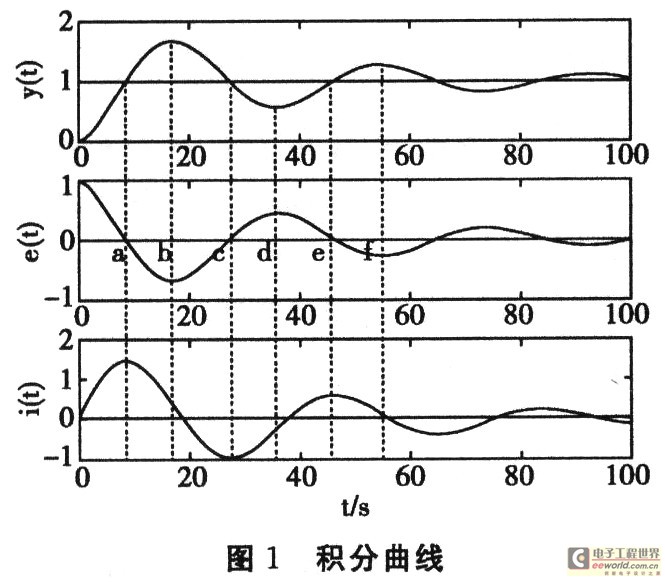
在积分曲线的(c,d)段,积分作用增加一个正量的控制有利减小回调,但在(d,e)区间积分作用继续增强,其结果势必造成系统再次出现超调,这时的I控制作用对系统有害无利。为了克服这种积分控制作用的缺点,满足ee>0,加上积分作用。这样,积分控制作用及时给出合适的附加控制量,能有效地抑制系统误差的增加,而在ee>0时,取消积分作用,使系统借助惯性向稳态过渡。
2 反积分仿人智能控制
从动力学角度来看,系统误差的产生是由能量不平衡而导致系统应有能量损失的一种表现。在系统控制时,比例作用的主要目的是建立系统新的能量平衡,而积分作用的主要目的是弥补系统中应有的能量积累。因此,良好的控制应该预先补充较多的能量尽快地使系统恢复,再在系统恢复的过程中逐步退回一些原来补人太多的能量,避免引起系统超调。为了使积分作用更加合理,在误差增大区间施以较强的积分而在误差减小时则应施以适当的反向积分使多余积分退出。这样,系统在达到新的平衡时保持应有的能量。
实际上,仿人智能积分控制从某种角度来说,不仅具有常规的积分功能,还具有类似于微分的功能,并且,这种用智能积分来体现微分功能的控制既敏感了误差的变化趋势又不像微分那样对噪声也非常敏感。因此,采用仿人智能积分控制时一般不需要再加微分作用。由图2可见,在AB与CD两个区间,反积分仿人智能控制和仿人智能积分控制的积分作用基本相同,主要体现常规积分作用,但在:BC与DE两个区间,只有反积分仿人智能控制的积分与微分的趋势保持一致,因此更好地体现了微分功能。表现在控制方面,则是控制器观察到误差将以某个速度通过误差零点时,将采取拉力的作用方式以防止大的超调量,在相平面内,D控制作用实际就是误差的相轨迹。因此应削弱控制初期D控制的作用;当误差接近0时,则加强其作用,使D控制作用主要在误差较小时起作用。
3 改进仿人智能控制
综合上述分析可知,合理的积分调节系数应该是:
在ee>0区间上,在误差较大时,希望积分增益参数KI不要太大,否则∫edt产生较大的值,响应产生振荡;在误差较小时,希望积分增益增大,以消除系统的稳态误差。期望的积分增益的变化可选取如图2所示的曲线。
据此构造如下非线性函数:
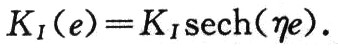
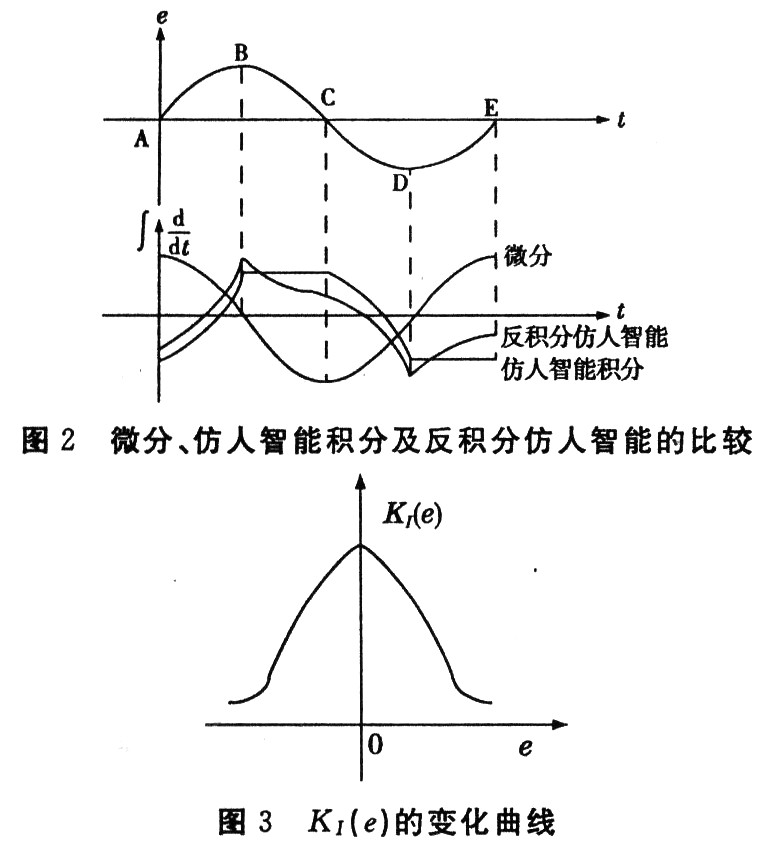
在ee<0区间上,使用仿人智能反向积分作用以使系统的超调减少,此区间反积分调节系数与微分调节规律相似;在误差较大时,反积分系数不要太大,避免减弱P控制作用;在误差较小时,则加强反积分作用。
据此构造如图的构造函数,得到如下改进仿人智能算法:

式中,KI+(e)=KI+sech(αe);KI-(e)=KI-sech(βe);其余参数均同(1),(2)式说明。
4 仿真研究
为了检验所设计系统的控制品质,在单位阶跃输入作用下,对工业工程中普遍存在的二阶加纯滞后对象进行仿真,仿真分别在滞后较小和较大两种情况下进行,并与PID控制器进行比较。下述各图实线为仿人智能控制结果,虚线为PID控制结果。
(1)当滞后较小时:
被控对象传递函数为(采样时间为1秒):

仿人智能控制器参数:Kp=1.3、k=0.8、KI+=0.001、KI-=-0.002、α=1、β=0.7;PID控制器参数为:P=0.2、I=0.15、D=0.2。仿真结果如图4所示。
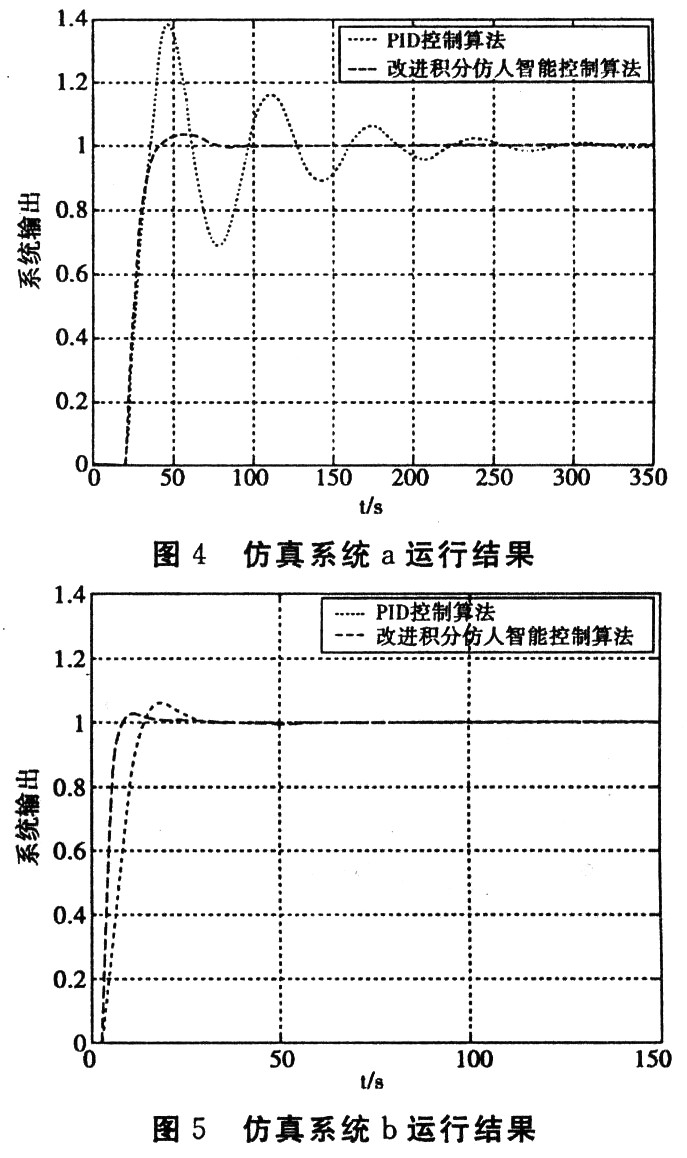
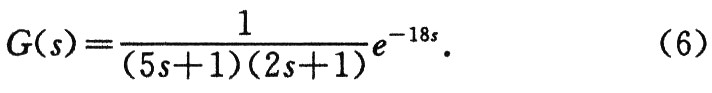
仿人智能控制器参数为:Kp=1.3、k=0.8、KI+=0.6、KI-=-0.02、α=1、β=0.7;PID控制器参数为:P=0.3、I=0.04、D=0.08。仿真结果如图5所示。
5 结束语
本文在仿人智能积分控制算法和反积分仿人智能控制算法的基础上构造了系统的非线性积分系数和实时整定积分系数,通过仿真结果得知:改进的仿人智能控制器对对象参数变化不是很敏感,并且对具有大延迟的对象,不论在稳定性、快速性以及准确性方面都比PID控制具有明显的优越性。而且随着τ/T的增加,即系统的可控性越来越强,改进的仿人智能控制的优越性就越明显。

