在现代战争中，随着精确制导武器的广泛使用，飞行控制技术的研究已日趋深入和普及。空地导弹在飞行过程中因弹道设计的需要一般分为滑翔、点火、转弯、俯冲等多个阶段，而每个阶段均对应几个或多个特征点。根据特征点的不同可把弹道划分为多个时间段，每个时间段对应不同的控制律，所以在相邻时间段的临界点，其控制系数会发生跳变。这将造成计算结果(控制量)在该点的突变，从而影响弹体的稳定飞行。这里论述了某无动力弹的飞行控制系统中解算控制率的方法，以及对其弹道临界点的平滑处理，并用数字信号处理器对其算法进行了工程实现。
2 用PID算法计算控制率
比例积分微分控制器(简称PID)控制简单、可靠，物理意义明显，在工程实践中已广泛采用。PID控制器由比例单元、积分单元和微分单元组成。其输入e(t)与输出u(t)的关系为：
在无动力空地导弹飞行控制过程中，飞行姿态误差信号分别为俯仰角误差θ(t)、偏航角误差ψ(t)和滚转角误差γ(t)。位置误差信号分别为：高度误差日(t)、偏航误差Z(t)和纵向误差X(t)。钻地航弹通过改变俯仰角V1、偏航角V2、滚转角V3来减小姿态误差和位置误差。因此，PID控制的输入为θ(t)，ψ(t)，γ(t)，H(t)，Z(t)，X(t)，输出为V1(t)，V2(t)，V3(t)。根据飞行力学中姿态角误差与位置误差的因果关系，并将PID控制关系式离散化，得到输入与输出的关系为：
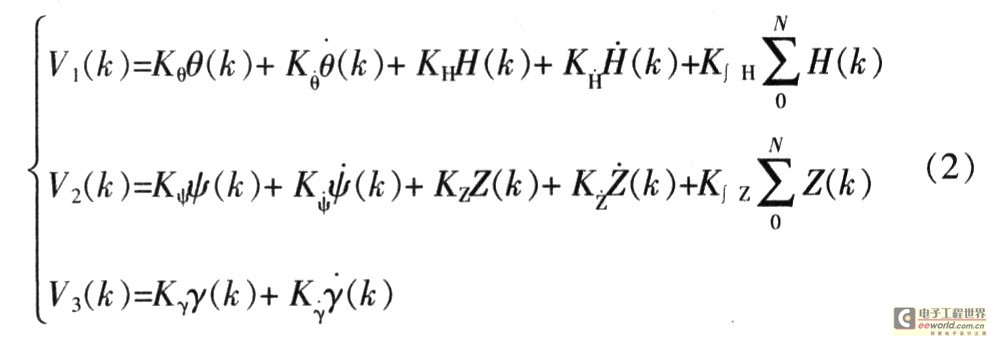
式中：所有K都是经过仿真后得到的各特征点的PID系数。
以上捕述的数学模型又称为位置型PID算法，该算法有很大的局限性，利用该算法容易产生积分项溢出。如果将计算的控制率直接用于控制回路，会造成控制回路的失稳。另外，由于钻地航弹的姿态角与位置的改变滞后于舵机的变化，况且由于受到航弹操纵性的影响，弹道误差也不可能瞬间消除，所以很有可能在较长的一段时间内弹道误差始终为正或为负。图l给出一段时间内的弹道轨迹。
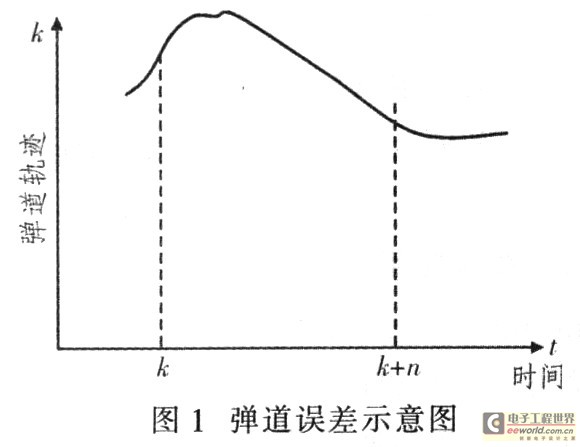
图l中，虚线为方案弹道，实线为真实弹道。在k△t和(k+n)△t时刻，弹道误差为0，在两个时刻间的n个点，真实弹道与方案弹道的差均为正值。此时，积分项
有可能较大，直至溢出。况且计算控制率时只考虑到当前的弹道误差和姿态误差，而没有考虑到前一点的控制率，有可能使得V(k)一V(k一1)比较大，按照该控制率操纵弹的飞行，使得钻地弹飞行时产生剧烈的振荡，影响钻地弹的稳定飞行。所以利用该算法求解控制率时有一定的局限性，现讨论改进型的PID算法一增量性PID算法。
将式(1)离散化可得：
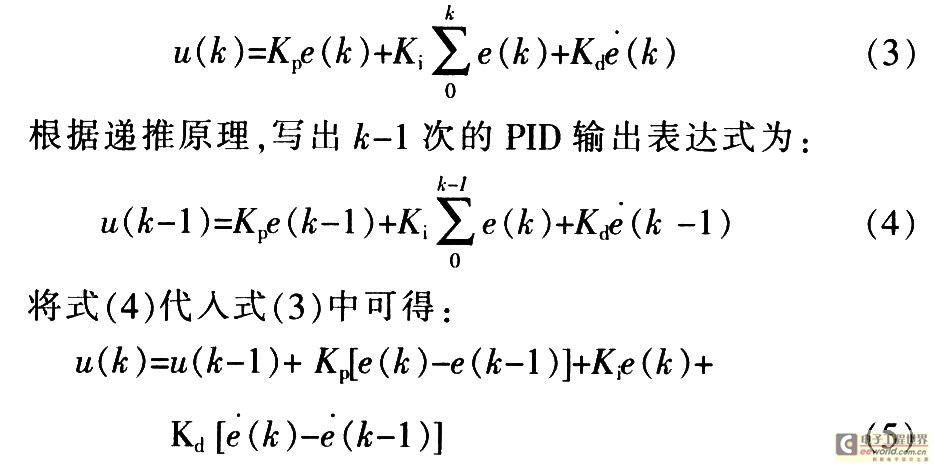
由式(5)可知，当前的输出误差由前一点的输出误差、输入误差和当前的输入误差组成，表明了一个递推关系，所以称为增量性的PID控制。
将式(5)改写成增量性的递推关系．有：
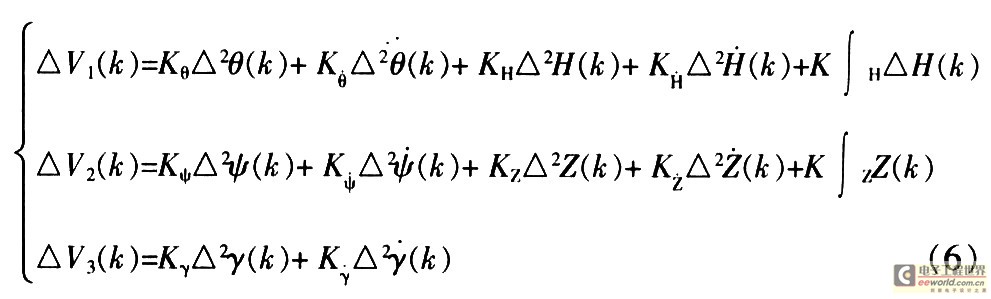
3 临界点的平滑处理
在弹体的飞行过程中，不同飞行段的PID控制系数不同，在不同飞行段，PID系数甚至相差约10倍，所以临界点的控制变量按照式(6)计算时会出现较大的增量，把算出的临界点的控制变量带入舵机控制，会给弹体的稳定飞行带来很大的影响。所以合理处理临界点的控制变量也是保证弹体稳定飞行的一个重要环节。
处理临界点的控制律有2种方法。一是限幅原理，即每次的控制增量不大于5°。这种方法被贯穿在所有点的控制变量解算过程中。该方法原理简单，但仅是粗线条地限制了控制率增量不能过大，不能正确反映控制变量的变化趋势；二是采用加权平均法处理临界点附近的控制变量，使得控制变量曲线比较平滑，而且临界点的控制变量前后具有延续性。避免了产生较大增量影响弹体的稳定飞行。
加权平均法的处理思想是对n项采样结果取不同的权重，然后相加，其具体的计算方法为：
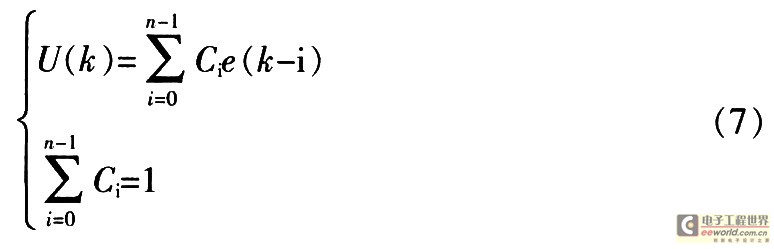
式中：C0，C1，…，Cn-1为各次采样系数，体现了各次采样值在平均值中所占的比例。
一般而言，采样次数愈靠后，取的比例愈大，这样可增加新的采样值在平均值中的比例。该方法可根据需要突出信号的某一部分，抑制信号的另一部分。
在此采用8点加权平均法计算跨临界点的控制变量。如果计算k点的控制变量，则选用8个点的加权系数，即：
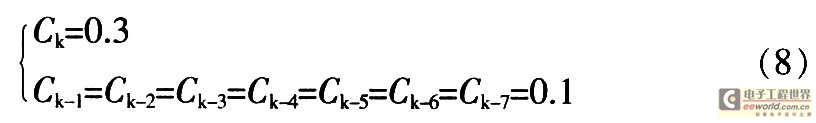
这里，采用加权平均法处理临界点及临界点前7个点的控制变量。从而把临界点突兀的控制增量变为渐缓的控制率增量。
4 系统的工程实现
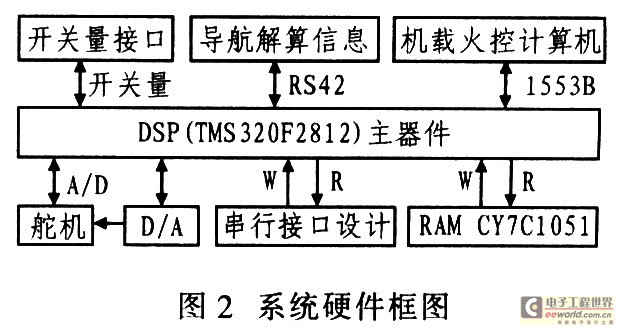
该系统采用TI公司的TMS320F2812作为CPU，用以实现计算、通信、数据存贮、舵机控制等功能。该器件的工作频率为150 MHz，能够在较短的时间内(几十微秒)完成控制变量的计算。图2给出该系统的硬件框图。
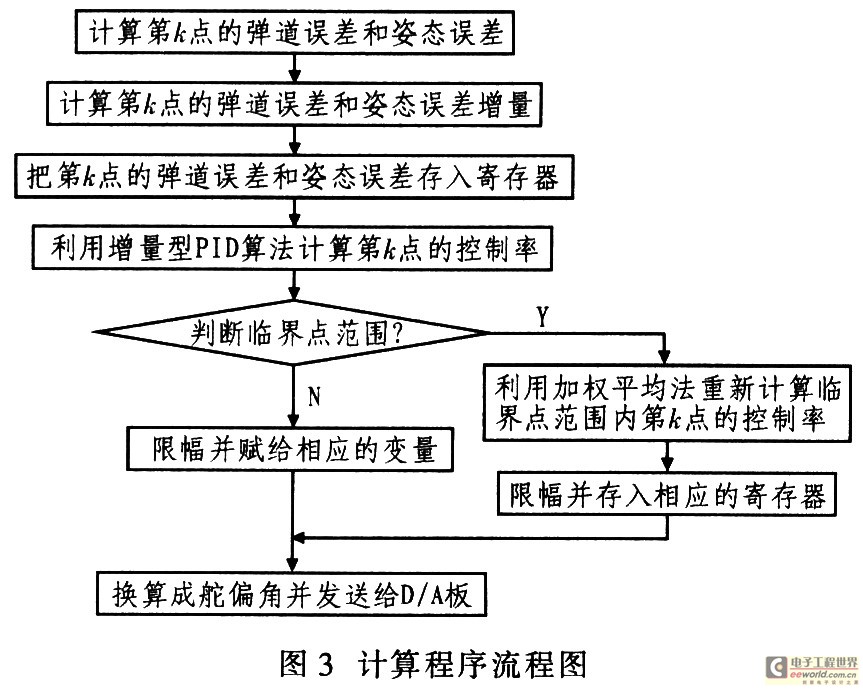
计算程序所要完成的主要工作是计算控制率，并把控制增量转化为舵机的偏转角。根据增量型PID算法和处理临界点的加权平均法计算控制率和舵机偏转角。在实际加权平均法计算中，为了提高速度，借鉴滑动滤波的处理方法，即先在RAM中建立一个数据缓冲区，依顺序存放8个采样数据，每采进一个数据，就将最早采集的那个数据丢掉，而后求含新数据在内的8个数据的加权平均值。这样即可加快数据处理的速度。图3给出其程序流程图。
5 实验及结论
图4给出某次实验中通过增量型PID算法计算出飞行过程中每个点的控制变量曲线。由图4(a)可知，未经平滑的控制变量变化较大，尤其是在临界点上控制变量发生跃变，从而使弹体失控，造成灾难性的后果。图4(b)给出通过限幅和加权平均法进行平滑处理后的控制变量曲线。
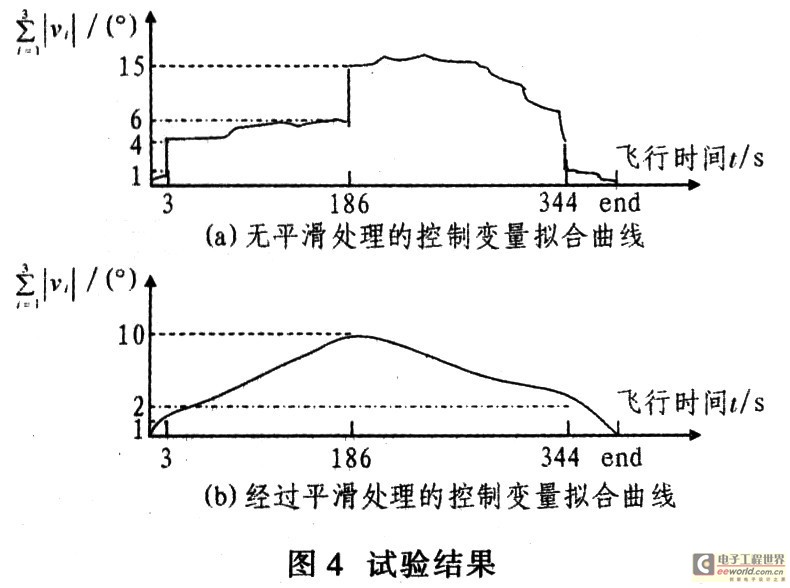
由图4(b)可见，控制变量较为平滑。这样的处理结果，使得弹道上相邻两个点的控制增量较小，即每次弹体飞行调整的姿态角较小，从而使弹体飞行所需的过载较小，保障了无动力弹的稳定飞行。