摘  要： 为IoT系统中的协同中继通信系统提出了一种分批机制的盲信道估计方法和一个包括改进的RCA误差函数的代价函数，并采取IRLS算法解决优化问题。仿真结果表明，该盲信道估计能正确地估计CSI，并且无需任何训练序列，证明了该方法在只依靠小批量矢量的情况下能实现快速盲信道估计的能力。
关键词： 物联网；传感器网络；盲信道估计；协同中继通信；衰落信道；信道状态信息(CSI)

　“物联网”IoT(Internet of Things)指的是将各种信息传感设备(如射频识别(RFID)装置、红外感应器、全球定位系统、激光扫描器等)与互联网结合起来而形成的一个巨大网络[1]。其目的是让所有的物品都与网络连接在一起，系统可以自动和实时地对物体进行识别、定位、追踪、监控并触发相应事件。物联网已被用于许多领域，例如零售、电子保健、医药、能源、农业和环境。物联网是一场依靠许多重要领域里动态创新的技术革命，随着集成电路的微型化和纳米技术的不断进步，越来越小的物体将有能力被集成在RFID的标签里。
　RFID标签是一个集成了众多传感器的装置，从对物联网的定义来看，其可以被当作由很多RFID组成的特别的传感器网络系统。传统的分布式RFID标签由于受到能源、物理尺寸和电池操作的限制，对其进行更换将会很不经济或很困难[2]，而目前的技术又不足以处理对未来能源应用局限性的问题。因此，在设计制造大规模、低成本的传感器网络时，满足能源效率[3]是很重要的一点。任何有关这方面的改善都将是一个重要的收益，在大多数情况下，能量传输过程中最容易产生能源消耗。一种有效的解决方案是采用双天线阵列的信道衰落，这种方法在蜂窝和无线局域网(WLAN)中得到了广泛应用，并提供了以前无法想象的数据传输速率和可靠的传输性能[4]。然而，物联网标签(在本文的介绍中称之为“节点”)通常只有一个天线，这就必须利用节点的协同通信来解决这个问题，节点的协同通信允许实现使用了分布式节点的虚拟双天线阵列[5-6]。目前绝大多数文章在分析他们的方法时是基于信道状态信息CSI(Channel State Information)完全或部分已知的假设。
通常来说，最好的中继是根据包含了一跳和二跳信道信息的CSI来选择的。在选择最好的中继节点时具有部分CSI的性能是必需的，并且额外的中继点无法对增加性能做出贡献。
在物联网系统中，RFID标签经常放在可移动的物体上(如商品、汽车和宠物)。由于节点的机动性和传播环境的影响，存在大量的时间变化。此外，在满足未来物联网系统中高速数据率服务的要求中存在的主要障碍之一是多径传播引起的信号衰落。
　基于物联网系统特性的考虑，引进协同中继通信至物联网系统中，从而通过分集增益来节省能源和增加网络寿命，本文为物联网系统的协同中继通信系统提出了一种分批机制的盲信道估计的方法和一个代价函数，该函数包括改进的RCA的误差函数，并采取IRLS算法解决优化问题。仿真结果表明，该盲信道估计能正确地估CSI，并且无需任何训练序列，证明了该方法在只依靠小批量矢量的情况下实现快速盲信道估计的能力。
1 协同中继通信系统模型
　根据物联网系统要求所建立的协同中继系统如图1所示，包括一个信息源S、中继R和目标D节点，这些都只具有一个天线。尽管看上去简单，但是系统存在许多有待解决的协同通信方面的理论问题，并且可以通过多中继点扩展到更加复杂的中继网络。假定S和R利用多路径通道进行协同传输，并且假定CSI不能在传输节点(如S和R)中得到，在接收端CSI的获取取决于信道的衰减速度。

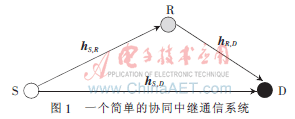
　系统模型基于如下假定：
　假定A：传输的信息符号序列和相应的信道噪声为等差序列。
　假定B：传输的信息符号序列和相应的信道噪声是独立的序列。
　假定C：传输的信息符号序列满足次高斯和零均值分布。
　以s(k)表示从S和Mi，j传输的信息符号序列，(i，j)∈{(S，R)，(S，D)，(R，D)}为相应的信道记忆长度。在第一阶段，分别以xS，R(k)和xS，D(k)表示在R和D处在时间段k中接收到的基带信号[7]。

其中惩罚因子c是一个正标量，以N表示信号长度，可得到：

3 仿真结果
　采用了所提出的盲信道估计方法，并使用瑞利和Nakagami分布进行仿真。Nakagami分布可归纳为瑞利分布，但在衰减的程度上有更多的控制。在信号传输节点上(如S和R)使用了滚降系数α=0.5的平方根升余弦传输滤波器。不失一般性，本文只显示了传输滤波器联合信道实部和节点间信道的仿真结果。在所有的仿真中，设置信号噪音比Eb/N0=10 dB，批向量大小N=200，并且采用了16-QAM方案。
3.1 放大转发协作通信
　在放大转发协作通信的情况下，中继节点R接收到一个从源节点S传送的嘈杂的信号。该嘈杂的信号只是简单地被放大和转发到目标节点D[12]。比较通过这种方法实现的盲信道估计性能，确立信道hS，D、hS，R和hR，D的顺序，分别为10、15和20。在这些仿真中，由30个蒙特卡罗线索数来描绘这些图表。真正信道和预测信道的结果分布分别如图2、图3、图4所示。通过这三幅图可以观测以下结果：(1)这种方法对不同顺序的衰减信道有较好的鲁棒性；(2)盲信道估计性能即使是在小批量矢量大小的情况下也是令人满意的。

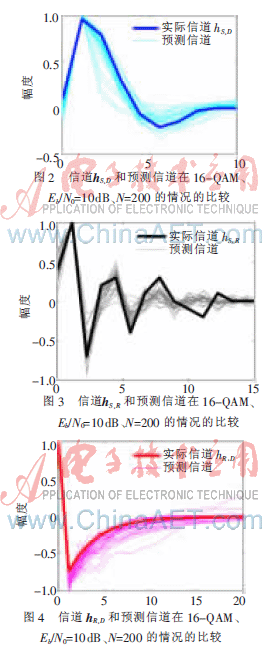
　此外，这些仿真的算法迭代次数大约为50，并且预测的性能在增量为Eb/N0或N的情况下会更好。

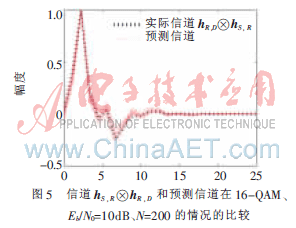
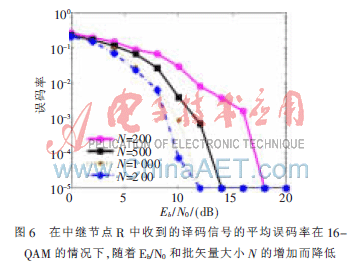
　图6为在中继节点R中收到的译码信号的平均误码率。蒙特卡罗线索数目为500。结果表明，盲信道估计性能在增量为Eb/N0或N的情况下得到提高。其中噪音是客观因素，无法通过努力而改变，但可以扩大批矢量的大小N，然而这意味着操作的负担将变重。但这种方法可以通过很小的批矢量大小得到满意的预估性能。此外，还可以看到，图6中N=1 000和N=200的曲线非常接近，意味着我们不要使用N≥1 000的太大的批矢量通过增加操作量来提升性能。

　本文为物联网系统中的协同中继通信提出了一种盲信道估计方法。阐述了包括用于改进的RCA代价函数的误差项的一个优化问题，并采用IRLS算法来解决该优化问题。通过这种方法，可以得到正确的CSI，并用它来选择最佳的中继节点和波束成型。仿真结果表明，该盲信道估计方法在只需很小的批矢量大小的情况下能正确地估计信道。更多没有在本文中出现的仿真结果也同样显示出该方法对于实现快速盲信道估计的能力。
参考文献
[1] Internet of things in 2020： roadmap for the future. http://www. smart-systems-integration. org/public/internet-of-things， 2008.
[2] GOLDSMITH A J， WICKER S B. Design challenges for energy constrained ad-hoc wireless networks[J]. IEEE Trans actions on. Wireless Communications， 2002，9(4)：8-27.
[3] Early challenges regarding the “Internet of Things”， http://ec. europa. eu/yourvoice/ipm/forms/dispatch?form=IOTconsultation， Nov. 2008.
[4] CALDERBANK R， PAULRAJ A， POOR H V， et al. MIMO wireless communication[M]. Cambridge， U.K.: Cambridge Univ. Press， 2007.
[5] SENDONARIS A， ERKIP E， AAZHANG B. User cooperation diversity. Part II. Implementation aspects and performance analysis[J]. IEEE Transaction on Communications， Nov. 2003， 51(11)：1939-1948.
[6] CUI Shuguang， GOLDSMITH A J， BAHAI A. Energy-efficiency of MIMO and cooperative MIMO techniques in sensor networks[J]. IEEE Journal on Selected Areas in Communications， 2004，22(6)：1089-1098.
[7] LI H， ZHAO Q. Distributed modulation for cooperative wireless communications： A description of four schemes[J]. IEEE Signal Processing Magazine， 2006，23：30-36.
[8] YANG J， WERNER J J， GUY A. The multimodulus blind equalization and its generalazed algorithms[J]. IEEE Transactions Journal on Selected Areas in Communications， 2002，20(5)：997-1015.
[9] L AZARO M，  SANTAMAR A I， V A J， et al. Blind equalization using the IRWLS formulation of the support vector machine[J]. Signal Processing， 2009(89)：1436-1445.
[10] ERDOGAN A T. A fractionally spaced blind equalization algorithm with global convergence[J]. Signal Processing， 2008(1)：200-209.
[11] SAYED A H. Fundamentals of adaptive filtering[M]. New York： John Wiley & Sons， 2003.