1理论基础

　　1．1正交双通道取包络

　　为了方便处理，在此假设待处理的信号都是正交双通道的，如果输入信号不是正交双通道信号，那么可以通过如下处理来获得正交双通道信号。假设输入信号的表达式如下

　　通过三角公式的积化和差可得

　　同样可以用平方求和法来取包络。

　　1．2信道设置

　　信道设置，共有两种类型的信道模型，这里信道都是正频域信道。一种是16通道，另一种是32通道；信道总带宽均为200MHz(-100～100MHz)。当通道数是16时，第1通道的低通滤波器通道带宽设置为-3．125～3．125MHz，该通道右过渡带为3．125～3．5MHz，这样每个相邻通道有一定的交叠，交叠区的带宽为0．375MHz；第1通道的中心频率为6．25MHz，通带是6．25MHz，有两个过渡带，左过渡带与第1通道的右过渡带重叠。以此类推，中心频率以6．25MHz递增，通带宽度为恒定6．25MHz，每一个通道有两个过渡带，左过渡带与前一个通道的右过渡带重叠。当通道数是32时，第1通道的带宽为-1．5625～1．5625MHz，该通道的右过渡带为1．5625～1．75MHz，交叠区带宽为0．1875MHz；第2通道的中心频率为3．125MHz，有两个过渡带，左过渡带与第1通道的右过渡带重叠。以此类推，中心频率以3．125MHz递增，通带宽度为一恒定值3．125MHz，每一个通道有两个过渡带，左过渡带与前一个通道的右过渡带重叠。图1和图2为16通道和32通道的频域图。

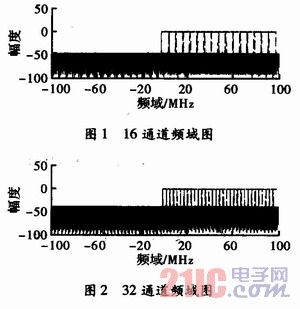
　　1．3输入信号形式

　　调频信号带宽恒定为80MHz，起始频率为5MHz，截止频率为85MHz。调频方式分成3种：线性调频、三角调频和正弦调频。调频信号的通用公式如式(10)和式(11)所示。

　　式中，A表示信号的幅度；KFM表示调频参数；具体值需要根据具体信号计算；s(τ)表示调谐方式函数。

　　2测试流程

　　根据分析，在16通道中，第1通道与第16通道没有信号输出。第2通道与第15通道有部分信号输出，第3通道到第14通道都被信号完全覆盖；在32通道中，第1，2，35和36通道没有信号输出，第3和34通道有部分信号输出，其他通道都被信号完全覆盖。在实际设计中，如果该通道有信号就默认为该通道频域完全被覆盖。但实际情况中却不是这样的，有些通道只有部分信号，输出的包络就比较小，这样就会导致出现异常值。

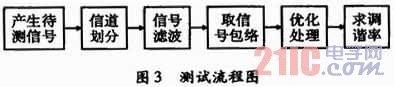
　　测试过程分成6步：产生待测信号、信道划分、信号滤波、求取信号包络、优化处理，求调谐率，其中，优化处理是指剔除极大值和极小值，这时剔除应该有个范围，而不是一个简单的极值，在这里波动范围设为极值的1％。求调谐率用的方法是用公式μ=B／τ，式中，τ是包络的脉宽；B是单个通道的带宽。如果信号在该通道内覆盖很小，那么用包络取出的τ很小，进而会影响调谐率的测量。最好的办法就是将改异常的μ值剔除，剔除的时候会存在这样的问题，如果在两个边界通道中信号覆盖度相差太远，即使有优化处理，输出必然还会有一个歧义值。上述方式求出的只是μ的绝对值，可以通过通道信号输出前后来判断正负，如果fnow>fbe，μ为正；否则μ为负。

　　3测试结果与分析

　　3．1线性调频信号测试

　　线性调频信号的脉宽为16ms，由此可知，调谐系数KFM为5×109。图4为16和32通道的测试结果。

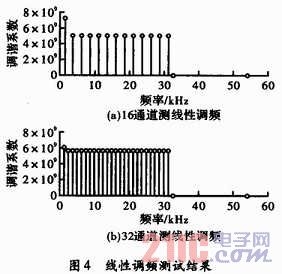
　　从图4中两个信道测得的调谐率可以判断出调谐方式是线性调频。将16和32通道的输出进行比较，可以看出32通道的输出更加光滑。在16通道下测得的线性调谐系数为5．05×109；在32通道下测得线性调频的调谐系数为5．65×109；计算可得，32通道的调谐率误差约为13％，16通道的误差约为1％。

　　3．2三角调频信号测试

　　三角调频信号脉宽为16ms，由此可知，调谐系数KFM为1×1010。图5为16和32通道的测试结果。从图5两个信道测得的调谐率可以判断出调谐方式是三角调频。将16和32通道的输出进行比较，可以看出32通道的输出更加光滑。16通道时测得的调谐系数是1．04×1010，32通道时测的调谐系数为1．15×1010；16通道调谐率测量误差约为4％，32通道调谐率测量误差约为15％。

　　3．3正弦调频信号

　　正弦调频脉宽为8ms，调谐系数KFM为40×106。图6为16和32通道的测试结果。

　　根据测试得到的调谐率可以看成是对一个正弦函数进行求导所得。将16和32通道的输出进行比较，可以看出32通道的输出更加光滑。此时16通道的正弦调谐系数为46×106，32通道的正弦调谐系数为50×106，通过计算可以得到16通道测正弦调频的测量误差约为15％，32通道时正弦调频的测量误差约为25％。

　　4结束语

　　在同一种调频方式下的信号，通过通道个数不同的信道，调谐率测量误差不同，在通道个数越多的情况下测量误差越大，上述3组测量结果可以说明这个问题。这种情况下的误差主要由τ产生，即τ是受到调谐方式的影响。在不同形式的调频信号在相同的信道化条件下，正弦调频的调谐率测量误差最大，线性调频的测量误差最小；这也进一步说明调谐率的测量误差受调谐方式的影响。通道数越多输出越平滑，越容易判断出调谐方式。总之，通道数过多影响调谐系数的测量，通道数过少对调谐方式的判断会存在影响。