模糊控制比例因子与空调系统稳定性关系的研究
2009-02-23
作者:王沣浩 俞炳丰
摘 要: 介绍了两输入、单输出的模糊控制系统的仿真,讨论了比例因子(Ke、Kec、Ku)对系统响应的影响,着重研究了比例因子与系统稳定性之间的关系,并在此基础上提出了空调系统比例因子的设计原则。
关键词: 空气调节器 模糊控制 比例因子 稳定性
模糊逻辑控制(FLC)是近年来控制学术界一个引人注目的研究领域,并且已经成功地应用在空调系统中[1][2]。实践证明,与传统控制方法相比,FLC对环境干扰、过程参数变化等具有较强的鲁棒性,并能抑制非线性因素对控制器的影响[3]。但是FLC也有自身的缺陷,如FLC的稳定性问题等,而且FLC对严重影响控制器动、静态品质和控制的鲁棒性的比例因子Scaling Factors(简记为SF)也缺少系统的理论。事实上,FLC中SF的选择标准一直就是一个公认的难题[4]。
本文中所涉及的参量符号及具体含义如下:
c(nT):模糊控制器的输出控制量
e:实际温度偏差
ec:实际温度偏差的变化
E(nT):模糊控制器的温差输入量
EC(nT):模糊控制器的温差变化输入量
Ke:温差变量的比例因子
Kec:温差变化变量的比例因子
Ku:输出控制量的比例因子
Yu:输出控制量的基本论域
l:输出控制量的论域
m:温差变量的基本论域
n:温差变化的基本论域
T:采样时间间隔
U(nT):控制器的实际输出控制量
Xe:温差变量的论域
Xec:温差变化变量的论域
Y(nT):系统的响应
1 SF与空调器模糊控制系统响应之间的关系
在FLC系统中,当由计算机实现模糊控制算法、进行模糊控制时,每次采样得到的被控制量需经计算机计算,得出FLC的输入变量误差及误差变化。为了进行模糊化处理,必须将输入变量从基本论域转换到相应的模糊集的论域,即将输入变量乘以相应的比例因子,一般用Ke、Kec表示。而每次由模糊控制算法计算出的控制量,还不能直接用来控制对象,须乘以输出量的比例因子(常用Ku表示),将其转换为被控制对象所能接受的基本论域中的量,即:Ke=n/Xe;Kec=m/Xec;Ku=Yu/l。
图1为一个两输入、单输出的空调器模糊控制系统框图,由该图可以得出下述关系式:
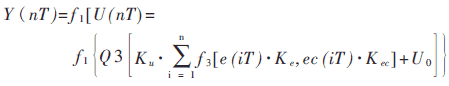
由上式可以看出,系统nT时刻的响应,既取决于e(iT)和ec(iT),又取决于Ke、Kec和Ku的大小,显然改变系统的SF就能改变系统的响应。研究表明:增大Ke可以有效地减小系统响应的稳态误差,但是Ke过大会引起系统的超调并降低系统的收敛速度;增大Kec值一方面加快了系统的响应速度,另一方面也使系统超调次数明显增加;而Ku的变化是对FLC控制查询表的修正,其值不仅影响误差变量e的覆盖域,也影响误差变化ec的覆盖域。在保证Ke和Kec不变的条件下,增大Ku值一方面可以减少系统的动态响应过程的时间,另一方面会引起较大的超调,并产生振荡。在实际的控制中,可以通过调整Ku值来改善系统的控制效果,即:在被控对象时间常数较长时,采用较大的Ku值以减少系统的动态响应时间;被控对象时间常数较小时,采用较小的Ku值以防止系统产生振荡。关于SF对空调器模糊控制系统响应的详细分析可参见文献[5]。
应该注意的是SF的选择并不是唯一的,也就是说几组不同的SF值可能产生同一种响应效果。为此本文将进一步研究SF与空调系统稳定性之间的关系。
2 SF和空调器模糊控制系统稳定性之间的关系
一个理想的模糊控制器首先应保证空调器的控制系统满足稳定性的临界条件,因此研究SF与系统稳定性的关系有着重要的意义。
2.1 Kec和空调系统稳定性之间的关系
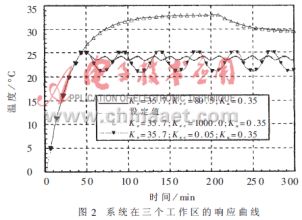
在大量的仿真基础上,作者发现在0<Kec<+∞ 范围内,可以将Kec对系统响应的作用分为三个区域,即超调区、工作区和非稳定区,其代表的响应曲线如图2所示。具体如下:
超调区:0<Kec≤C1,C1为常数;
工作区:C1<Kec≤C2,C2为常数;
非稳定区:C2<Kec<∞。
在超调区由于Kec的值较小,相当于控制器对误差变化有较大的控制区域,而实际的误差变化ec则远小于这个区域,因此在该区域中控制器仅依靠误差来调整控制器的输出,而忽略了误差变化对控制器的作用,造成了较大的超调,如图中Kec=0.05对应的曲线所示;当Kec值增加到大于某个常数后,系统进入非稳态区。和超调区正好相反,由于Kec值较大,系统对误差变化的覆盖域较小,而实际的ec值则远大于这个区域,因此系统长时间处于EC=±N的工作状态,虽然增强了对误差变化的控制,但是由于其忽略了误差变量对控制器的作用,系统变得非常敏感而难以稳定,如图中Kec=1000.0对应的曲线所示。设计FLC时应使Kec位于正常的工作区,从而取得较好的控制效果。因此如何确定常数C1和C2值的大小就成为问题的关键。
确定常数C1和C2,应以保证系统对误差变化的覆盖域接近于实际控制中ec的变化范围作为基本出发点,最大限度地发挥出所有控制规则的作用。这里我们取误差e在稳定区域的变化范围为:
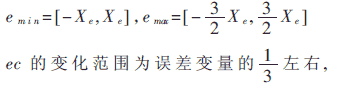
即:
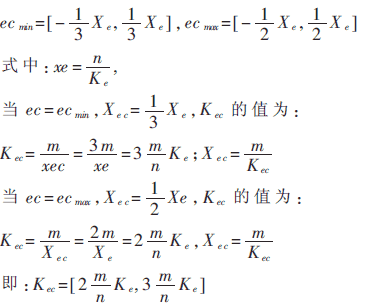
表1是某空调系统在不同Ke条件下Kec的正常工作区范围。

2.2 Ke、Ku与系统稳定性的关系
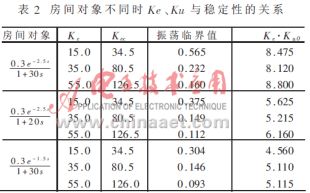
为了进一步研究Ke、Ku与稳定性的关系,分别在三种不同的房间对象下取Kec=2.3Ke,并逐渐增大Ku值直到系统输出振荡,Ku的临界振荡值Ku0如表2所示。
从表2可以得出:在房间温度控制对象参数不变的条件下,系统输出的临界振荡参数Ku0与Ke的乘积约等于一常数C。当Ke·Ku<C时系统不会发生振荡;当Ke·Ku≥C时系统输出不稳定。
3 空调系统模糊控制比例因子设计原则
本文提出SF的设计原则如下:
(1)根据控制参数的精度要求确定误差e的比例因子Ke的大小,保证误差的控制死区小于允许的控制误差范围,即:Ke≥ ,δ为控制参数的最大允许误差。
,δ为控制参数的最大允许误差。
(2)Kec的选择应保证其处于正常工作区范围内。
(3)在保证系统稳定的前提下(即Ke与Ku的乘积
小于系统输出振荡的临界常数),尽可能地增大Ku值
以取得较快的响应速度。
最后,我们得到以下结论:
(1) Kec存在三个响应区域,即超调区、工作区和非稳区。选择Kec时应保证其处于正常工作区范围,
满足式![]() 。
。
(2)在其它参数不变的条件下,系统的临界振荡参数Ku0值与Ke的乘积约为一常数C,当Ke和Ku的乘积小于C时系统会稳定的运行。
(3)本文提出的比例因子设计原则,是在大量的仿真研究基础上提出的,更严格的理论证明还有待进一步研究。
参考文献
1 俞炳丰.柜式空调器模糊控制系统的研制.流体机械,1997(5)
2 Seydou Ouattara. Towards a Methodology for Selecting Good Scaling Factors for a Fuzzy Controller.Fuzzy Sets and Systems,1996;1(83)
3 王沣浩.变频空调器控制系统的仿真研究.流体机械,1998(3)
4 赵 捧.模糊控制器比例因子自整定专家系统.模式识别与人工智能,1996(2)
5 Sinn-Cheng Lin.Design of Self-learning Fuzzy Sliding Mode Controllers Based on Genetic Algorithms.Fuzzy Setsand Systems,1997;1(86)