摘  要： 开发了一种统一的可靠性模型，该模型对系统的硬件失效、软件失效和软硬件交互失效都可以作出解释。硬软件失效可以由熟知的建模方法来解决。而提出了一套利用马尔可夫过程来捕获硬软件交互失效的建模方法论，通过将其应用到真实的通信系统来说明该硬软件混合的建模方法。
关键词： 可靠性建模；软件失效；硬件失效；软硬件交互失效

　针对硬件可靠性和软件可靠性研究领域虽然有着大量的文献，但多数都只局限于单独的硬件或者软件子系统的研究。少数研究者设法为整个系统建立一个混合的可靠性模型，既包括硬件也包括软件。但他们通常认为硬件和软件子系统是相互独立的。
事实上，在许多现代计算机系统内，硬件和软件间的影响很大。例如，参考文献[1]对斯坦福大学的MVS/SP操作系统进行的软件错误分析发现，将近35%的软件错误是和硬件有关的。在这些系统中，硬件和软件子系统不是相互独立的，系统的可靠性受软硬件交互作用的影响。硬件和软件系统之间的交互作用表现在两个方面：积极的和消极的。参考文献[1]中提到的哈勃望远镜机械上的问题，经软件变更而得到了缓和。这意味着通过软件可以修正硬件问题，这就是软件所起的积极作用。另一方面，预料不到的硬件失效模型致使软件在一个非典型的操作模型下执行，而软件因没有被严格的测试过，结果导致系统的性能下降。在失效状态下，操作会更不可靠。

　(5)硬件部件的失效率为λ1。
　(6)局部硬件失效能以概率P1被检测到，一旦检测到，就可通过软件方法以概率P2得到恢复。虽然软件方法及相关的硬件可能找不到退化处，但是也不会有不正确的保护。
　(7)一个检测不到的硬件退化可能会导致硬软件交互失效(失效率为λ3)，检测到的硬件退化可导致执行中止(失效率为λ4)。
　(8)一旦局部硬件失效被检测到，失效的硬件部件就被修正或者是替换，通过软件恢复的概率为μ1a，没有通过软件恢复的概率为μ1b。
　如果退化被检测到却没有通过软件的方法恢复，局部硬件失效可能进一步以概率λ2a演变为总体失效；如果退化被检测到并且通过软件的方法恢复，则以概率λ2b演变为总体失效；如果退化没有被检测到，则以概率为λ2c演变为总体失效。
1.2 模型
　基于(1)和(4)的假设，整个系统的可靠度为：
　Rc(t)=Pr{t时刻无总体失效}×Pr{t时刻无纯软件失效}×
　 Pr{t时刻无硬软件交互的失效}=RHW(t)RSW(t)RHW/SW(t)(1)
　式中，RHW(t)和RSW(t)是纯硬件可靠性函数，纯软件可靠性函数由假设(2)和(3)分别决定的，而软硬件交互失效可靠性函数RHW/SW(t)来自于假设(5)~(9)。
　图1是HW/SW失效模型的状态转移图。

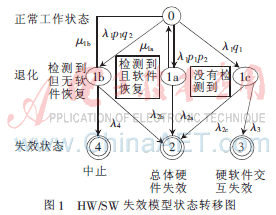
　下面通过其在通信系统中的应用来阐明硬软件混合模型方法。
2 电信应用
2.1 系统描述
　通过将模型应用到无线BSS的一个特殊部件来说明。这个特殊部件是服务器，它是BSc的一部分。服务器按N+1组配置的，组操作在负载均衡的环境下进行的。当一个服务器失效，组中剩下的服务器接管它所执行的任务。每个服务器上运行的故障恢复软件负责管理恢复进程。
　表1列出占用时间和失效数据。表中所示的6个月中的每个月，总计硬件的占用时间的系统日期，不管硬件运行的是软件R1(2列)还是R2(4列)，都已给出。第3和5列是服务器的应用编号，是通过把总的占用时间按每月的天数划分而得到的。硬件设计也是一样，不考虑它执行的是哪个软件，第6列表明了每月来自所有的服务器总的硬件失效的数目。第7列说明了服务器只运行软件R2时的软件失效数。

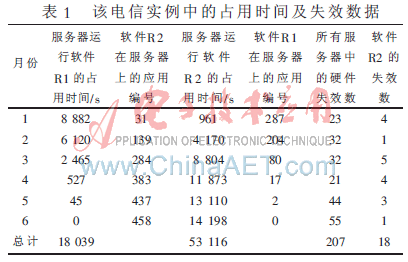
　当区域中有软件失效时，用户会通知技术支持人员，由技术员创建故障列表。如果故障的性质被诊断是程序上的错误，通常会关闭故障列表，而当前的软件释放令不改变。如果故障已经确定与软件失效有关，则要为故障分配安全级别。区域中首次高安全性级别故障的发生与软件更新之间的间隔通常不会超过两周。如果域中有异常多点故障，有关这个重复事件的列表被认为是源故障列表的再现。在绘制表1时，只有源故障列表对高安全性级别的故障有反映。
　表1没有对硬软件交互失效做出详尽的说明。分析故障列表的根本原因时，没有对其进行硬软件交互失效的分类。多数情况下，域中发生的硬软件交互失效都被划分为了硬件失效，因为失效中的硬件因素在故障列表被创建时比软件因素更明显。下面，在调查硬软件交互失效的影响时，在不确定的假设条件下分析硬件失效实际为硬软件交互失效的概率F有多大。
2.2 配置模型
　为了安装硬软件交互失效模型，只关注运行R2的服务器，因为硬软件交互失效模型包含软件失效率λ3，这个参数依赖于软件排错。由于这个实例中系统没有内置的检测硬件退化的机制，在表1中，令P1=0。另外，为了满足λ3>>λ2c，则进行进一步简化，令λ2c=0，则由式(2)可以导出：




　许多现有的可靠性模型都没有考虑硬软件子系统的交互失效，而只考虑了纯硬件和纯软件失效。结果，大多数失效数据都是就纯硬件和纯软件失效而得到的。当建立纯硬件或纯软件模型时，硬软件交互失效被忽略。这对于可靠性预测方法是非常不利的。本文方法由于考虑了硬软件交互失效对整个系统的影响，这样建立的模型比传统的只分别考虑软件和硬件所建立的模型具有更准确的可靠性预测。
参考文献
[1] BAIN L J. Statistical analysis of reliability and life-testing models[M]. New York： Marcel Dekker， 1978.
[2] FRIEDMAN M A， TRAN P. Reliability techniques for combined hardware/software systems[C]. Proceedings of Annual Reliability and Maintainability Symposium， 1992：290-293.
[3] GOEL A L， OKUMOTO K. A Markovian model for reliability and other performance measures of software systems[C]. Proceedings of the National Computer Conference， 1979： 769-774.
[4] HECHT H， HECHT M. Software reliability in the system context[J]. IEEE Transactions on Software Engineering， January， 1986， 12(1)：51-58.
[5] IYER R K. Hardware-related software errors： measurement and analysis[J]. IEEE Transactions on Software Engineering，  February， 1985，11(2)：223-230.
[6] PARZEN E. Stochastic processes[M]. San Francisco， CA： Holden-Day， 1962.
[7] PHAM H， Software reliability[M]. New York： Springer， 2000.
[8] WELKE S R， JOHNSON B W， AYLOR J H. Reliability modeling ofhardware/software systems[J]. IEEE Transactions on Reliability， September， 1995， 44(3)：413-418.