摘  要: 电子式电动机保护装置的种类和现状,指出了电子阻容式保护装置存在的反时限动作特性的弊端,提出了一种利用稳压管PN结的反向指数型伏安特性对阻容式保护器进行反时限特性改善的新方法,使之成为接近理想保护特性的通用型电动机保护装置。 

　　关键词: 电子式  保护装置  反时限特性  电动机 

　　近年来我国电子式电动机保护器已有了一定的发展,越来越多的用户开始尝试选用电子式热保护器来取代传统的以发热、变形带动机构动作为原理的双金属片式热继电器。与传统的热继电器相比,电子式热保护器具有高精度、高可靠性等优点。目前,电子式保护器虽然品种繁多,但归纳起来基本分为以下两种。 

　　(1)单片机式 

　　这种保护器首先建立了与电动机热特性相一致的数学模型,以便对电动机进行热动态跟踪;同时可方便地设计成多功能,充分发挥计算机软件的优势,适用于中大型电动机的综合保护。 

　　(2)阻容式 

　　这类保护器机芯采用模拟电子电路,以简单、价廉、精小、可靠和使用方便而见长。 

　　单就电动机热保护器而言,它无疑具有广阔的市场前景。而一个合格的热保护器必须解决两个关键问题,一是要有高精度的传感器,将表征电动机过载的量检测出来;二是动作特性(即反时限特性)必须与实际的电动机热特性相对应或与标准相近。 

　　以上两种热保护器各有优点,单片机式自然性能良好,但价格贵一些,且不适合对中小型通用电动机保护;而阻容式虽然价格便宜,但保护性能不尽如人意。如果能将阻容式的保护器加以改进,令其保护性能尽量接近标准规定的指标,无疑会给电子式热保护装置的推广使用带来可喜的前景。 

1 电动机保护器过载(或缺相)的动作特性 

1.1 标准动作特性 

　　根据电动机热特性及绕组耐过热能力,电动机过载断相保护的性能指标如表1所示(I_e代表电动机额定电流)。 

　　按国际标准JB3905的描述,电动机的温升与电流的平方成正比。因此给出了反时限的动作时间数学模型: 

    t=τln{I²/[I²-(kI_e)²]}=τln{1/[1-(kI_e/I)²]} 

    式中,τ为阻容电路的时间常数,k为临界动作时的电流过载倍数(过载判据),这里取k=1.1。若规定6倍过载时冷态动作时间为7秒,则推算出动作时间常数为: 

    τ=t/ln{1/[1-(kI_e/I)²]}=7/ln{1/[1-(1.1/6)²]}=204.7s 

　　这样,相应各过载倍数的动作时间(I²规律的动作时间)如表2所示。表2中没有规定2～6倍过载时的动作时间,是因为电动机在2倍过载之后,转差率大增,开始进入T-S特性的非稳定区而迅速堵转,因此2～6倍开区间的动作时间无需规定。 

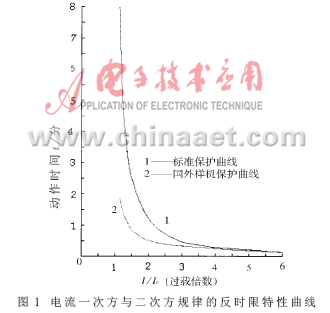
　　I²规律反时限保护特性曲线如图1中曲线1所示。这一保护特性正是电子式热继电器所追求的,不论是单片机式的还是阻容式的均以此作为目标。对于单片机式保护器而言,实现这一目标很容易;而对于阻容式的保护器,要实现这一保护规律却并非易事。 

1.2 电流一次方规律的保护特性(J7T) 

　　二十世纪90年代进入我国市场的电子式热继电器(阻容式)是按电流一次方规律实施热保护的(如日本OMROW的J7T型),之所以没有在阻容电路前增加乘法器电路,是普遍考虑了保护装置的体积、精度及可靠性等问题。作为对比,下面列出按电流一次方规律动作的时间表达式: 

    t=τ/ln[1/(1-kI_e/I)] 

　　仍取k=1.1,而6倍过载保护动作时间取7秒,则其动作时间常数应为τ=34.1s。相应各过载倍数下保护动作时间(一次方规律的动作时间)见表2。电流一次方规律的动作时间及特性曲线仅在高过载倍数(大于等于3.5)下与标准相近,而低过载倍数下两者均与标准相去甚远。1.15倍过载时,动作时间只有1分49秒,出现了过保护,虽然满足了开区间<1h的动作要求,但却大大限制了电动机固有过载能力的利用,这种过保护也是一种不成功的保护。 

2 改进的阻容式保护器反时限特性 

　　本文所追求的是既要标准的保护特性,又要保护装置的低成本,因此希望对阻容式保护特性加以改进。如前所述,电动机过载时温升与电流平方成正比,这样低过载倍数时动作时间应长一些,以便充分发挥电动机的过载能力;而高过载倍数时,电动机绕组近似在绝热情况下发热,动作时间应短一些。通常模拟电子式保护器(如OMROW的J7T型)的反时限形成电路如图2所示,所生成的保护规律具有电流一次方对数特性,见图1中曲线2。 

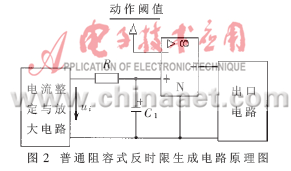
　　这种电路生成的保护特性具有一定的局限性,主要是低倍过载时动作时间太短。若解决这一问题,最直接的办法是设置两个时间常数,令低倍过载时的时间常数τ值大一些,使低倍过载时的保护特性尽量逼近标准的保护特性;而高倍过载时的τ值小一些,这样就有可能生成一种理想的保护特性。基于这种思想,对图2电路进行了改进。改进的反时限形成电路见图3。电路仅增加了一只稳压管和一只电阻,稳压管电压V_DW取2倍过载时对应的信号电压。这一电路的工作原理是:当低倍过载时,稳压管不起作用,阻容电路的时间常数为τ=(R₁+R₂)C₁;而高倍过载(I/I_e≥2)时,信号电压将增大而使稳压管击穿,此时的电路时间常数变为τ=R₂C₁，相当于从低倍过载到高倍过载执行了两个时间常数。当稳压管为理想稳压管时,在理论上,其动作特性被分成两段,如图4所示,曲线3为低过载倍数大时间常数的曲线,而曲线2为高过载倍数小时间常数的曲线。但实际上稳压管在齐纳击穿之前就有了渐渐增加的漏电流,其反向伏安关系如PN结的指数型伏安特性。随着信号电压ui的增加,反向电阻渐渐减小,相当于阻容电路的时间常数渐渐地由大变小,亦呈现指数型规律。这样,理论上分段时间常数的阻容式保护特性就变成了实际上指数型时间常数的过度平滑的保护特性,如图5中曲线3所示。 

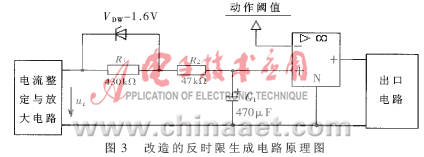
　　改进后的保护特性与标准保护特性及J7T型保护特性三者相比较,结果见图5。从图中可以看出,改进后的特性3曲线不再平坦,具有了准二次方的特性。而与标准特性1相比,虽然略有差异,但低倍过载段却更具实用性。低倍过载时的动作时间变长,更有利于电动机正常过载能力的发挥。研究表明,对于中小型电动机,在低倍过载时,其实际的热特性是大于电流二次方特性的^[2]。而高倍(≥2倍)过载时曲线3与标准特性1非常接近,明显优于单纯一次方规律的曲线2,自然可以有效地保护电动机。 

　　利用稳压管PN结的反向指数型伏安特性对阻容式电动机热保护装置的反时限特性进行改进以后,其动作特性发生了根本性的变化,改进后的动作特性更接近于标准特性,更具有实价值用。而改进后的电路非常简单,不会影响保护装置的体积和成本。对于量大面广的中小型电动机,这样的保护特性无疑是较为理想的。 

参考文献 

1 童诗白.模拟电子技术基础(第二版).北京:高等教育出版社,1988 

2 马少华.电动机热特性及其过载保护.中国电工技术学会,低压电器专业委员会第七界学术年会论文集，1995.6 

3 Ma Shao-Hua. Research of Thermal Characteristics of Electric Motor.Third International Conference on Electrical Contacts， Arcs， Apparatus and their Application，Xi＇an， P.  R. China， May，1997 

4 国际标准.  IEC255-8