摘 要: 在MCL算法的基础上,结合改进的基于多维定标MDS(Multidimensional Scaling)的定位算法引进新的滤波条件,提出了一种移动节点定位算法。该算法通过在循环滤波部分引入新的限定条件,可以保留更靠近真实距离的预测样本,减小定位误差。仿真实验表明,该算法具有更好的定位精度。
关键词: 无线传感器网络;移动节点;定位算法;蒙特卡罗;多维定标
无线传感器网络WSN(Wireless Sensor Networks)综合了无线通信技术、传感器技术、嵌入式计算技术和分布式信息处理技术,已经成为当前国际上备受关注的、多学科高度交叉、知识高度集成的前沿研究领域[1]。通过部署大量传感器节点至目标区域,WSN将改变人们与客观世界的交互方式,其在环境监测方面的应用尤其具有广泛前景[2]。
鉴于WSN的应用背景,定位技术成为实现其功能的关键技术之一,如何使定位指标达到最优始终是WSN定位算法的研究目标。
近年来,对WSN定位问题有了许多新颖的思想和解决方案,但多是针对解决固定节点的定位问题。若将这些算法应用于移动节点的定位,虽然也可以通过每隔一段时间的更新来进行定位,但节点的移动性会导致算法的定位精度降低。虽然移动性给节点定位带来了困难,但也可以利用其来提高定位精度。参考文献[3]提出了一种基于MCL(Monte Carlo Localization)的移动节点定位算法,其核心思想是在贝叶斯滤波位置估计基础上,用若干个带权重的采样点来描述移动节点在布置区域的可能位置分布。
多维定标技术MDS(Multidimensional Scaling)是一种运用于心理学领域的技术,后由Shang等人引入WSN定位技术中[4]。基于MDS技术的定位算法在不需要知道节点间测量距离的情况下,可以充分利用节点间连通性信息,在即使没有锚节点的情况下也可以得到节点的相对位置坐标。
本文提出一种MDS-MCL定位算法,通过结合MCL和MDS-RC[5]两种方法,得到一种新的移动节点定位算法。通过将MDS-RC定位算法引入MCL算法,在定位过程中利用MDS-RC定位算法给出的定位位置作为新的限定条件进行滤波,保留更接近节点真实位置的预测样本,提高节点定位精度。
1 MDS-MCL定位算法
本文提出的MDS-MCL算法,主要是通过在过滤阶段利用MDS-RC算法给出的定位结果作为新的限定条件,滤除预测样本,以达到提高精度的目的。
1.1 引入新的滤波条件
MDS-RC定位算法是一种应用在大规模固定节点定位问题中的算法,通过对节点间最小路径赋予权值的方法来提高算法的整体定位精度。在大规模的网络中使用时,该算法的整体定位效果较好,但不排除出现个别节点误差较大的情况。在大规模网络中,由于整体定位精度较高,所以即使个别节点的定位误差较大,也不会影响算法整体的定位效果。但将这种算法应用于单一节点的定位时,这种偶然出现的较大误差对于最终定位结果的影响较大,必须进行处理。
在MDS-MCL定位算法中,会对MDS-RC得到的定位结果进行判断,根据不同的情况采取不同的滤波方式,从而避免偶然出现的大误差对最终结果造成影响。算法的具体流程如图1所示。

算法的初始化主要是进行循环次数k和预测样本总数N的设定。
如图1所示,在每一时刻的定位过程中,首先根据周围一跳范围内的信标节点信息,根据MDS-RC算法,得到初步定位位置ot。然后根据ot是否在最大移动速度范围内对预测样本进行处理。
过滤阶段的详细处理方法如下:
第一种情况:如果算法的定位位置ot在最大移动速度范围内,则根据ot进行滤波。在生成的N个预测位置中,计算其与ot的距离,将这些距离与前一次保留的预测样本进行比较,保留N个与ot最近的样本,然后进行下一次循环。
第二种情况:如果算法的定位位置ot在最大移动速度范围外,用另一种方法对位置进行修正。在使用MDS-RC算法进行定位时,会利用到周围一跳范围内的信标节点。对预测样本中的每一个位置,统计在其通信范围的本次定位中利用到的信标节点数,然后与前一次保留的预测样本进行比较,保留N个信标节点数最多的样本,然后进入下一次循环。
通过结合MDS-RC与MCL方法对移动节点进行定位,可以避免单一方法中偶然出现的较大误差。
另外,MDS-MCL算法与MCL算法另一点不同的是,在每一次滤波中保留N个最符合要求的预测样本,而不是严格删除所有不符合要求样本。通过这一点修改,可以保证算法在规定次数的循环内得到足够数量的预测样本,从而将算法的计算时间控制在一定范围内。
1.2 参数与算法表现的关系
在MDS-MCL算法中,有两个初始参数:循环次数和预测样本数。为了使算法的性能达到最优,下面通过仿真实验考察这两个参数对定位误差和计算时间的影响。



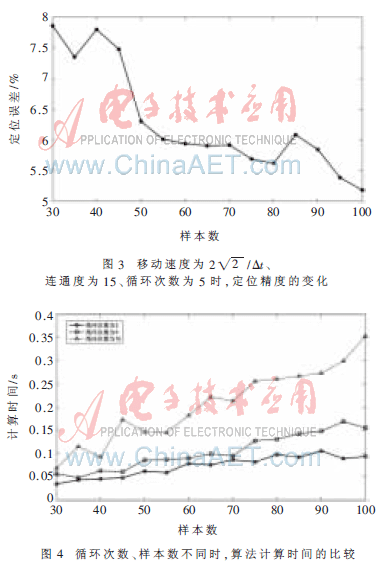
在移动节点的定位中,必须要考虑实时性因素,图4给出了在循环次数、样本数不同时定位时间的变化。由仿真结果看出,当循环次数为3和5时,算法的计算时间较短,且随样本数的增长变化较为平缓,当循环次数为10时,计算时间略长,且随样本数变化的较为剧烈。
综上所述,为了兼顾定位精度和计算时间两方面的考虑,在参数的选择中,可将样本数选为50,循环次数选为5。
2 算法仿真实验及结果
在本文中,通过MATLAB7.0软件进行仿真实验,节点被随机部署在范围为100×100网络中,信标节点的位置固定,均匀分布在整个网络中。节点的通信半径设为20。在仿真试验中,通过改变部署的节点总数来改变节点连通度(平均每个节点具有的邻居节点数)。
本文中,移动节点定位误差定义如下

为了说明MDS-MCL算法的性能,将其与MCL定位算法进行比较。
图5为移动速度不同时,各连通度下两种算法的定位误差。
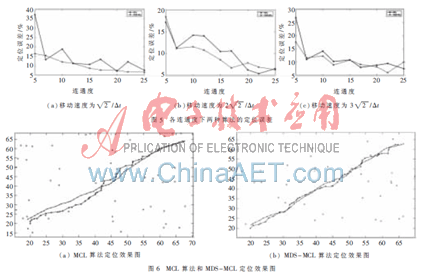
由图中可以看到,MDS-MCL算法相对普通的MCL定位算法,具有更好的定位精度。且在各连通度下,节点的定位误差基本稳定,基本保持在10%左右,比MCL算法有了2%左右的提高。
图6(a)和图6(b)给出了在最大移动速度为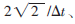 连通度为15时,MCL算法和MDS-MCL算法的定位效果图。可以看出,经过改进后的定位算法对移动节点的运动轨迹拟合更好。
连通度为15时,MCL算法和MDS-MCL算法的定位效果图。可以看出,经过改进后的定位算法对移动节点的运动轨迹拟合更好。
在基于MCL方法的基础上,本文结合MDS-RC方法对移动节点定位算法进行了改进。通过仿真可以验证,即使在不需测距的情况下,移动节点也可以得到较好的定位效果。通过将MCL算法和MDS-MCL算法进行比较,可以验证改进算法的定位误差大体均在15%以下,且相对前者有2%左右的降低。另外,通过对算法计算时间的考察,可以验证改进算法的计算时间较短,可以满足实际应用的要求。
参考文献
[1] Liu Yongmin, Wu Shuci, Nian Xiaohong. The architecture and characteristics of wireless sensor network[A]. In: Proc. of the 2009 Computer Technology and Development (ICCTD’09) Conf. Vol.1[C]. Kota Kinabalu, 2009:561-565.
[2] Wu Zhengzhong, Liu Zilin, Liu Jun, et al. Wireless sensor networks for living environment monitoring[A]. In: Proc. of the 2009 Software Engineering(WCSE’09) Conf. Vol.3[C]. Xiamen, 2009:22-25.
[3] Hu Lingxuan, DAVID E. Localization for mobile sensor networks[C]. In: Proc. Of the 10th Annual International Conference on Mobile Computing and Networking(MobiCom-2004), 2004:45-47.
[4] SHANG Y, RuML W, ZHANG Y. Localization from mere connectivity in sensor networks[C]. In:Proc. of the 4th ACM Int’l Symp on Mobile Ad Hoc networking ^computing, New York: ACM Press, 2003:201-212.
[5] Chen Bingjie, Huang Xiaoping, Wang Yan. A localization algorithm in wireless sensor networks based on MDS with RSSI Classified[C]. In: Proc of the 5th Hefei International Conference on Computer Science & Education(ICCSE’10), 2010:1465-1469.

