摘　要: 介绍了一种基于隐马尔可夫模型的轴承故障音频信号诊断方法。通过对轴承音频信号的Mel频率倒谱系数特征提取，分别采用离散HMM和连续高斯混合密度HMM两种方法进行建模与诊断研究。与CGHMM方法相比，DHMM方法运算速度快，但诊断精度低。而从总体上来看，两种方法都具有运算速度快，诊断精度高的优点。结果表明，本文方法具有很好的应用前景。 

    关键词: 轴承； Mel频率倒谱系数；隐马尔可夫模型； 音频信号

    轴承是机械设备中应用最为广泛的一种通用部件，也是最容易损坏的零件之一，它工作正常与否直接影响整台机器的性能，因而轴承故障诊断成为重要的研究课题和目前的研究热点^[1-4]。在轴承故障诊断研究中，通常是对其工作时产生的振动信号^[1]或音频信号^[2-4]进行分析，以判断轴承运行状态。振动信号法通过安装在轴承座或箱体适当地方的加速度传感器获取轴承振动信号，并对其信号进行分析与处理，进而判断轴承是否运行正常。此方法的不足在于需要将加速度传感器固定在待检测的设备上，增加了成本，使用也不方便。音频信号的采集属于非接触式，只需要利用麦克风作为声音传感器，不但使用方便而且成本低廉，具有振动信号不可代替的优势。参考文献[2-4]研究表明，当轴承运行状态发生变化，音频信号特性也会随之变化时，因而对音频信号分析是一种有效、可行的轴承故障诊断方法。目前，基于音频信号的轴承故障诊断方法主要有：小波分析^[2]、神经网络^[3]和盲源分离方法^[4]等。 

    隐马尔可夫模型HMM（Hidden Markov Model）是一种描述随机过程统计特性的概率模型，能够对多个观察样本进行有效融合而构成一个模型，具有较好的抗噪能力，在交通监测^[5]、图像识别^[6]、语音识别^[7-8]以及基于振动信号的故障诊断^[1]等领域中都得到了较好的应用，也是目前为止最有效的语音识别方法。而Mel频率倒谱系数MFCC(Mel Frequency Cepstrum Coefficients)考虑了人耳听觉特性，能很好地反映音频信号特征，在语音识别、音频分类和检索研究领域应用十分广泛[8]。本文通过对音频信号的MFCC特征提取，分别采用DHMM(Discrete HMM)和CGHMM(Continuous Gaussian Mixture HMM)两种方法进行建模与诊断研究。DHMM方法对观测序列进行了量化处理，运算速度快，却降低了诊断精度。而CGHMM方法不需要量化，避免了量化带来的数据处理误差，提高了诊断精度，但减慢了运算速度。从总体上来看，两种方法都具有运算速度快、诊断精度高的优点，具有很好的应用前景。 

1 理论基础  

1.1 MFCC 

    Mel频率倒谱系数MFCC用于信号特征提取，其计算过程如下^[8-9]： 

    (1) 确定每一帧信号的长度N及帧移，并对每一帧信号序列进行预处理(加窗、预加重等)。本文采用应用较广的汉明窗： 

    ω(n)=(1-α)-αcos(2πn/N)                                (1) 

式中，0<α<1，通常取值为0.46。 

    (2) 将预处理后的信号进行快速傅立叶变换（FFT），将时域信号转换为频域信号,再计算其模的平方得到能量谱P[k]，0≤k≤N-1。 

    (3) 选取滤波器个数为M，并定义最低频率接近零，最高频率为输入音频信号频率的一半，再根据mel(f)频率与实际线性频率f的关系mel( f )=2 595lg(1+f/700)计算出三角带通滤波器组H_m[k],则能量谱P[k]通过三角带通滤波器组H_m(k)后的输出为： 

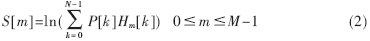
    (4) 对S[m]进行离散余弦变换（DCT）即得到MFCC系数: 

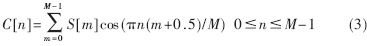
    (5) 取C[1],C[2],…，C[V]作为MFCC参数，此处V是MFCC参数的维数，通常为12～16。 

1.2 HMM 

    隐马尔可夫模型HMM是在Markov链的基础上发展起来的一种概率模型，由三个基本参数来描述。第一个参数为状态转移概率A={a_ij|1≤i,j≤N}，a_ij=P(q_t+1=S_j/q_t=S_i)表示从状态S_i变化到状态S_j的转移概率，显然且a_ij≥0，其中，q_t表示Markov链t时刻所处的状态，N为HMM状态数。第二个参数为观察值概率分布B={b_j(k)|1≤j≤N, 1≤k≤M}，b_j(k)=P(O_k/q_t=S_j)表示进入状态S_j时输出为O_k的概率，O_k表示观察值，M为可能的观察值数目。根据观察值序列的分布特点，HMM模型可分为离散DHMM和连续DHMM两大类。同时，如果观察值序列服从连续高斯混合密度函数分布，则为连续高斯混合密度CGHMM。最后一个参数是初始概率分布π={π_i|1≤i≤N}，π_i=P(q₁=s_i)表示Markov链从状态S_i开始的概率，显然 

    有了如上定义，HMM可描述为: 

    λ=(π,A,B)                                       (4) 

2 基于HMM的故障诊断 

    基于HMM的轴承故障音频信号诊断系统框图如图1所示，主要包括数据采集、特征提取、HMM训练和HMM诊断等部分。 

2.1数据采集 

    数据采集是使用麦克风作为声音传感器，将轴承的音频信号变为一定的电平信号输入计算机，即录制波形音频的过程。在数据采集之前，需要按照一定规则设定好音频信号几个重要的采集参数：采样频率、位数和声道数。本文在采样频率为22.05kHz、A/D转换精度为16位、声道数为单声道的条件下，采用VC++中提供的函数库，实现对轴承音频信号的数据采集。简单流程为：打开录音设备、准备WAVE数据头、准备数据块、开始录音、停止录音以及关闭录音等，详细过程请参见参考文献[10]。 

2.2 特征提取 

    特征提取是指从轴承音频信号中提取有用的统计数据，如Mel频率倒谱特征参数(MFCC)、线性预测倒谱系数(LPCC)、感觉加权线性预测系统(PLP)等,是故障建模与识别的关键，直接影响到故障诊断效果。此外，特征提取还可以用差分系数近似描述音频信号的帧间相关性，反映信号的动态特征。动态特征和静态特征互相补充，提高了系统的诊断性能。因为MFCC参数充分利用人耳的听觉特性，能很好地体现音频信号的主要信息，在语音识别、音频分类和检索领域应用十分广泛^[8]。所以本文选用12维MFCC参数和12维一阶差分MFCC进行诊断实验。 

2.3 HMM训练 

    HMM训练是指从同类故障的大量音频信号样本中提取统计信息，利用恰当的训练算法对模型参数反复修正直至收敛，最后得到模型的状态转移概率A、观察值概率分布B、初始概率分布π等参数。典型的训练算法有Baum-Welch算法，但此算法是在假定只有一个观察值训练序列的条件下得到的。为了增加HMM故障诊断系统的稳健性和提高故障诊断的准确率，需要选取多个样本进行训练，以建立轴承各类故障状态的HMM参数模型。记L个观察值序列(即L个样本)为O⁽¹⁾、O⁽²⁾、…、O^(L)，每个观察值序列的长度记为T，则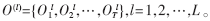此时，基于多观察值序列训练的重估公式可写为: 

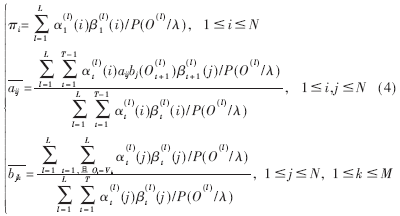
2.4 HMM诊断 

    训练完成之后将模型参数存储，此时，系统就具备了诊断的能力。诊断过程中，输入待检测轴承音频信号，经过预处理、MFCC特征提取后，得到观察值序列O={O₁,O₂,…,O_T}。然后，对此观察值序列进行故障检测，当检测到有故障发生时，再进一步进行故障诊断，判断出音频信号的故障类型。 

    (1) 故障检测 

    故障检测只需要训练一个代表轴承正常状态的HMM模型，记为λ₀。根据前向-后向算法^[8]计算出待检信号O={O₁,O₂,…,O_T}在正常模型λ₀下的输出概率P(O/λ₀)。如果此概率P(O/λ₀)大于预先确定的某一阈值，则表明轴承工作正常;否则，轴承有可能出现某种故障，需要进一步进行故障诊断。 

    (2) 故障诊断 

    同样使用前向-后向算法^[8]，快速有效地计算出观察值序列O={O₁,O₂,…,O_T}在各HMM模型下的输出概率，通常情况下，概率最大的模型即为诊断结果。为了提高系统的诊断精度，可在后处理阶段辅以必要的拒识算法，比如设定适当的概率阈值，如果最大概率小于这个阈值，则诊断为其他运行状态。 

3 轴承故障诊断实验 

    在Visual C++7.0环境下，自主开发了基于HMM的音频故障诊断平台，本文所有实验均在此平台上完成；诊断对象为6202CM深沟球滚动轴承，其转速为1800r/m；采样频率为22.05kHz；A/D转换精度16位；数据帧长512，帧移128。通过特征提取，将每帧信号都转换成12维MFCC和12维一阶差分MFCC，形成长度为32的观察值序列，分别采用DHMM和CGHMM两种方法进行了建模与诊断实验。 

    在模型训练环节，对于正常声音、内圈异音、外圈异音、滚动体异音以及保持架音等五种轴承状态，各采集30组音频数据样本进行训练，分别得到DHMM和CGHMM两类模型训练过程，两种故障模型的平均训练时间如表1所示。由表可以看出，由于DHMM对观测序列进行了量化处理，计算量小，训练速度快；而CGHMM的复杂度比较高，收敛过程长，比DHMM方法的训练时间多出近一倍(但也在实时要求之内)。 

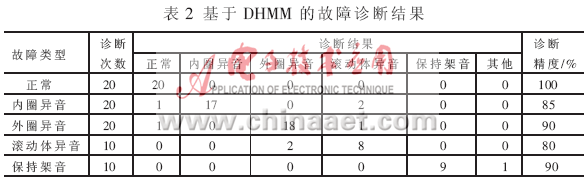
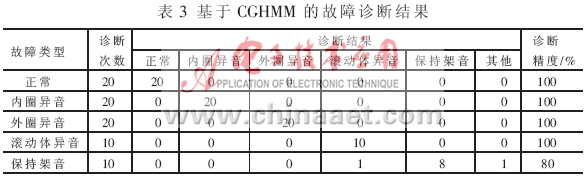
    在诊断环节，另外采集了20组正常声音、内圈异音、外圈异音以及10组滚动体异音和保持架音等五组数据分别进行了测试，得到的基于DHMM和CGHMM的故障诊断结果分别如表2和表3所示。在DHMM方法中，共80次诊断出现8次误诊，总的诊断精度接近90%，效果较良。而CGHMM方法只出现2次误诊，诊断精度达到了97.5%，明显高于DHMM方法，更具有良好的应用前景。 

    本文在VC++平台下，自主开发了一套基于HMM的轴承故障音频诊断平台。通过对音频信号的MFCC特征提取，分别采用DHMM和CGHMM两种方法进行建模与诊断研究。由于DHMM方法对观测序列进行了量化处理，运算速度快，但降低了诊断精度。而CGHMM方法不需要量化，避免了量化带来的数据处理误差，提高了诊断精度，但减慢了运算速度。从总体上来看，两种方法都具有运算速度快、诊断精度高的优点，具有很好的应用前景。 

参数文献 

[1] OCAK H, LOPARO K A. A new bearing fault detection  and diagnosis scheme based on hidden markov modeling of vibration signals [A]. IEEE International Conference on Acoustics, Speech, and Signal Processing, 2001,(5):3141-3144. 

[2] 周艳玲，杨德斌，徐金梧,等．基于声信号的轴承故障诊断方法[J]．振动与冲击, 2002,21(2):21-23. 

[3] 李良敏．基于遗传算法的盲源分离在轴承诊断中的应用[J]．轴承,2005,(9):31-34. 

[4] 高向东，黄石生，高存臣．神经网络及声谱分析技术在轴承故障诊断中的应用[J]．轴承, 1996,(8):2-5. 

[5] JIEN K, WATANABE T, RITTSCHER J, et al. An HMM-based segmentation method for traffic monitoring movies [J]. IEEE Trans on Pattern Analysis and Machine Intel, 2002,24(9):1291-1296. 

[6] LIU N J, DAVIS R I A, LOVELL B C, et al. Effect of initial HMM choices in multiple sequence training for gesture recognition[A]. International Conference on Information Technology, 2004:608-613. 

[7] 谢锦辉．隐Markov模型(HMM)及其在语音处理中的应用[M]．武汉: 华中理工大学出版社, 1995. 

[8] HUANG Hai Dong. Spoken language processing[M].Prentice Hall, 2001. 

[9] 陆汝华，杨胜跃，朱颖，等．基于DHMM的轴承故障音频诊断方法[J]．计算机工程与应用，2007,43(17):218-220. 

[10] 陆汝华．基于HMM的轴承故障音频诊断方法研究[D]:硕士学位论文． 长沙：中南大学出版社，2007.