摘 要: 为了提高实体反求的效率,提出一种点云简化方法。该方法通过建立点云的栅格化拓扑关系,有效地收集每个测量点的邻域点,并在邻域内建立局部坐标系。同时,拟合局部抛物面估算各个测量点的曲率值,并根据曲率变化收集形状特征点。最后,依据邻域内形状特征点的分布状况,对点云实施简化。该简化方法充分地保留了原始点云的形状特征,同时删除了大量的冗余点,具有一定的先进性,为反求工程的曲面重构提供了良好的基础。
关键词: 反求工程;点云;曲率;特征点提取
随着反求工程技术的发展,物体表面数据的采集方法越来越多样化,在引入了激光及其他光源技术后,三维测量设备得到了长足的进步,但其测量数据过于庞大,影响了后续的曲面重构处理的速度与效率,因此对点云进行简化非常必要。近年来,人们对三维数据的精简进行了大量地研究,CHEN Y H[1]等人将点云数据三角网格化,通过一种向量加权算法来减少三角形数量,达到点云简化的目的;Fujimoto和Kariya[2]在1993年提出一种保证减少数据点的误差处于给定公差范围内的方法;Hoppe[3]和Eck[4]等人采用的PM(Progressive Meshes)算法根据子区域的连续性来简化点云;张丽艳[5]在用Riemann图建立数据点间邻近关系的基础上,提出按简化后点的个数、点的密度阈值以及删除一点引起的法向误差的阈值三种准则对点云进行简化。以上几种方法对于表面不复杂、曲率变化不大的点云数据精简很有效,但对于曲率变化大、附加特征多的表面点云数据难以直接应用。针对以上方法的不足,本文提出一种新的数据精简方法。该方法根据物体形状尽可能多地保留了特征区域的数据,克服了数据表面曲率变化大对实物反求造成的影响,同时又删除了大量冗余数据,提高了点云简化的效率。
1 点云拓扑关系的建立
本文以没有任何拓扑信息的散乱点集为处理对象,首先建立散乱点的拓扑邻近关系,为避免在整个点集中寻找每个测点的K-近邻(K为测量点的邻域点数,根据后续邻域曲面拟合的一般取为10~20)。具体方法是:采用包围盒法[6]中空间栅格的划分策略,首先根据测点分布,形成一个与坐标轴平行的长方体包围盒,并将包围盒沿x、y、z轴划分成m×n×l个小立方体栅格,栅格宽度λ可根据实际点云的分布情况进行设置,一般设为点云分布密度的K倍。点云分布密度采用如下方法估算:在点云中随机取出N点,计算离点Pi最近点的距离di,则分布密度为: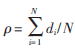 ;再根据每一个数据点的x、y、z坐标值将该数据点的序号追加到相应的栅格中,通过设置一个动态链表,记录数据点所在的坐标值和该点所在栅格的索引位置,从而建立起散乱点的空间拓扑关系,完成点云数据的空间栅格划分。每个测量点的K邻近可以由其所在栅格及其邻近的上、下、左、右、前、后共27个立方体栅格中查找,根据其空间距离大小顺序将邻近点的动态链表索引号存储在与测量点对应的数组中。从而建立起每个数据点的邻域关系。
;再根据每一个数据点的x、y、z坐标值将该数据点的序号追加到相应的栅格中,通过设置一个动态链表,记录数据点所在的坐标值和该点所在栅格的索引位置,从而建立起散乱点的空间拓扑关系,完成点云数据的空间栅格划分。每个测量点的K邻近可以由其所在栅格及其邻近的上、下、左、右、前、后共27个立方体栅格中查找,根据其空间距离大小顺序将邻近点的动态链表索引号存储在与测量点对应的数组中。从而建立起每个数据点的邻域关系。
2 局部基面参数化
2.1 拟合微切平面
用局部的拟合曲面来估算曲率,首先需要对点云进行参数化。由于点云是散乱分布的,没有一定的特殊模式排列,所以点云的参数化十分困难。本文提出了一种简单的参数化方法,即建立局部微切平面,把散乱的点云投影到微切平面上,利用投影点来建立坐标系。微切平面方程可由平面的法矢量和平面上的一点表示,即:


其中,K1、m1分别表示最小曲率及其方向,K2、m2分别表示最大曲率及其方向,K为高斯曲率,H为平均曲率。
4 点云简化
一般点云简化的基本要求是既能缩减规模、消除冗余的点,又能保持整体形状、突出关键特征。传统的点云简化算法往往依据点云表面数据的平坦程度来设置一个阈值,以此来决定删除或保留的点。这种方法虽然对点云的数量进行了一定量的简化,但会削弱特征,引起整个形状改变,且会在某些曲面形状变化较缓同时又具有重要工程意义的区域(如平面与曲面的过渡区)造成过度简化。因此,简化过程最好能减少因简化导致的形状缺失及形状改变,尽可能地保留其特征细节。
为此,本文首先在每个测量点的邻域内拟合抛物面,估算出每一个测量点的曲率,然后对曲面过渡区、特征棱线和高曲率区的特征区数据点进行标记。特征区数据点即为曲率极值点(测量点的两个主曲率(K1和K2)中任何一个沿着对应的主方向上为极值)。曲率极值点可以采用如下方法收集:首先为各数据点的平均曲率H设定一个阈值,如果某点的平均曲率大于阈值,则作为候选特征点,实际特征点在候选特征点内产生。只要候选特征点中某一点的两个主曲率中任何一个沿对应的主方向为极值,那么就可以将该点定义为特征点。选取一候选点X沿最小曲率方向m1,找到左右两个邻接点X11、X1r,如果K1(X)≤K(X11)、K1(X)≤K(X1r)(其中,K(X11)、K(X1r)分别为点X11、X1r沿最小曲率方向m1的曲率值),则该点就是实际的边界点;否则,沿最大曲率方向m2,找到该点左右两个邻接点X21、X2r,若K2(X)≥K(X21)、K2(X)≥K(X2r),则X也可以作为边界点。对所有的候选特征点进行以上判断,就可以收集到特征点集。
对所收集到的曲率极值点进行平均曲率排序,得出一个曲率均值,然后根据简化的比例,通过交互对这个曲率均值进行适当调整,调整后的曲率值即作为曲率初始阈值。把大于这个初始曲率阈值的标识为特殊点,然后统计各个测量点在其K邻域内特殊点所占比率,给定一个初始简化距离阈值,用初始简化距离阈值除以特殊点密度与1的差的绝对值就可以确定这个特定测量点邻域的简化距离阈值。最后按简化距离阈值对数据点进行简化,即将邻域点中小于这个简化距离的点删除。
5 应用实例
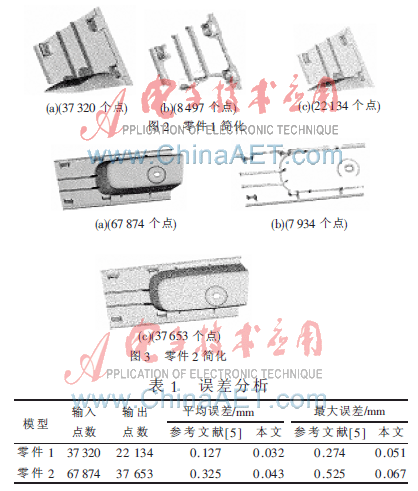
为了评估本文算法的性能,在Pentium4、1.60 GHz、512 MB内存计算机上运行,用C++语言在VC++6编译器上结合OpenGL库分别对零件1及零件2的点云模型进行了简化处理,图2、图3为点云简化的效果图,表1为计算结果。图2、图3均突出了特征点的提取,保证了曲率变化较大区域的保留,这说明在表达形状方面,本文的简化算法具有一定的准确性。图2(a)为零件1的原始点云图,共有37 320个点,图2(b)为提取的特征点,共有8 497个,图2(c)为简化后点云,共有22 134个,简化率为40%;图3(a)为零件2原始点云,共有67 874个点,图3(b)为提取的特征点,共有7 934个,图3(c)为简化后点云,共有37 653个,简化率为44%。由图2、图3可以看出,简化点云不存在简化后点云的局部过密或局部过稀的情况,而且依然保留了原始点云的基本特征,没有出现形状的缺失,对于曲率变化较大区域特征区域表达依然清楚。由表1可看出,对比参考文献[5],本文简化的方法在精确度方面具有一定的优势。
本文提出了一种点云简化算法,该方法首先采用包围盒法建立点云的空间拓扑关系;然后在此基础上建立点云的邻域,并在邻域内拟合切平面,利用邻域点在切平面上的投影点建立局部坐标;之后结合局部坐标拟合局部抛物面并计算曲率值,依据曲率变化的特征收集特征点,并依据特征点在各个测量点邻域内的分布情况对点云进行简化。该方法针对点云表面的形状特征,有选择性地对点云进行了简化,在曲率较大或尖锐棱边处极大地保留了点云的原始特征,使得最终的点云简化不会造成形状特征的缺失,同时又删除了大量的冗余数据,有效地对原始点云进行了精简。应用实例表明,本文提出的算法具有较高的效率,达到了预期的效果。
参考文献
[1] CHEN Y H, NG C T, WANG Y Z. Data reduction in integrated reverse engineering and rapid prototyping [J]. International Journal of Computer Integrated Manufacturing, 1999,12(2):97-103.
[2] FUJIMOTO M, KARIYA K. An improved method for digitized data reduction for computer integrated manufacturing[C]. International Conference on Industrial Electronics Control Instrumentation and Automation, 1992:896-901.
[3] HOPPE H. Progressive meshes[J]. Computer Graphics, 1996, 30:99-108.
[4] ECK M, DE D T, DUCHANP T. Multiresolution analysis of arbitrary meshes[C]. Proceeding of SIGGRAPH Computer Graphics, 1995:82-90.
[5] 张丽艳,周儒荣,蔡炜斌,等.海量测量数据简化技术研究[J].计算机辅助设计与图形学学报,2001,11(13):1019-1023.
[6] SUN W, BRADLEY C, ZHANG Y F, et al. Cloud data modeling employing a unified, non-redundant triangular mesh [J]. Computer Aided Design, 2001,33(3):183-193.
[7] 胡鑫,习俊通,金烨.反求工程中散乱点云数据的自动分割与曲面重构[J].上海交通大学学报,2004,38(1):62-65.
[8] 李江雄,柯映林.基于特征的复杂曲面反求建模技术研究[J].机械工程学报,2000,36(5):18-25.
[9] 朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2000.

