在用统计分析方法研究这个多变量的课题时,变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息方面尽可能保持原有的信息。
主成分分析(Principal Component Analysis,PCA), 将多个变量通过线性变换以选出较少个数重要变量的一种多元统计分析方法。又称主分量分析。在实际课题中,为了全面分析问题,往往提出很多与此有关的变量(或因素),因为每个变量都在不同程度上反映这个课题的某些信息。主成分分析首先是由K.皮尔森对非随机变量引入的,尔后H.霍特林将此方法推广到随机向量的情形。信息的大小通常用离差平方和或方差来衡量。
人们到医院就诊时,通常要化验指标来协助医生的诊断。诊断就诊人员是否患肾炎时通常要化验人体内各种元素含量,主要包括锌(Zn)、铜(Cu)、铁(Fe)、钙(Ca)、镁(Mg)、钾(K)及钠(Na)。表1是确诊病例的化验结果,其中1~30号病例是已经确诊为肾炎病人的化验结果,31~60号病例是已经确定为健康人的结果[2]。在论文中列出的数据是原始数据中1~10号病例及31~40号病例的数据,运用主成分计算时以所有数据为初始数据。

1 主成分分析模型
主成分分析是设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。通常数学上的处理就是将原来P个指标作线性组合,作为新的综合指标。最经典的做法就是用F1(选取的第一个线性组合,即第一个综合指标)的方差来表达,即Var(F1)越大,表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考虑选取F2即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不需要再出现在F2中,用数学语言表达就是要求Cov(F1, F2)=0,则称F2为第二主成分,依此类推可以构造出第三、第四,……,第P个主成分。

2 模型应用
2.1 问题分析解决

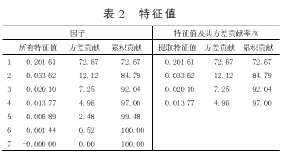
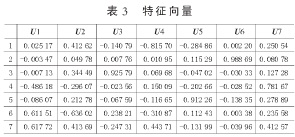
因C1=[X1 X2 … X7]*[U11 U12 … U17]T,因为特征值的方差贡献率为72.67 %,表明C1包含原变量中的绝大部分信息,则在原来7个因子的基础上引入C1作为第8个因子,C1=[0.70502、0.6341、0.87415、0.80724、0.4212、0.62897、0.37992、0.85489、0.57495、0.71527、-0.74635、0.03003、-0.30047、-0.03826、-0.80605、-1.32826、-0.5588、-0.00363、0.37216、-3.19199].再将其做标准化变化,再次通过主成分分析并结合SPSS软件确定B第一主成分F1、第二主成分F2和综合主成分F.根据对这8个因子通过SPSS的因子分析如表4、表5所示。

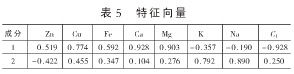
由表5可知C1与5种元素有着显着的相关性,可见许多变量之间直接的相关性比较强,证明它们存在信息上的重叠。
2.2 主成分表达式
主成分个数提取原则为主成分对应特征值>1的前m个主成分。特征值在某种程度上可以被看成是表示主成分影响力度大小的指标,如果特征值<1,说明该主成分的解释力度还不如直接引入原变量的平均解释力度,因此一般可以用特征值>1作为纳入标准。通过表4可知,提取2个主成分,即m=2.从表5可知C1、Zn、Cu、Fe、Ca、Mg在B第一主成分上有较高的载荷,说明B第一主成分基本反映了这些指标的信息,K、Na在B第二主成分上有较高的载荷,说明B第二主成分基本反映了K、Na 2个指标的信息。所以提取2个主成分是基本反映全部指标的信息,所以决定用2个新的变量来代替原来的8个变量。通过SPSS将表5中的数据除以主成分相对应的特征值开平方根,得到两主成分中每个指标所对应的系数。将得到的特征向量与标准化后的数据相乘,然后就可以得到主成分表达式:
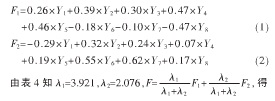
![]()
由(1)、(2)、(3)式得到B第一主成分F1、B第二主成分F2和综合主成分F的数据及排名,如表6所示。
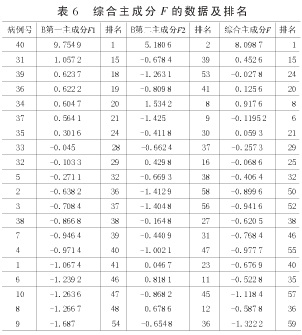
由表6可以看出第一主成分中以0为临界值,0.1为修正值,即(-0.1,0.1)为不稳定状态,此状态下的就诊人员将随机被确定为患者和健康者中的1个。而当F1>0.1时,将此时对应的就诊人员确定为健康者;当F1<-0.1时,将此时的就诊人员确定为患者。经此方法判定的患者与健康者与表1中的患者与健康者基本一致,并且与用综合主成分分析得到的结果基本一致。其判定的准确性可以达到95%以上,因此具备很强的可信性与科学性。
本文创新点在于模型中连续做了2次主成分分析,即二次主成分分析,并伴有大量的数据处理和数据分析,合理的结论背后拥有强大的理论支持和数据支持,具有很强的科学性和可信性。不过,确诊病人还是需要通过医生的具体分析,以达到所需效果。

