摘  要： 在分析Gabor小波的基础上，提出了一种变采样率Gabor小波的方法，与传统的Gabor小波相比，其识别效果得到大幅提高。该方法采用Curvelet、Log-Gabor小波和Contourlet三种方法结合主分量分析应用于人脸识别。对比实验结果表明，针对表情变化，Curvelet变换不仅识别性能最佳、速度也最快；而针对光照变化，Contourlet综合性能最好，对光照变化具有较强的鲁棒性。综合而言，使用Contourlet变换对图像进行特征提取效果非常好，它能很好地表达人脸的主要信息，是对人脸图像的一种稀疏的、有效的表达。
关键词： 多尺度几何分析；Curvelet变换；Gabor小波；Log-Gabor小波；Contourlet变换；主分量分析

　人脸图像易受到光照、表情、姿态以及背景等条件的影响，而且其本身也是一个复杂的特征空间，若直接使用原始的人脸图像进行识别，所取得的识别效果将受到限制。现在的一种常用做法是，对原始的人脸图像作某种变换，使得人脸图像从一个特征空间变换到另一个特征空间，以获得更好的识别效果。虽然小波变换因其具有强大的时频局域化性能而应用于人脸识别研究领域，但由于人脸图像更多的是面部轮廓和五官的曲线信息，而小波变换只能反映“点”的奇异性，难以表达图像边缘的方向特性，不能充分利用数据本身特有的几何特征，因此并不是最优的或者说“最稀疏”的函数表示方法。为了克服小波变换的不足，人们提出了基于小波变换技术基础上的系列变换，如Curvelet、Ridgelet、Contourlet等，统称为多尺度几何分析方法。多尺度几何分析发展的目的和动力正是要致力于发展一种新的高维函数的最优表示方法。本文所采用的Curvelet、Gabor小波、Log-Gabor小波和Contourlet变换，由于考虑了尺度、方向、角度等信息，而使得其在表达图像中的曲线时优于小波变换。事实上，在近二十年的人脸识别研究中，针对小波方法已有大量研究，重点围绕在小波基的选取、与子空间的结合以及在光照、姿态、表情影响下小波频带的选择等问题，此类工作已由戴道清给出了完整的综述[1-2]。但对于基于Gabor小波[3]、Log-Gabor小波[4]以及多尺度几何分析工具(如Curvelet[5-8]、Contourlet[9-10]等)方法的人脸识别尚未有全面的比较和研究。本文以此为出发点，对这几种多尺度分析工具在人脸识别中的应用进行了比较研究。

　式中，ω0为滤波器的中心频率，β为滤波器带宽。为了保证滤波器的形状恒定，对于不同的中心频率ω0，β/ω0必须保持不变。例如，当β/ω0为0.74时，大致相当子滤波器为1倍频的带宽；为0.55时，相当于2倍频；为0.41时，相当于3倍频。
3 Curvelet小波
　传统的小波变换只能反映“过”边缘特性，而且小波的变换核是各向同性的，无法更精确地表达图像边缘的方向特性。因此，Donoho等人提出了曲波(Curvelet)变换。Curvelet变换直接以边缘为基本表示元素，具有很强的方向性，非常有利于图像边缘的高效表示，它是一种多分辨、带通、具有方向性的函数分析方法，符合生理学研究指出的“最优”图像表示方法应该具有的三种特征。
　Curvelet变换是改进型的分块方法，即首先对图像进行子带分解，然后将不同尺度的子带图像分成大小不同的子块，分别对每个子块进行脊波变换(脊波变换是曲波变换的核心)。Curvelet变换的一个最核心的关系是Curvelet基的支撑区间有：widthα~length2。称这个关系为各向异性尺度关系，这一关系表明Curvelet是一种具有方向性的基原子。2005年CANDES E J和DONOHO D L等人提出了两种基于第二代Curvelet变换理论的快速离散实现方法[11]，本文采用的是其中的一种USFFT算法。
4 Contourlet变换
　Contourlet变换是在继承小波变换多尺度分析思想基础上，引入多方向性并由DO M N[12]和Martin Vellerli提出，是一种具有多分辨、局部、多方向的图像表示方法，一种“真正”的图像二维表示方法。变换的最终结果是使用类似于轮廓(Contour Segment)的基结构来逼近原图像，这也是Contourlet名字的由来。其基函数支撑区间的长度比随尺度变换而变换，表现为“长方形”，已达到用最少的系数来逼近奇异曲线，能以接近最优的方式描绘图像边缘。基的“长方形”实际上是“方向”性的一种体现，也称这种基具有“各项异性”。
　Contourlet变换分解过程是将多尺度分解和方向分解分开进行，如图1所示。在实现上采用了塔形方向性滤波器组(PDFB)，PDFB具有双叠代滤波器结构，将不同尺度的图像分解成方向子带。首先由LP(Laplacian Pyramid)变换对图像进行多尺度分解以“捕获”点奇异，分解得到一个近似信号(低频子带)和细节信号(高频子带)，接着将细节图像进一步送入方向滤波器组DFB (Directional Filter Bank)，将分布在同方向上的奇异点合成为一个系数，得到各方向子带信号，近似信号如此重复上一级操作，从而实现对图像多尺度多方向分解。

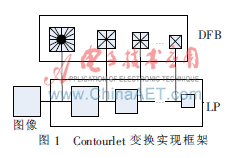
5 人脸库
　本文应用Yale和CAS-PEAL人脸库。Yale人脸库为众多研究者所熟知，多次应用在人脸识别研究中，本文重点介绍如图2所示的CAS-PEAL人脸数据库。

　该数据库由中国科学院计算技术研究所-银晨科技面像识别联合实验室负责建立，收集并整理了1 040位志愿者的99 450幅头肩部图像，图像尺寸均为360×480。所有图像在专门的采集环境下采集，涵盖了姿态(Pose)、表情(Expression)、饰物(Accessory)和光照 (Lighting)四种主要变化(简称PEAL)，部分人脸图像具有背景、距离和时间跨度的变化。图2(a)为部分Expression子库图像，环境光照模式下，要求志愿者做出笑、皱眉、惊讶、闭眼、张嘴五种表情，这五种都是造成面部特征变化比较大的表情，有利于研究识别算法对表情变化的鲁棒性。图2(b)为部分Lighting子库图像，采集光照子库图片时，环境光源关闭，每次打开一个方向光源进行图片采集，9个摄像头都同时工作，每人采集9幅不同角度的面部图像。
6 实验结果及分析
　实验过程：本实验先选取标准人脸库中的图像并读入，接着使用各种多尺度变换得到人脸图像的系数。为了进一步降低维数，本文结合主分量分析PCA(Principal Component Analysis)进行特征提取，得到更有意义的特征，然后使用最近邻分类器进行匹配识别，最终得出识别率。
6.1 实验一
　采用各种方法结合PCA在Yale人脸库上进行实验。考虑到算法泛化能力(也称推广能力)的问题，严格地讲，训练集合中的图像与测试集合的图像物应该是不能有重叠的，因此选取Yale人脸库上每人的6幅图像作为样本集，5幅作为测试集，顺序循环，共11组。实验结果如表1所示。

　在实验中，将本文提出的变采样率Gabor小波与Gabor恒采样率进行了对比。首先，对用Gabor小波分解获得的不同尺度特征后的数据，采取变采样率抽取其有用特征。实验发现，采用变采样率比用恒采样率取得更高的识别率，但其高识别率是以识别速度为代价的。在Yale人脸库中，采用Gabor恒采样率方法时，样本集和库内测试集中，第4号和第7号对数据影响较明显，分析Yale人脸数据库后发现，第4号和第7号人脸半边脸有阴影，在进行特征提取后发现是因数据相差较明显造成的。其次，采用Log-gabor、Curvelet、Contourlet方法依然结合PCA在Yale人脸库上进行实验，在实验中，观察到数据变换不明显，说明这些方法对阴影图像有较好的处理，且这三种方法中，Contourlet变换的识别效果最好。
6.2 实验二
　采用各种方法结合PCA在CAS-PEAL人脸库上进行实验。在Expression子库中随机选取60人(男女各一半)，每人5幅，共300幅图像，选取每个人的3幅图像作为样本集，2幅作为测试集。在Lighting子库中随机选取50人(男女各25人)，每人9幅，共450幅图像，选取每个人的5幅图像作为样本集，4幅作为测试集。其实验结果分别如表2、表3所示。

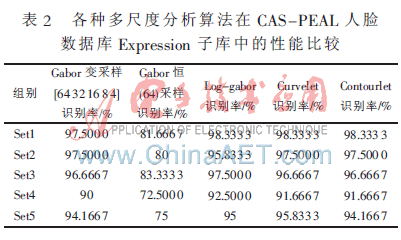
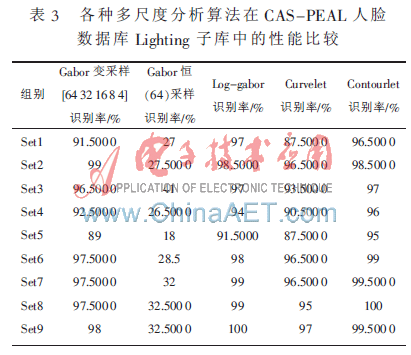
　在对CAS-PEAL人脸库表情变化较大的Expression子库实验中，发现利用Log-gabor、Contourlet、Curvelet方法结合PCA对人脸图像的识别率最高都达到了98.333 3%，其中Curvelet表现较为突出。在对光照变化较大的Lighting子库中，由于光照差别大导致面部图像的曲线发生了较大变化，从表3可以看出，采用Gabor小波恒采样率方法时识别率明显偏低，说明本方法对于光照变化比较敏感，而Contourlet变换的识别率最高(最高达到了100%)，最低识别率也达到了95%，说明该方法对光照有较好的处理。Log-gabor和Gabor wavelet变采样率也表现出了较好的特性，说明这几种方法对光照的鲁棒性都比较好。
　而不论在光照变化较大的Lighting子库还是在表情变化较大的Expression子库中，采用Gabor变采样率依然比用恒采样率取得更高的识别率。
　实验表明：(1)在算法运行速度方向，Curvelet变换最快，Gabor恒变换、Contourlet其次，而Gabor变采样率最慢。综上可知，在表情条件影响下，Curvelet变换表现最为突出，这一点不只表现在识别率上，也体现在识别速度上；而在光照条件影响下，Contourlet综合性能最好，它对光照变化具有较强的鲁棒性；(2)从比较实验的整体方面，使用Contourlet变换对图像进行特征提取效果非常好，能很好地表达人脸的主要信息，是对人脸图像的一种稀疏、有效的表达。然而，基于小波的人脸识别算法还有很多有待改进的地方，如具体的方向性特征系数选择对识别率的影响以及结合更有效的降维方法来进一步提高识别率和运算速度等方面还有待改进。
参考文献
[1] Dai Daoqing， YUEN P C. Wavelet based discrim inant analysis for face recognition[J]. Applied Mathematics and Computation， 2006， 175(1)：307-318.
[2] Dai Daoqing， Yan Hong. Face recognition[M]. Vienna，Austria： INTech Education and Publishing， 2007.
[3] 赵英男，孟凡斌，金忠.Gabor核函数窗的设置研究[J].计算机科学，2009.36(1)：111-113.
[4] FISCHER S. Self-invertible 2D Log-Gabor wavelets[J].  International Journal of Computer Vision， 2007， 75(2)： 231-246.
[5] CANDES E J， DONOHO D L. New tight frames of Curvelets and optimal representations of objects with c2 Singularities. http：//www.acm.caltech.edu/~emmanuel/papers/CurveE， 2002.
[6] CANDES E J， DONOHO D L. Curvelets-a surprisingly effecfive non-adaptive representation for objects with  edges[M].  In： Curves and Surfaces Nashville， TN：Vanderbilt Unit. Press， 2000：105-120.
[7] Zhang Jiulong， Zhang Zhiyu， Huang Wei， et al. Face recognition based on curvefaces[C].  Natural Computation， HAIKOU， 2007.
[8] 张九龙，张志禹，屈小娥，等.基于曲波与主分量分析的人脸识别[J].计算机应用，2008，28(5)：1255-1257.
[9] 夏思宇，李久贤，袁晓辉，等.一种基于Contourlet变换的人脸识别方法[J].信号处理，2008，24(4)：631-634.
[10] 林立宇.Contourlet变换影像处理应用[M].北京：科学出版社，2008.
[11] CANDES E J， DEMANE T L， DONOHO D L. Fast discrete Curvelet transform[R]. Applied and Computational Mathermatics. California Institute of Technology， 2005：1-43.
[12] DO M N， VETTERLI M. Contourlet-A directional multieolution image representation[C]. Prospect. of IEEE International Conference on Image Processing. Rochester， NY 2002：357-360.