基于改进遗传算法的圆阵稀布方法
2009-04-02
作者:包子阳, 陈客松, 何子述, 韩
摘 要: 由于圆形阵列所具有的特性,使其正得到日益广泛的应用,但是圆阵方向图却具有相对主瓣较高的旁瓣电平。为此,针对稀布圆形阵列的天线单元使旁瓣电平尽量降低的问题,应用改进的遗传算法,取角度差值为染色体的基因,进行阵列孔径、单元个数、最小间隔一定的稀布优化排列,减小了遗传算法的搜索空间,提高了搜索效率。仿真结果表明:该方法能有效提高收敛速度、降低圆阵的旁瓣电平。
关键词: 圆形阵列; 遗传算法; 方向图; 稀布阵列
一般情况下,由单个辐射器构成的天线就可以完成发射和接收电磁波的任务。但在一些特殊应用中,往往要求天线具有强大的方向性和很高的增益,有时还要求天线波瓣可以扫描,并具有一定的形状等等,这就需要利用多个辐射器即天线单元,按一定方式排列为天线阵列。排列在一条直线上的阵列,叫做线阵;排列在一个平面上的阵列,叫做平面阵;如果各个天线单元排列成一个圆环,就称之为圆阵。
目前的相控阵雷达天线基本上还是线阵和传统平面阵列天线。线阵列的结构相对来说比较简单,易于处理,但实际中它只能覆盖大约120°左右的方位角,所提供的增益和方向图等特性随扫描角的不同而改变,尤其是扫描角偏离阵列法线方向较大时,阵列性能急剧下降,所以大大限制了它的使用范围。传统的平面阵列同样也存在着一些类似缺点,如波束扫描范围窄、波束宽度随着扫描角的增加而增加、阵列单元之间的互耦效应等,使扫描角的函数难于保持平衡。
圆阵则有可能避免上述阵列的一些缺点。它不仅可以提供360°的方位角,而且可以通过循环移动阵列激励,简单而灵活地操纵波束的方位,在俯仰方向上也有一个理想的方向特性。同时,圆结构的对称性使其波束形状和天线增益等性能基本维持,并大体上保持互耦平衡。由于圆阵所具有的这些优势,使其正得到日益广泛的应用,但是圆阵方向图却具有相对主瓣较高的旁瓣电平,容易对信号的检测产生干扰。参考文献[1]中采用有向阵元来降低其旁瓣电平,但同时也降低了天线的增益。近年来利用稀布阵列单元来降低旁瓣电平的方法成为研究热点[2-8],但针对圆形阵列的研究还较少,本文采用改进的遗传算法,进行圆形阵列尺寸、单元个数、最小间隔一定的稀布优化排列,取得了较好的结果。
1 优化模型
考虑一圆形阵列半径R=m·λ,m为常数,λ为波长,由N个间距不同的天线元组成,di为第i个单元的方位角,波束指向为(φ0,θ0),则其方向图函数可表示为[1]:
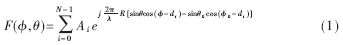
式(1)中, Ai为第i个单元权重的幅值,φ是起始于x轴正方向的方位角,θ是起始于z轴正方向的俯仰角,只考虑圆形阵列所在平面的方向图,此时θ=θ0=90°,则阵列方向图函数为[1]:

2 改进的遗传算法
遗传算法起源于对生物系统所进行的计算机模拟研究。生物的进化过程主要是通过染色体之间的交叉和变异来完成的。遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法,它借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法,它能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得最优解。遗传算法操作使用适者生存的原则,在潜在的解决方案种群中逐次产生一个近似最优的方案。在遗传算法的每一代中,根据个体在问题域中的适应度值和从自然遗传学中借鉴来的再造方法进行个体选择,产生一个新的近似解。这个过程导致种群中个体的进化,得到的新个体比原个体更能适应环境,就像自然界中的改造一样。
本文的改进之处在于取相邻两单元方位角度差值为染色体的基因,然后对其进行从小到大的排序,首行基因置零,这样可以缩小搜索区域,提高搜索效率。其流程图如图1所示。
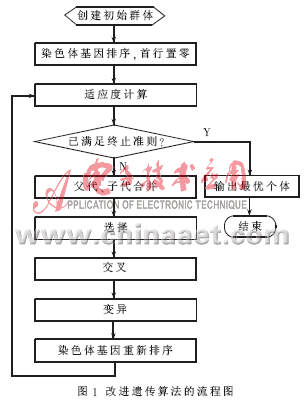
2.1 初始化
采用NP个维数为N的实数值参数向量作为一个种群,每个染色体表示为:

其中,i为染色体在种群中的序列,G为遗传代数,NP为种群规模。
为了建立优化搜索的初始点,种群必须被初始化。假定对所有随机初始化种群均符合均匀概率分布。参数变量的界限为0°
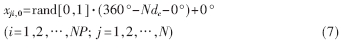
式(7)中:rand[0,1]表示在[0,1]之间产生的均匀随机数。
要满足式(4),需对每一个染色体的基因进行从小到大的排序和首行置零:

2.2 选择
采用基于排序的选择机制,其方法是先将群体中的染色体由好到坏排序(序号越小,相应的染色体越优),并定义序号i对应的染色体x(:,i)被选中的概率pi为[10]:

式(9)中, p是最优染色体被选中的概率,一般来说,取值较大时,尽管优良染色体被选中的机会多,有利于提高收敛速度,但群体缺乏多样性,易造成早期收敛。因此, p的取值不易太大,本文取p=0.05。再通过旋转赌轮选择染色体,具体过程是:对每个染色体x(:,i)计算累积概率qi
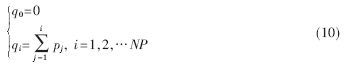
在区间(0,NP)内产生均匀分布的随机数r1;若qi-1
2.3 交叉
首先确定交叉操作的父代,从i=1到NP重复以下过程:在区间[0,1]内产生随机数r2,如果r2≤pc(交叉概率),则选择x(:,i)作为一个父代。再将父代染色体随机配对,并随机选择交叉位置进行单点交叉。如果进行交叉的染色体完全相同,则交叉不会产生新的模式,这类似生物界繁衍中的近亲繁殖。为了避免这种现象,在两个染色体进行交叉之前判断它们是否相同,如果不同,则直接进行交叉操作;如果完全一样,则随机产生一个新串替换一个父代再进行交叉。这种交叉方式可称为避同交叉。
2.4 变异
以变异概率pm在经过交叉的种群中选择进行变异的基因,其过程是从j=1到D,i=1到NP,在区间[0,1]中产生一个随机数r3,如果r3
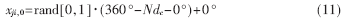
经过选择、交叉和变异操作,得到一个新的种群, 新生成的基因可能会不满足式(4)的要求,所以还要对每一个染色体的基因进行一次从小到大的排序(因首行一直为零,边界处理后还为最小值,所以不需将再首行置零)。

计算其适应度值然后与父群体合并,并且根据适应度值进行排序,进行下一次遗传操作。对上述步骤完成给定循环次数或满足一定的条件之后,遗传算法终止。
3 数值仿真
设一圆形阵列半径R=2λ,令其波束指向为(200°,90°),θ=θ0=90°对其进行相邻两单元间距离约为λ/2的均匀排列,可得所需单元数为24,此时阵列方向图如图2所示,最大旁瓣电平MSLL=-5.964 1dB。

对其进行单元数N=16、相邻两单元方位角度差值不小于dc=14.364 1°(距离为λ/2)的稀布排列,取种群中个体数目NP=100,最大遗传代数G=200,变量维数n=16,交叉概率pc=0.6,变异概率pm=0.01,主瓣的零功率点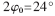 。
。
应用改进的遗传算法,优化后方向图的最大旁瓣电平MSLL=-11.346 8dB,其各单元的方位角度分别为[0°,16.352 4°,35.838 4°,50,666 9°,80.633 0°,120.418 0°,141.245 8°,172.042 7°,189.079 3°,204.505 2°,220.047 7°,238.136 3°,279.023 2°,296.797 9°,316.027 3°,339.377 7°]。图3是优化后的方向图。图4是4次独自应用改进遗传算法的适应度值曲线和其平均值的曲线。
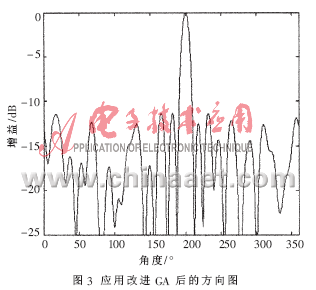
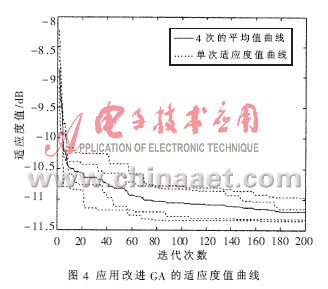
本文针对圆形阵列天线特有的角度特性,应用改进的遗传算法, 对其进行稀布优化排列,取相邻两单元方位角度差值为染色体的基因,将遗传算法的搜索空间从[0°,360°]减少到了[0°,360°-Ndc],提高了搜索的效率。仿真结果表明,该方法可有效地降低圆阵的旁瓣电平,为解决此类问题提供了有益的参考。
参考文献
[1] 刘先省,张连堂,吴嗣亮,等. 基于有向阵元的圆形阵列方向图综合[J].电子学报,2004, 32(4):701-704.
[2] CHEN Ke Song, HE Zi Shu, HAN Chun Lin. A modified real GA for the sparse linear array synthesis with multiple constraints[J].IEEE Trans Antennas Propag,2006,54(7):
2169-2173.
[3] CHEN Ke Song, YUN Xiao Hua, HE Zi Shu, et al. Synthesis of sparse planar arrays using modified real
genetic algorithm[J]. IEEE Trans Antennas Propag, 2007,55(4):1067-1073.
[4] 范 瑜,金荣洪,耿军平,等.基于差分进化算法和遗传算法的混合优化算法及其在阵列天线方向图综合中的应用[J].电子学报,2004,32(12):1997-2000.
[5] MURINO V, TRUCCO A, REGAZZONI C S. Synthesis of unequally spaced arrays by simulated annealing[J]. IEEE
Trans Antennas Signal Processing, 1996, 44(1):119-123.
[6] ANDREA T, VITTORIO M. Stochastic optimization of linear sparse arrays[J].IEEE Journal of Oceanic Engineering, 1999,24(3):291-299.
[7] PREETHAM B, BRANNER G R. Design of unequally spaced arrays for performance improvement[J]. IEEE Trans Antennas Propag, 1999, 47(3):511-523.
[8] DHANESH G K, MOHAMED H, ANDERS R. Synthesis of uniform amplitude unequally spaced antenna arrays
using the differential evolution algorithm[J]. IEEE Trans Antennas Propag, 2003, 51(9):2210-2217.
[9] 马云辉.基于遗传算法的唯相位控制方向图零点生成[J].微波学报,2001,17(2):41-46.
[10] 刘宝锭,赵瑞清.随机规划和模糊规划[M].北京:清华大学出版社,1999:15-36.

