摘  要： 针对EZW和SPIHT算法在压缩效率和压缩性能方面的不足，提出了改进算法，将(5,3)整数小波变化与这两种算法结合起来,并对三个子带分别进行编码，给出了两种算法的峰值信噪比、均方误差的理论对比分析。所有结论被 Matlab仿真试验验证。
关键词： 整数小波变化; 峰值信噪比; 均方误差; 均方根误差; EZW; SPIHT

    随着多媒体和通信技术的发展，人们对通信速度、数据的处理能力提出了近乎苛刻的要求。近年来针对图像压缩而提出的算法，既要能够有效地去除空间冗余、视觉冗余、时间冗余等各方面的冗余信息，还需充分考虑其压缩效率和解压缩效率，图像的失真度等各方面的因素。
    基于小波变换的图像编码技术主要是利用图像经过小波变换后的系数分布特点而得到不同的编码方案。EZW（嵌入式零树编码）和SPIHT（分层树集分割编码）是两种常见的基于小波变换的嵌入式零树编码方案。这两种编码方法不但实现了压缩比可调、分辨率可调，且压缩后的图像有很好的信噪比。因此现在很多图像压缩标准都采用了这两种编码方法。
    实验表明，EZW和SPIHT对三个子带取相同的熵值进行编码并没有充分表现出经过小波变换后图像子带间的相关性。同时SPIHT算法在实现上需要维护三个动态链表，占用大量的内存，不利于算法的实现和推广。基于以上两方面的缺陷，本文提出了改进算法。
1 算法简介及实现
1.1  整数小波变化
    研究图像压缩的编码方法，首先要选择合适的量化方案，将图像的空间域信息转换为频域信息。基于提升算法的整数小波变化，它既可以在多分辨率级上对图像进行分析，又不涉及浮点数的运算，不但简化了计算量,还可以用于无损压缩。其主要步骤如下：
    (1)分裂：将图像Sj=(ej-1,oj-1)分解为一个偶数序列和一个奇数序列；
    (2)预测：利用偶数序列去预测奇数序列，得到高频系数，dj-1=oj-1-P(ej-1)，对应图像的细节系数；
    (3)更新：预测后的图像可能出现某些特征系数与原图像并不一致，此时就需要更新操作Sj-1=ej-1+U(dj-1)。
    整个提升方案都是可逆的。
    由提升方案构造的（5,3）整数小波变换构造了双正交紧支小波基，它既可以用于无损图像压缩，也可以用于有损图像压缩。因此本文选择（5，3）整数小波变换作为图像的量化方案。    其算法实现过程如下：
  
  
       图1为lena经过三层(5,3)整数小波分解后的图像。

1.2  EZW算法
    经过小波变换后的图像分别在水平方向、垂直方向和对角方向连接，形成四叉树结构，如图2所示(Z字型为其扫描顺序)。
    具体步骤如下：
  
    (2)进行主扫描，比较小波系数和T值的大小，依次输出下列编码流，如图3所示；

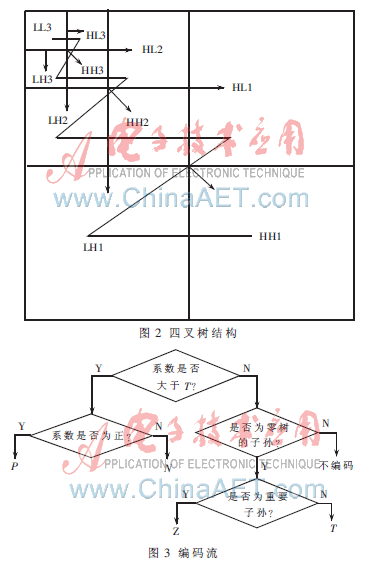
    (3)进行辅扫描，就是对系数P或N进行量化编码。
    每次扫描结束后只需将T（熵值）、scancode（主扫描表）、flaglist（辅扫描表）进行传输，EZW就是采用这种逐次逼近的嵌入式编码方式。
1.3 SPIHT算法
    SPIHT算法采用了与EZW算法相似的零树结构，它定义了三个动态链表LIS（无效集表）、LIP（无效像素集表）和LSP（有效像素表）。其中LIP和LSP中存储的是节点坐标，LIS中存储的是坐标集,其类型有L型和D型,L表示非直系亲属,D表示直系亲属。具体算法过程如下：
  
 else  output=0 add (k,l) to LIP
    ③如果LIS的类型为L
    if Sn(L(i,j))==1(each (k,l)∈O(i,j))
        output=1 and add (k,l)D to LIS
    else output=0
2 EZW和SPIHT算法的优缺点
2.1  EZW 算法的优点
    (1)利用经过小波变化后图像大部分能量集中在低频部分这一特点，进行有效的零树编码；
    (2)采用了SAQ（逐次量化逼近）的方法选择熵值，这样不但使压缩后的图像有很好的信噪比，而且也很好地利用了带宽，在传输图像的过程中首先接收到的是图像的轮廓部分，如果接收者认为不需要这幅图像可以中断图像的传输；
    (3)经过EZW编码后的图像，实现了分辨率可调、信噪比可调、压缩比可调；
    (4)使用自适应算法还可以使EZW算法应用于无损压缩。
2.2 SPIHT算法的优点
    SPIHT算法不仅继承了EZW算法的所有优点，还有如下优势：
    (1)采用了比EZW算法更细致的嵌入式比特流，使压缩后图像的信噪比更高；
    (2)每次只需要输出1 bit的信息流,在解码过程中不需要对信息流重新排列。
2.3 EZW算法和SPIHT算法的缺点
    (1)经过小波变换后图像的LL部分反映了图像的轮廓信息，聚集了压缩后图像的绝大部分能量，人眼对该部分的信息也较为敏感。EZW算法和SPIHT算法没有考虑到LL部分的重要性，使其解码后失真度较大。
    (2)经过小波变换后,图像在LH部分很好地保留了
垂直分界线,在HL部分很好地保留了水平分界线，EZW算法和SPIHT算法只考虑了子带间的相关，没有考虑子带内的相关性，对三者取相同的熵值进行编码，造成了压缩后图像的边界拓延性差。
    (3)在EZW算法中，如果一棵树的根节点是重要的，但是它所有的子节点都是不重要的，则需要4个0表示其子节点信息。同样在SPIHT算法中，如果一棵树的4个根节点不重要，但是它的子节点是重要的，则需要在LIP表中存储4个根节点信息。这样就造成了存储空间的浪费，也影响了编码和解码的速度。
    (4)在SPIHT算法中，需要维护三个动态链表，使SPIHT算法的实现受到了硬件的限制，不但增加了算法的复杂度，还造成了存储空间的浪费，阻碍了SPIHT算法的发展和推广。
3 改进算法
    针对上述不足，提出了以下改进方案。
3.1  改进方案1
    实验表明，EZW算法和SPIHT算法的复杂度随着某个位平面的重要系数个数的增加而增加。经过三层整数小波变换后的图像LL部分聚集了绝大部分能量，重要系数的个数也比其他子带要多许多。而且人眼对LL部分的信息较为敏感。考虑到LL3部分的重要性，本文将LL3部分单独编码并采用无损图像压缩编码的方法。
    经过整数小波变换后的图像其数据的浮动范围较大，在某种程度上影响了压缩的效果。因此本文增加了一个DPCM的预测过程，然后再对LL3部分进行Huffman编码。
    DPCM预测算法,以方便保留第一行和第一列的灰度值
    for i=m/8:(-1):2
            for j=n/8:(-1):2
                LL3(i,j)=LL3(i,j)-
    floor((LL3(i-1,j)+LL3(i,j-1))/2)
           for i=m/8:(-1):2
               LL3(i,1)=LL3(i,1)-LL3(i-1,1);
　　　        for j=n/8:(-1):2
                  LL3(1,j)=LL3(1,j)-LL3(1,j-1)
3.2 改进方案2
    考虑LH、HL、HH子带内系数的相关性，对三个子带取不同的熵值，然后再进行EZW或SPIHT编码。这样不但提升了解码的精度，还简化了运算。对于某个子节点(i,j)，其子节点为（2i,2j）(2i+1,2j)(2i,2j+1)(2i+1,2j+1),不需要再在子带内部求子节点。
3.3 改进方案3
    SPIHT算法在运行过程中需要维护3个动态链表，要实现该算法对硬件的要求较高，不利于该算法的实现和推广，因此本文选择了矩阵+链表的改进算法。将LIP和LSP都定义为一个矩阵，LIP是一个与图像大小一致的矩阵，用1 bit存储不重要系数标志位。LSP大小选择要根据所研究的图像来确定,对于每一个像素点需要用2 bit来存储其位置信息。动态链表LIS继续沿用原算法的定义。算法实现过程为：
　    (1)初始化：
       LIP={A1，A2，A3}(A1、A2、A3的大小与L3、L2、L1的大小相同)
　    LSP={B1，B2，B3}（这里取B1、B2、B3的大小为L3、L2、L1的1/4）
　    LIS=[(i,j,n)D/L](n表示层数)
　　(2)初始化扫描：图4为初始化LIP和LSP；图5为当LIS中n=1,type 为D的扫描方式；图6为当LIS中的n=1,type为L的扫描方式；图7为当LIS中的n=2，type为D的扫描方式。

　    (3)第二次扫描只有LIP的扫描方式有所不同，如图8所示。对LIS的扫描与上述一致。
    改进的EZW算法和SPIHT算法完整流程图如图9所示。

4 实验结果
      本文通过在Matlab2010a上编程实现了上述4种算法。
　    首先，从主观因素上对图像质量进行了分析，主要是在原算法和改进算法的扫描时间上进行了比较。
　　其次,从客观上对压缩后图像质量进行了评估，主要是通过PSNR(峰值信噪比)、MSE(均方误差）、RMS(均方根值误差)这三方面进行比较分析。
  
    RMS=((x1-x)2+(x2-x)2+…+(xn-x)2)/n (3)
    以下三组实验选择的图像大小为64×64×8 bit的国际标准测试图片lena、barb和boat，三幅图像的比特率均为0.25 bpp。
      表1为原EZW算法和改进算法在编码时间和解码时间的比较，图10为用原EZW算法和改进算法解码后的恢复图像，表2为用原EZW算法和改进算法对图像进行压缩后PSNR、MSE、RMS的对比。

    以下三组实验选择的图片大小为512×512×8 bit的国际标准测试图片lena、barb、boat。
    表3为原SPIHT算法和改进算法对实验图像进行不同比特率的编码后,在PSNR、MSE、RMS三方面的对比分析。
    图11为原SPIHT算法和改进算法对实验图像进行解码后的恢复效果图。这组实验选择的比特率为0.125 bpp。    图12为用原SPIHT算法和改进算法对实验图像进行解码后的恢复效果图。这组实验选择的比特率为0.25 bpp。

    基于整数小波变换的EZW算法和SPIHT算法不仅具有传统图像压缩算法的所有优点，而且还具有一些新的优点，如支持感兴趣图像编码，支持无损图像压缩等。本文以原EZW算法和SPIHT算法为基础，对图像进行三层(5,3)整数小波变换以后对低频部分进行DPCM+Huffman编码,将高频部分分为3个子带分别进行编码。同时摒弃了原SPIHT算法的三链表结构，采用了链表+矩阵的编码方式。图像在恢复效果和运行速度上都优于原算法。但是还有一些需要改进的地方，如EZW算法中如果一个根节点重要但是其所有的子节点不重要，如何有效地存储这个根节点，如何使压缩后图像有更好的压缩比和信噪比，有待进一步研究。
参考文献
[1] 赵荣椿,赵忠明.数字图像处理导论[M]. 西安:西北工业大学出版社,1999.
[2] 罗家辉,冯平,哈力旦.MATLAB7.0在数字图像处理中的应用[M].北京:机械工业出版社,2007.
[3] 冈萨雷斯.数字图像处理(第2版)[M].阮秋琦,译. 北京:电子工业出版社,2007.
[4] 张德丰. Matlab小波分析[M].北京:机械工业出版社, 2009.
[5] 和青芳.计算机图形学原理及算法教程[M].北京:清华大学出版社,2006.
[6] JPEG2000 PartI: Final draft international standard (ISO/IEC FDISI 5444-1)[S].ISO/IEC JTC1/SC29/WG1N18855,Aug.2000.
[7] ABU-HAJAR A, SANKAR R. Enhanced patial-SPIHT for lossless and lossy Image[C].ICASSP,2003.
[8] RANI B, BANSAL R K, BANSAL D S.Comparative Analysis of wavelet filter using objective quality measures[R].  International Advance Computing Conference,2009.
[9] SAID A, PEARLMAN W A. A new,fast,and efficient image codec based on set partitioning in hierarchical tree[J]. IEEE Trans.Circuits Syst.Video Techno[R]l,1996.
[10] 杨杰.数字图像处理及MATLAB实现[M].北京:电子工业出版社,2010.
[11] Jia Zhigang, Guo Xiaodong, Li Linsheng. A fast image  compression algorithm based on SPIHT[C].IEEE,2009.