基于差分进化的IRA码度分布优化
2009-04-07
作者:马 琦1,王海滨1,2,陈曾平1
摘 要: 针对一般LDPC码优化方法无法有效实现IRA码度分布优化的问题,提出了特定约束下IRA码度分布的优化方法。结合密度进化的高斯近似算法优化IRA码度分布序列,提取了IRA码检验矩阵构造的特定约束以改进差分进化算法。仿真结果表明,所设计的度分布序列的噪声门限高且搜索时间比改进前减少30%。
关键词: 低密度奇偶校验码; 度分布; 非规则重复累积码; 差分进化
1962年,Gallager在其论文中首先提出了LDPC码(Low-Density Parity-Check Codes)[1],但当时并未受到重视,直到上世纪末被Mackay重新发现后,才掀起了一股研究与应用的热潮。LDPC码是一类由非常稀疏的奇偶校验矩阵及Tanner图定义的线性分组前向纠错码,它具有简单的结构描述与硬件复杂度,可实现完全并行操作,有利于高速、大吞吐能力译码,译码复杂度亦比Turbo码低,且具有更优良的基底(Floor)残余误码性能,因此,LDPC在现代通信系统中得到了越来越多的应用。常用的非规则LDPC码校验矩阵的非系统比特部分为双对角线结构,即IRA码(Irregular Repeat-Accumulate codes),这种结构的特点给度分布优化设计增加了更多约束。本文研究的重点是分析IRA码构造方法,从中提取码构造的特定约束,并转化为度分布序列中各分量的相关性描述,以便消除相关性,利用差分进化DE(Differential Evolution)搜索最优化的度分布序列,同时提出了改进方法,在一定程度上加快了搜索速度和性能。
1 IRA码的构造
1.1 度分布序列的定义
设LDPC码的码长为n,信息比特长度为k,校验比特长度为m,则n=k+m,码率R=k/n。λ(x):=Σλi xi-1代表非规则LDPC码Tanner图中变量节点(v-node)的度分布,ρ(x):=Σλi xi-1代表校验节点(c-node)的度分布。这里,λi是度为i的变量节点连接的边占Tanner图中所有边的比例,λi是度为i的校验节点连接的边占Tanner图中所有边的比例,最大的变量节点度为dv,最大的校验节点度为dc。非规则LDPC码度分布序列可表示为λ2λ3…λdv, ρ2 ρ3…ρdv),容易验证下列等式:

定义Nv(i)为度等于i的变量节点个数,Nc(i)为度等于i的校验节点个数,推导得出:
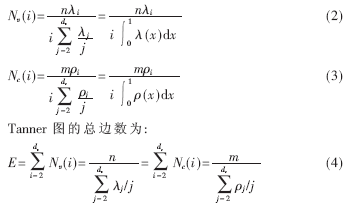
1.2 IRA码构造法
下面分析参数文献[3]中IRA码的构造方法。构造一个(n-1,k)非规则LDPC码,其校验矩阵为:

其中,H1是受度分布约束、随机产生的稀疏矩阵,且不含重量为2的列;T包含了H中所有重量为2的列(即度为2的变量节点)。
在矩阵T最后添加度为1的列构成H2,产生一个新矩阵H,作为IRA码的校验矩阵,如式(6)、(7)所示[3]:
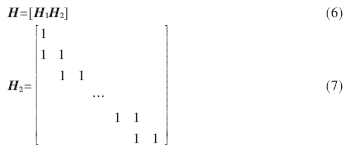
在校验矩阵中添加度为1的列后,IRA码度分布只有略微变化,且该列位于校验比特位置,对BP(Belief-Propagation)迭代解码后的误码率影响很小。从构造方法可知,IRA码度分布受如下特殊约束:
约束:所有度为2的变量节点都分配给奇偶校验比特,且度为2的变量节点个数刚好为m(包括度为1的列)。m为IRA码的校验比特长度。
通过推导,由(6)式得系统码生成矩阵:

式中H2T为上三角矩阵,可用传递函数为1/1+D的差分编码器实现,因此,IRA码很容易在硬件上实现快速编码。
对于已知码率为R的IRA码设计,设计约束实际上规定了度为2的变量节点个数和位置,结合(4)式,有:
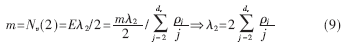
又根据(1)式,有:


从一个dv+dc-6维各分量不相关的分布矢量(λ4…λdv-1, ρ2…ρdc-1),可依据(9)~(12)式依次计算ρdv、λ2、λ3和λdv,从而唯一确定度分布序列。
2 密度进化的高斯近似和度分布优化
密度进化理论是分析度分布序列噪声门限值的强有力工具,然而该理论涉及很多卷积运算,运算量大。为了简化计算,Sac-Young Chung等针对加性高斯白噪声信道AWGN(Additive White Gaussian Noise channel)提出了密度进化的高斯近似分析方法。在消息独立和消息密度高斯分布条件下,该方法仅分析消息密度高斯分布均值,极大地减少了计算量。这里列出高斯近似分析法的消息密度均值递推公式:
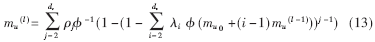

使用(13)式计算消息概率密度函数,从而得到迭代后解码误比特率,若误比特率小于预设值ε(如10e-6),则适当增大σn2,直到误比特率大于ε。经尝试,求得度分布(λ,ρ)在误比特率小于ε时的最大σn2,确定为该度分布的噪声门限。
3 DE方法及改进
DE是一种并行搜索方法,能够搜索连续空间非线性代价方程的全局极值。该方法有能力使搜索跳出局部极值点,避免错误的收敛。DE的特点在于产生测试参数矢量的方案。以DE实现IRA码度分布序列优化的步骤如下,流程如图 1所示。

(1) 初始化:确定度分布序列中参与DE的变量个数L,随机产生Np个L维随机矢量xi,g(0≤i≤Np-1,g为迭代次数);
(2) 计算门限f(xi,g),找出最大值,设门限最大的矢量为基本矢量xb,g(如图中xb,g=xl,g);
(3) 对于每一个矢量xi,g,在其他矢量中随机选择两个矢量xr1,g和xr2,g,定义F为权重因子,以下式计算新矢量vi,g,vi=xb,g+F(xr1,g-xr2,g);
(4) 新矢量ui,g的每个分量以概率CR取vi,g的对应分量值,以概率(1-CR)取xi,g的对应分量值;
(5) 选择:如果 f(ui,g)> f(xi,g)则xi,g+1=ui,g否则xi,g+1= xi,g;
(6) 停止准则:如果超过了最大迭代次数或所有矢量已经充分接近,则迭代结束;否则跳转到第(2)步。
权重因子F对DE的影响很大,增大F会加快收敛速度,但容易收敛于局部极值点;减小F则效果相反。这里,F取0.8;测试矢量数Np取10L~30L;交叠参数CR对DE的影响比F小,它更像一种微调,取较大的CR会加快收敛速度,一般在[0.5,1]中取值。
使用DE搜索IRA码的最优度分布序列,首先要消除度分布序列各分量的相关性,否则搜索到的结果无法满足IRA码设计的特定要求。1.2节最后指出dv+dc-6维的分布矢量(λ4…λdv-1, ρ2…ρdv-1)中各分量消除了相关性,并唯一确定度分布序列,因此,笔者在优化中使用该矢量。
DE搜索IRA码的最优度分布序列相当耗时,特别是当dv和dc较大,即测试矢量维数较大时,差分进化的速度很难让人满意,根据一些先验知识和测试结果,在不影响最终结果的前提下,改进了DE方法,加快了优化速度。
测试表明,DE的大部分时间消耗于第二步的门限计算上,因而,改进的主要目标是减少门限计算的时间,为此首先要减少DE测试矢量维数。
先假定在IRA码的度分布序列中只有(λ2λ3λ4λdv, ρdv-1 ρdv)大于零,其他都为零,根据(9)~(12)式,去相关性之后的矢量为(λ4,ρdv-1),矢量维数从dv+dc-6维锐减为2维。实验结果表明,矢量每减少一维,DE的收敛时间大约减少一半,改进后DE可迅速收敛。我们称这种维数削减的DE过程为“DE_FIRST”。一般来说,在dv不大时(如dv<10)结果已经很接近最优的度分布了,但当dv较大时结果距最优的度分布仍有一定差距,这时还要搜索更优的度分布。适当调整当前的最优矢量(λ2λ3λ4λdv, ρdv-1 ρdv),在该矢量的一定范围内随机产生L=dv-2个矢量,并在此约束下随机产生若干取值较小的矢量(λ5λ6…λdv,ρdv-2)组成dv-2维随机矢量(λ4…λdv-1, ρdc-2, ρdc-1),然后从DE的第二步开始继续搜索。这里并没有扩展(ρ2…ρdc-3)是因为将这些分量设为零几乎不会影响优化度分布的结果。扩展后的随机矢量唯一确定的度分布已经十分接近最优化的度分布了,所以DE的收敛速度比一开始就随机产生dv-2维随机矢量的DE快很多。我们称维数扩展以后的差分进化过程为“DE_SECOND”。
通过分析大量优化结果和其他文献给出的优化序列可以发现,λ4数值较小,大多取值在[0,0.2]内,ρdc-1也比ρdc小,一般取值在[0,0.4]。这样,“DE_FIRST”的初始随机矢量选择范围可以减小,在第一步中,矢量(λ4,ρdc-1)的两个分量分别在上述两个区间随机产生。实验证明,这样做能够加快搜索速度。
4 仿真结果
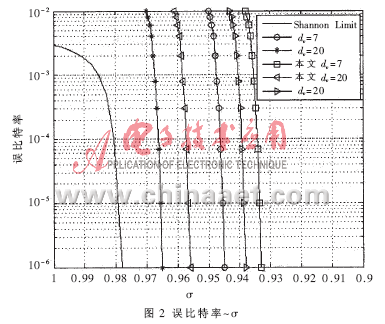
仿真参数设置如下:码率为1/2;差分进化的Np=20L,F=0.8,CR=0.8。表1列出了用本文介绍的基于密度进化高斯近似的DE搜索方法得到的最优化度分布,同时还列出了参考文献[4]优化得到的非规则LDPC码度分布和参考文献[5]同样用密度进化高斯近似优化得到的非规则LDPC码度分布。最后一行是度分布对应的噪声门限。比较dv=20的噪声门限可知,本文方法得到的最优化度分布优于参考文献[5]中的最优化度分布,如图2所示。由于优化后的非规则LDPC码的Nv(2)一般略大于(11)式规定的值,因此在约束下搜索的IRA码度分布中λ2比优化的非规则LDPC码度分布中λ2小,如表1所示。若没有IRA码的设计约束,本文介绍的方法可以搜索到更好的度分布序列。表2是DE改进前后收敛时间及噪声门限?滓的对比(仿真程序运行于1.5GHz PC机),可知,改进前后优化的度分布噪声门限很接近,而改进方法能够节省大约30%的搜索时间。


本文通过分析IRA码构造方法的特定约束,消除了度分布序列各分量之间的相关性,从而利用DE方法搜索具有更高噪声门限的度分布序列,并利用先验知识改进了DE方法,加快了搜索速度。这种方法也可以用来搜索其他构造方式下优化的度分布序列,对更广泛的非规则LDPC码优化设计具有一定的借鉴意义。
参考文献
[1] GALLAGER R G. Low-density parity-check codes[J].IEEE Trans. Inform. Theory, August, 1962:21-28.
[2] JIN H, KHANDEKAR A, MCELIECE R. Irregular repeataccumulate codes[J]. in Proc. 2nd. Int. Symp. Turbo Codes and Related Topics, Brest,France, Sept. 2000:1-8.
[3] YANG M, RYAN W E, LI Y. Design of efficiently encodable moderate-length high-rate irregular LDPC
codes[J]. IEEE Trans. Commun, 2004,52:564-571.
[4] RICHARDSON T, SHOKROLLAHI A, URBANKE R. Design of capacity-approaching irregular low-density paritycheck codes[J]. IEEE Trans. Inform.Theory, 2001,47(2):619-637.
[5] 肖娟,王琳,邓礼钊. 不规则LDPC码的密度进化方法及门限值确定[J]. 电子与信息学报, 2005,27(4):617-620.

