摘  要: 用模糊控制方法对单路口多相位的交通信号进行控制,提出以当前相的主队列和后继相的主队列决定信号配时的方法,并用Matlab及其模糊逻辑工具箱实现二维模糊控制器。以通过交叉口的平均车辆延误作为评价指标,衡量该控制器的控制性能,采用Matlab编程设计实现了交叉口六相位的仿真系统,仿真结果表明控制效果比较好。 

    关键词: 单路口交通  多相位  模糊控制  仿真  MATLAB

    单路口交通控制就是确定交叉路口红绿灯的信号配时,使通过交叉口的车辆延误尽可能小。传统的控制一般是采用模型控制或预先人为地设定多套方案,实践表明这种方法的控制效果并不理想。由于道路上的交通流具有较大的随机性和相当的复杂性,所实施的相位控制也应随交通流的不同而相应变化。近年来用模糊控制方法实现交通系统的控制,得到国内外学者的关注^[1～3],但同时考虑多相位和倒计时问题的研究并不多见。本文提出根据当前相和后继相的车辆等待长度确定单路口多相位信号配时的方法。该模糊控制方法可用于安装倒计时器的路口,具有良好的实用性。 

    MATLAB是国际上流行的控制系统计算机辅助设计语言和软件工具,其提供的模糊逻辑工具箱拓展了MATLAB对模糊逻辑系统的设计能力,已经成为运用模糊手段解决工程问题的有力工具。笔者用MATLAB软件并结合其模糊逻辑工具箱,实现了该模糊控制器及其仿真。计算机仿真结果表明控制效果优于定时控制。 

1 交通信号模糊控制思想 

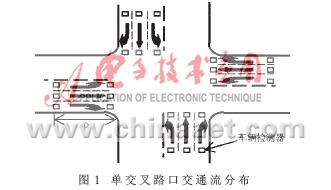
    单交叉路口交通流分布如图1所示。东、南、西、北四个方向,每个方向均有右行、直行和左行三个车道车流。在每条入口道上设置两个信号检测器构成一个检测区,一个设在停车线处,用于检测该道的车辆离开数;一个设在距第一个检测器D处,用于检测车辆到达数。距离D一般为80～100m。检测器对路口各个车道车流量进行实时检测而获取车流量信息,为模糊控制提供必要的数据。 

    下面以图2所示的单交叉路口6相位信号控制为例介绍模糊控制策略。 

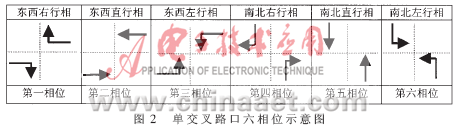
    令q_jk表示第j相位对应的两个方向的车辆等待队列长度(下称队长),j=1,2,3,4,5,6,为相位序号,k=1, 2,q_jk∈[0,Q_limit], Q_limit=D/L,L为单位车身长度。考虑某个周期T,在T内第i相位末时(第i相将由绿转红)任一车辆等待队列长度设为q_jk(i),则: 

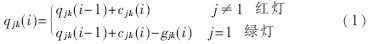
式中q_jk(i-1)为周期T内第(i-1)相位末时jk车道的车辆等待队列长度。c_jk(i)为第i相位jk车道的车辆到达数,g_jk(i)是第i相位从红灯变为绿灯后的车流离去数。 

    依据各个车道的车流信息,以路口流通能力最大或排队候车的时间最短为目标,对交叉路口交通信号进行模糊控制,实时确定各个相位的配时,因而周期和绿信比是不定的。设e_i(i=1,2,3,4,5,6)是第i相位的绿灯配时,它由路口实时检测的车流量决定。具体地说,每一相交通信号的配时是由该相位的主队列和后继相的主队列两者决定的。所谓主队列是一个相位两个方向中车辆等待数较大的等待队列,又称关键车流^[3]。 

2 模糊控制器的设计及模糊响应表的构造 

    所谓模糊控制就是在控制方法上应用模糊集合论,运用模糊语言变量及模糊逻辑推理实现系统的智能控制。这种方法摆脱了对控制对象输入、输出物理量的精确描述,用自然语言描述专家控制策略,以机器模拟人的模糊思维对系统实现有效控制。模糊控制系统原理如图3所示^[4]。

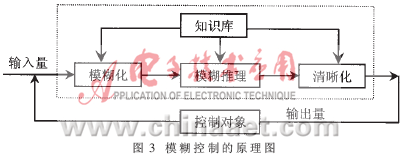
    在实际控制过程中,将计算机采样的输入量(精确量)模糊化,经模糊推理确定控制量的模糊值,最后进行反模糊处理获得控制量的实际输出,对被控对象进行控制。 

2.1 确定模糊控制器的输入输出变量 

    根据前文所述,单路口交通的多相位模糊控制器是一个二维模糊控制器。其输入是当前相的主队列q_p和后继相的主队列q_s,输出是绿灯时长相对于设定配时m的增量△e。q_p和q_s有以下三种组合:(右行,直行)、(直行,左行)、(左行,右行),分别对应右行相、直行相、左行相的控制。以直行相为例讨论控制器的设计,其它相位的控制与此相似,不复赘述。 

    设q_p是直行主队列长,q_s是左行主队列长。直行队长基本论域为[0,Q_limit],设其论域为Q,Q={0,1,2,3,4,5,6,7,8,9,10}。在论域Q上定义的五个模糊子集为{很短,短,中,长,很长},简记为{VS,S,M,L,VL}。直行队长的隶属函数定义见图4。从基本论域到论域的线性变换公式为: 

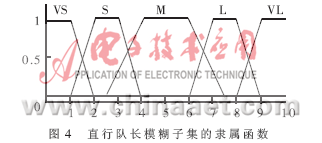
    左行队长q_s基本论域为[0,Q_limit],设其论域为S,S={0,1,2,3,4,5,6,7,8,9,10}。在论域上亦定义五个模糊子集{VS,S,M,L,VL},各模糊子集的隶属函数见图5。从基本论域到论域的线性变换同公式(2)。 

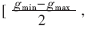
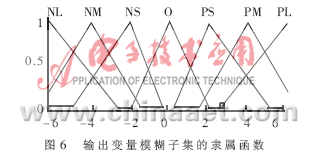
    绿灯时长e∈[g_min,g_max],设定配时m可取,控制器的输出△e=e-m,其实际变化范围为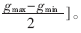设其论域为E,为便于选取变量的词集,定义E={-6,-5,-4,…,4,5,6}。在E上定义的七个模糊子集为{负大, 负中, 负小,零, 正小, 正中, 正大},记为{NL,NM,NS,O,PS,PM,PL}。图6是输出变量各模糊子集的隶属函数。 

2.2 确定模糊控制规则 

    确定控制规则的原则是:当等待队列长或很长时,增加绿灯时间,选取的输出以放行、减少车辆等待为主;而当等待队列较短时,选取的控制量以防止绿灯时间浪费为出发点。通过总结实践和专家经验,建立了模糊控制规则表,如表1所示。一共有5×5=25条控制规则。 

    双输入单输出的模糊控制器,其控制规则可写成如下形式: 

    if (q_p is Q_i) and (q_s is S_j) then (△e is E_ij) 。 

    这里Q_i,S_j,E_ij分别是上文定义的模糊语言变量。根据每一条规则,都可以求出相应的模糊关系R_ij: 

    R_ij=Q_i×S_j×E_ij     (i=1,Λ,5)                      (3) 

    所有控制规则对应的模糊关系为R,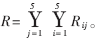 

2.3 模糊推理及反模糊化的方法 

    根据模糊推理合成规则运算,得出相应的控制量变化的模糊集E,E=(Q×S)oR,即: 

    “o”是合成运算符。合成的结果是一个模糊子集,可按隶属度最大法、中位方法或加权平均法进行反模糊化,得到在区间E上的精确控制量△e^*,再经尺度变换后得实际的控制量增量△e。设直行相绿灯实际范围为[g_min,g_max],右行、左行相绿灯实际范围为[g′_min,g′_max],可按下列公式转换为实际控制量e: 

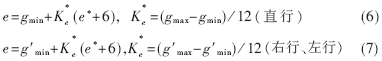
    式中,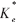为由论域到基本论域的比例因子。直行相和右行相、左行相使用的比例因子不同。 

2.4 模糊响应表的生成 

    根据输入和输出变量的隶属函数、模糊控制规则,由模糊逻辑运算可离线算出模糊关系矩阵R。R庞大,不利于储存和在线运算,通常应进一步求出模糊响应表,即模糊控制表。在实际控制过程中,可根据模糊量化后的输入变量值,直接查询模糊响应表,以获得控制量的变化值△e^*。再运用(6)或(7)式,得到绿灯配时,去控制信号灯和倒计时器。 

    下面以直行相为例给出生成多相位模糊响应表的函数,straight.fis是直行相模糊控制器。 

    function ulist=anstable() 

    sfis=readfis(‘straight’);    %打开straight.fis,并加载到当前工作空间 

    ulist=zeros(11,11)             %ulist 是模糊响应表 

    for i=1:11 

      for j=1:11 

        qp=j-1;ps=i-1; 

        ulist(i,j)=evalfis([qp,qs],sfis)%执行模糊推理运算 

    end 

    end 

3 仿真系统设计与实现 

3.1 评价指标计算 

    本文以通过交叉口的平均车辆延误作为评价指标,以此衡量多相位模糊控制器的控制性能。设在一个周期T内,第i相位jk车道的车辆延误为d_jk(i),则: 

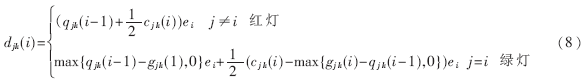
    所以,第i相位所有进口的车辆总延误为: 

    同理,设在一个周期T内所有进口车辆到达数为C(T),则: 

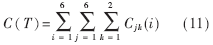
    所以k个周期内六个进口的车辆平均延误为:   

    其中,Q₀为周期开始时所有进口的初始队列长度之和,即在第一个周期开始时,车辆等待队长之和。 

3.2 仿真系统设计与实现 

    设T为周期,i为相位,单路口多相位模糊控制器的仿真系统流程图如图7所示。 

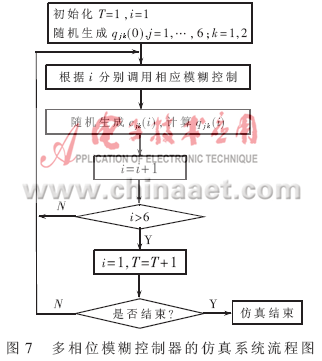
3.3  仿真结果分析 

    笔者用MATALAB 5.3 编写了单路口交通的多相位实时模糊控制仿真程序,仿真参数Q_limit=20,[g_min,g_max] 取[20,60],[g′_min,g′_max]取[10,20]。作为对比,亦编写了定时控制方法仿真程序,直行相位取60秒,其它相位取20秒。为保证结论的可靠性,将模糊控制与定时方案作了多次仿真比较,每次仿真为10个周期,结果见表2。

    经过多次仿真运行,得到模糊控制车辆平均延误d1=131.95秒/辆,定时控制方法的车辆平均延误为d2=141.91秒/辆。模糊控制方法的车辆平均延误与定时控制方法相比,减少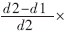100%=7.02%。可见,采用模糊控制方法,绿灯时间随交通量而变,车辆平均延误减少,因此比定时信号更能适应交通量的随机变化,通行能力增大。 

    多相位模糊控制器适用于单路口多车道的交通控制。由于每一相位的配时是根据路口实时数据经模糊推理一次确定,可用于安装倒计时器的路口,仿真结果表明该方法是有效的。 

    如果不借助于开发工具,用高级语言如C语言或汇编语言等自行编程设计模糊控制器,则开发时间长、效率低且通用性差。笔者用MATLAB提供的模糊逻辑工具箱[5]辅助设计多相位模糊控制器,方便快速,大大缩减了编程工作量,且论域、语言变量、隶属函数、控制规则等设定和修改非常容易。对于参数不确定系统,更便于分析不同参数对控制结果的影响,以寻找更优的控制效果。 

    改善模糊控制性能的最有效方法是优化模糊控制规则。通常,模糊控制规则是通过将人的操作经验转化为模糊语言形式获取,带有相当的主观性。运用粗集理论、遗传算法优化规则,是笔者进一步的研究内容。 

参考文献 

1 Mohamed B.Trabia, Mohamed S.Kaseko, Marali Ande.A Two-stage Fuzzy Logic Controller for Traffic Signals.Transportation Research Part C 7,1999: 353～369 

2 陈 洪,陈森发.单路口交通实时模糊控制的一种方法.信息与控制,1997; 26(3): 227～233 

3 陈森发,陈 洪,徐吉谦.城市单路口交通的两极模糊控制及其仿真.系统仿真学报,1998;10(2):35～40 

4 李士勇.模糊控制·神经控制和智能控制论. 哈尔滨:哈尔滨工业大学出版社,1996:250～387 

5 黄文梅,杨 勇,熊桂林.系统分析与仿真-MATLAB语言及应用.长沙:国防科技大学出版社,1999:190～201