摘  要: 针对传统的“高频用测频法,低频用测周法”的频率测量的精度差异过大的不足,提出了在高低频实现等精度测量的周期滑动扩展的测周法,并在单片机上予以实现。 

    关键词: 频率测量  等精度测量  周期滑动扩展  单片机

    长期以来,在频率测量领域内一直沿用着“高频用测频法,低频用测周法”的方法,这种做法对提高测量精度无疑是十分有效的,但却存在两个问题:一是被测频率越高或被测频率越低则测量精度越高,但不同频率下的测量精度差异甚大;二是在测频法和测周法的频率衔接点附近不可避免地存在着测量精度的跳变,使同一频率的各次测量结果不同。这两种测量的精度离散性问题大大降低了测量结果的置信度,尤其在很多以频率为判据的诊断系统中更是如此。这时人们往往希望在整个频率测量域中能获得精度一致的测量结果,然而在经典的测频和测周法中,却难以解决甚至无法解决。为此,本文摒弃了传统的测频与测周相结合的方法,采用单一测周法并辅以周期滑动扩展算法,在单片机上实现了高频到低频范围内的等精度测量,从根本上解决了测频与测周结合方法的不足。 

1 周期滑动扩展的测周法 

    在周期测量法中,顾名思义是要测出被测信号两相邻脉冲间的间隔时间,如图1所示。 

    由图1可知: 

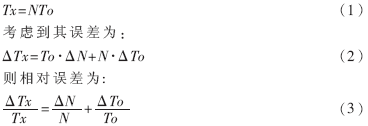
    (3)式中第二项实际上是系统的时基误差,通常取决于系统的晶振频率稳定度,与被测频率无关,而且因其值在10^-6～10^-9/d之间,所以在所要求的相对误差未接近该范围时可认为: 

    又由于量化误差ΔN=±1(在本系统中实际上ΔN≤1),所以有: 

    由(5)式可见,计时次数N的大小基本决定了相对误差的大小,显然,N越大越好。 

    由(1)式可知: 

    (6)式中To由系统时钟确定,无法改变;而Tx则随被测Fx而变。显然要增大N,就必须增大Tx,在Tx无法随意改变的情况下可考虑采用周期扩展法变通解决。 

    令: 

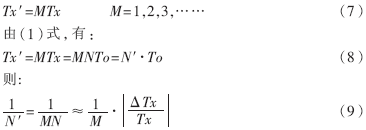
    即多测M个Tx周期后,计时次数N′也随之扩大M倍,必然使相对误差缩小为原来的1/M。显然对不同的Fx,只要选取合适的M,便能满足所要求的相对误差,进而实现被测频域内的等精度测量。由于M是由被测频率Fx而定,因而这种周期扩展是可灵活滑动的。 

    值得说明的是,当被测频率很低时(例如Fx=0.01),即使选M=1,也可能使测得的N很大。此时已无法考虑Fx较高时的等精度问题,好在此时精度是上升而不是下降的。 

2 测量周期滑动扩展的硬件配合 

    在同样的精度下,周期滑动扩展的测周法对时基频率和硬件电路的要求比经典的测频与测周相结合的方法低得多,因而很适于在单片机上实现。但在具体实现时还应考虑相应的硬件配合,即周期扩展因子M应当分为两部分,其中一部分由单片机片内解决,另一部分则应由片外硬件解决。 

    M由单片机片内解决很好理解,只要根据预测所得的N和精度所要求的N′求出相应的M,由软件控制测量M个Tx周期即可。M之所以还要由片外硬件解决一部分,是考虑到当Fx很高时,其受单片机内置计数器硬件的计数频率所限而无法对片外脉冲进行计数。具体说来,当89C51采用12MHz晶振时,由于其T0引脚识别外部一个脉冲需要两个机器周期,所以其片内计数器的上限计数频率仅为500kHz。若被测Fx大于此值则无法直接测量其Tx。解决的办法是将扩展因子M的一部分由外部硬件分频器承担,分频器级数的切换由单片机控制,这样便可由单片机外部实现部分的周期扩展。笔者实现此功能时分频器采用8级,如图2所示。这样当Fxmax=100MHz时,外部分频器由单片机切换为8级,则Fxmax经8级分频后送到单片机计数端的Fx′仅为100MHz÷2⁸=390.625kHz,完全满足计数器硬件的要求。显然若想进一步提高测量频率的上限,只要相应增加片外分频器的级数即可(当然还得考虑印制版排版、测量电路前级以及测量探头的高频设计问题)。 

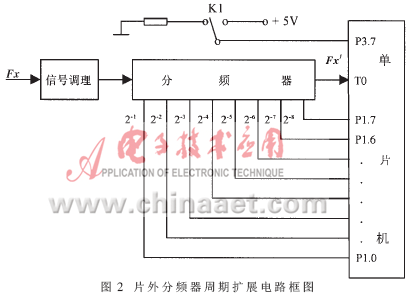
    此外在具体实现时还得注意合理选择片外分频器电路的速度。显然第一级要求最高,宜选传输速度在6.5ns的SN74F74(双D)。这样在Fxmax=100MHz时,两级下来频率便降为25MHz,后级便可选常规电路了。 

    由图2还可看到,Fx′送到单片机的计数端T0。按理说,测周期只要能测到信号的跳变即可,那么单片机的大部分引脚均可实现这一点。这里之所以选T0,是基于其具有2¹～2ⁿ的计数功能。当测一个周期时,利用其装入2ⁿ-1后计入一个脉冲便能溢出的特点连做两次即可;当测k个周期时,装入2ⁿ-k后一次计数溢出便可完成,不仅十分方便,而且省去了k次溢出中断服务中应做的软件工作和由此带来的时间延误和测量误差。从这个意义上说,T0引脚对应的片内计数器TC0以硬件方式承担了拟由单片机软件实现的周期扩展任务。由此可以进一步认为,此处的周期滑动扩展实质上是由单片机片内外两部分硬件分频器在软件的控制下协调完成的。 

3 周期扩展因子的配置与调整 

    由于周期扩展因子M系由片外M1与片内M2两部分组成,且两者作用不尽相同,因此配置与调整时要有所区别。其中M1控制的分频器承担着单片机计数端T0能否正确识别高频时Fx′的重任。因此配置与调整时应当优先考虑M1。同时考虑到在测量开始时无法预计被测频率的高低,因此M1的初始值应设置为其配置的最大值2⁸。至于M2,由于其处于周期扩展的第二级,因此在第一级级数确定的前提下,M2的最大值决定了测频范围的上限。现因本系统设定的最高测量频率为100MHz,所要求的相对误差为10^-4,系统的晶振频率为12MHz,因此由(9)式可知计时值N′必须不小于10⁴,所以在Fxmax=100MHz的情况下,由(8)式可得: 

    因2²⁰=1024·1024>10⁶,所以取Mmax=2²⁰,前已确定M1max=2⁸,由此得:M2max=2¹²。为了在实际处理时方便起见,分别取其指数为实际调整值:m1=0～8,m2=0～12。 

4 周期滑动扩展等精度测频的软件实现 

    如前所述,要实现周期滑动扩展的等精度测频,只要根据测量的中间结果动态地调整周期扩展因子m1或m2即可。具体说来就是当测量所得的计时值小时增大m1或m2,反之则减小,但在软件实现时还得处理量程换档和超量程判断等问题。 

    量程换档可分为自动和手动两种方式。手动换档是在测量时由人工按键告诉系统Fx处在什么范围,自动方式则完全不需人工干预。本系统没有必要完全采用手动方法,这是因为周期滑动扩展的算法本身便具有一定的自动换档作用。然而也难以完全采用自动方式,因每次测量时由于无法预计Fx是处在高端还是低端,因而难以确定两个扩展因子的初值。例如,Fx大于500kHz时,不接入片外8级分频器T0端便无法识别Fx的输入脉冲;但当Fx很低例如为1Hz时,片外8级分频器的接入将使原本只需1秒的测量过程竟然长达256秒。为此在片外增加一个选择开关K1,由其读入的电平决定片外8级分频器是否接入。显然K1的状态取决于Fx是否大于等于500kHz。 

    超量程的判断只能通过测量的结果来下结论。本系统的测量范围为100MHz～0.001Hz。由前面所述的系统参数不难得出,在高端当Fx>104.8576MHz时,系统的计时次数将小于10⁴,由此便可下“Fx超上限”的结论,当然这里给Fxmax留了约4%的余量。在低端当Fx<0.0009313Hz时,系统的计时次数将大于10⁹(超过30位二进制),由此同样可下“Fx超下限”的结论,当然这里也给Fxmin留了约6.9%的余量。 

    解决以上几个主要问题后,便可在软硬件的适当配合下以周期滑动扩展的测周法实现高低频的等精度测量。图3给出了相应的测量主流程图。 

    由图3可见,周期测量的计时始于T0端测得的第一个脉冲的下跳沿,它利用了TC0在装入2ⁿ-1后计入一个脉冲便会溢出,以及相邻两个机器周期测得一高一低便会计数的特点。这种以硬件进行的检测要比软件指令做得可靠和干脆得多,因为89C51的检测指令最快也要2个机器周期(12MHz晶振时需2μs),而T0端输入500kHz时稍有延误便会造成检测失误(例如其它指令或中断服务)。并且这种硬件检测法不会影响紧随的后续脉冲的正常识别,因为在高频时,后续的测量会自动增加片外分频器的级数m1,在低频时则后续脉冲相隔甚远。周期测量计时的停止则是由m2给TC0赋值后计得2^m2个脉冲周期时的溢出来实现的。 

    由图3的算法和上述系统参数还不难得出,在Fx=100MHz～100Hz的频率范围内,测量的响应时间为21ms～33ms。Fx=10Hz时,响应时间为100ms。以后便随Fx的下降,其响应时间也相应增加。显然这是受被测频率自身的限制,与算法无关。由此不难看到,这种算法的另一优点是在大部分测量频率范围内其测量响应时间十分接近。当然若想进一步加快的话,只要将上述流程中m1与m2的递增递减循环改为查表即可。此外,测量响应时间还与系统要求的测量精度有关。精度要求越高,则测量所需时间越长。 

    最后在软件中还得注意主程序与各中断服务程序的时间配合。以及运算程序的字长与精度等问题,限于篇幅此处不再赘述。 

    本文介绍的周期滑动扩展的测周法以测量精度为准绳,灵活调整被测信号的周期数,使其能在大部分测量频域内实现等精度测量,同时也使测量时间的差异大为减少。由于这种方法是用增加测量周期来提高测量精度,因而比经典方法中提高计时晶振的频率来提高精度要方便得多,特别适合在单片机上实现。 

参考文献 

1 华南盾,朱 杰,张林欣.电子测量原理与模拟电路试验.上海:上海交通大学出版社,1993 

2 王永生.电子测量学.西安:西北工业大学出版社,1995 

3 杨吉祥,詹宏英,梅杓春.电子测量技术基础.南京:东南大学出版社,1999