数字语音混沌保密通信系统及硬件实现
2009-04-21
作者:唐秋玲 覃团发 姚海涛 林 硒
摘 要: 对离散时间动力学系统逻辑影射进行变换,使其在一定精度下产生数字混沌序列,采用该数字混沌序列作为密码,构造了语音保密通信系统,并运用单片机实现了该系统的硬件实验。
关键词: 数字混沌系统 语音加密 硬件实现
混沌系统具有对初条件极端敏感的特性,它可以提供大量非相关、类随机而又确定可再生的混沌序列。近几年来,研究混沌和应用混沌已经成为国际电子工业界前沿最活跃的一个研究热点,其中在保密通信方面的应用研究也越来越得到人们的重视[1-2]。
混沌序列在密码学方面的应用起源于80年代末期,由英国数学家Matthews首先提出[1],其后得到了一定的发展。国内南京大学声学研究所的倪皖荪、中国科学院的张洪均等也正在进行这方面的研究工作。
基于混沌系统之间能够达到自同步[2],发展了多种同步技术,如:混沌掩埋技术[3]、混沌调制技术[4]、混沌开关技术[5]以及数字混沌通信技术[6]等,分别运用于连续混沌通信系统和数字混沌通信系统。众所周知,数字通信系统以其抗干扰能力强,易于加密,易于大规模集成等特点,在通信行业中将取代模拟通信而占主要地位。而且,数字混沌系统比较模拟混沌系统具有结构简单,易于实现,保密性能高等优势。因而,混沌技术在数字保密通信中的应用研究也就更具有现实意义。
本文对离散时间动力学系统逻辑影射进行变换,使其在一定精度下产生数字混沌序列,采用该数字混沌序列作为密码,构造了语音保密通信系统,并运用单片机实现了该系统的硬件实验。
1 数字混沌序列的产生
研究证明逻辑映射
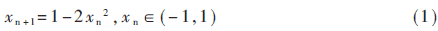
可以产生大量具有均值为零、自相关为δ函数、互相关为零统计特性的优良混沌序列,因而可作为理想的密码序列,应用于语音信号的保密传输。
要实现逻辑映射的数字化,一种方法是采用浮点运算。实际运算表明,浮点单精度(32bit)的运算结果脱离了混沌态,浮点双精度(64bit)的运算结果与理论接近。但在实际应用中,64bit浮点双精度运算需要内存空间大,运算速度慢,而且不利于数字硬件实现。下面我们把逻辑映射的迭代过程由浮点运算变换为定点运算。
我们日常生活中普遍使用的十进制小数同计算机中使用的二进制存在如下关系:
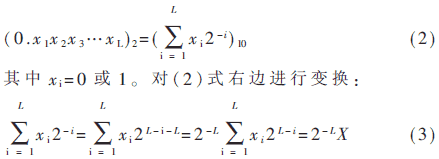
其中:,![]() 从(3)式可知,X为一十进制整数,它是由一个十进制小数映射而来,而十进制整数在计算机中可用定点整数形式来表示。
从(3)式可知,X为一十进制整数,它是由一个十进制小数映射而来,而十进制整数在计算机中可用定点整数形式来表示。
我们将(3)式代入逻辑映射(1)可得:

这就是逻辑映射的整数表达式。在作者即将发表的另一篇文章中,对L为64位、32位和16位分别进行了计算机编程模拟,证明当L=32时,式(5)产生的序列仍然处于混沌态(而同样32bit条件下,采用浮点运算得不到混沌序列)。当L=16时,式(5)产生的序列已经脱离了混沌态,但经过一定的非线性变换仍可产生混沌序列,对式(5)进行微小的改动(即非线性变换)为:
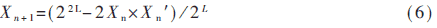
其中Xn=(XnH)(XnL),Xn′=(XnL) (XnH),即Xn′为Xn的高低字节互换后的16位二进制数。取L=16比特根据式(6)产生数字混沌序列的流程图如图1所示。因此整数运算优于浮点运算,它降低了对计算精度的要求。产生L比特输出,只需运算L×L比特定点运算,加快了计算速度,从而减低了对硬件电路的要求。
2 数字语音混沌通信系统
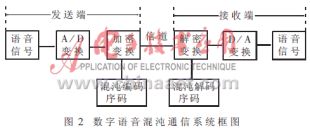
我们利用上述数字混沌序列作为密码构建了一个有混沌加密装置的语音数字通信系统(系统框图如图2)
发送端加密过程为:

其中Usn为发送端的语音信号,Xsn为发送端的混沌编码序列,Ysn为发送端的混沌加密信号,⊕为逐位模二加计算符。
接受端解密过程为加密过程的逆运算:

其中,Yrn为接收到的加密信号,Sn为信道的接收噪声,Urn为解密输出。显然,当通道噪声为零,收发双方采用相同的混沌系统(相同初条件的逻辑映射整数表达式(6))产生的编码序列进行加解密,即Sn=0,Xrn=Xsn时,就有Urn=Usn。从而实现误码率为零 的数字语音混沌保密通信。
3 硬件实现
我们运用单片机实现了上述数字语音混沌通信系统。单片微型计算机是微型计算机发展中的一个重要分支,它具有体积小、功能扩展性强、环境适应性强等独特结构和性能。用单片机实现数字语音混沌保密通信系统可以满足保密通信的隐蔽性、灵活性、保密性等要求。
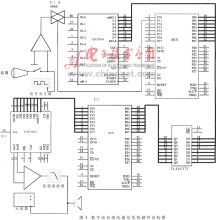
我们运用8031单片机设计的数字语音混沌通信系统硬件结构图如图3所示。在发送系统中,从话筒输入的语音信号经过4066芯片采样保持,根据人类语音的频谱成分一般在10kHz以下,而从一定可懂度考虑,只需保留3.5kHz以下的频谱,故采样频谱选取8kHz;在0809芯片进行数模转换;在8031芯片编程产生混沌密码序列,与输入的数字语音信号进行加密运算,然后把密文发送到通信线路上(采用基带通信)。接收端的单片机8031芯片用于接收密文信号并产生与发送端相同的混沌编码序列,然后两者进行解密运算并把解密信号输出到0832芯片;在0832芯片对解密信号进行数模转换变成语音模拟信号并经过放大和低通滤波后推动扬声器播放,整个通信过程为实时通信。从扬声器能够清晰的听到从发送端话筒输入的语音信号,但不可避免伴有一定的噪声,这是由量化误差和通道干扰引起的,其中主要原因是量化误差。为了说明该系统保密通信效果,在输入端,我们用信号发生器产生一1kHz方波信号输入该系统,并编写了两套程序。一套程序在发送端对方波信号加密但在接收端不解密。另一套程序在发送端对方波信号加密且在接收端解密,从示波器可观察到两种输出结果,加密信号的时间波形杂乱无章,完全覆盖了原始信号,从扬声器听到的是一片噪声。信号的加密、传输、解密过程产生的时延很小,不影响实时通信;解密后输出的方波信号与输入方波信号比较出现了一定的失真,但主要是高频失真,因而该系统成功的实现了语音保密通信。
4 讨论
在数字语音混沌通信系统的设计和实现中,数字混沌序列的产生是很重要的一个方面,它产生的方法直接影响到通信系统硬件的复杂程度。采用本文所述的由浮点运算变换到定点运算的逻辑运算的整数表达式来产生数字混沌序列,可以极大地加快计算速度,降低对计算精度的要求,因而可用广泛使用的8031单片机实现数字语音混沌通信系统。当然,要提高通信的效果,还要提高语音信号的采集速度,减少量化噪声,这就要求单片机具有较高CPU运行速度,可考虑使用高位单片机来实现该语音保密通信的硬件系统。同时,在选用高速CPU单片机的前提下,也可尝试利用上述语音数字通信系统对大数据量的图形、图象和多媒体信号实现保密通信或进一步改进系统为无线传输,以满足广泛的实际应用的要求。
参考文献
1 Matthews.On the derivation of a chaotic encryption an-gorithm.Cryptonogia,1989;(4):29~42
2 Pecora L M,Carroll T L.Synchronized chaotic signal and systems.IEEE ICASSP,in Proc.1992
3 Cuomo K M,Oppenheim A V.Strogatz S.H.Dynchronization of Lorenz-based chaotic circuits with applications to communications.IEEE Trans.on CAS,1993;CAS-40(10):626~633
4 Halle K S,Wu C W,Itoh M,et al.Spread spectrum communication through modulation of chaos.Int.J.Bifurca-tion & Chaos,1993;3(2):469~477
5 Dedieu H,Kennedy M P,Hasler M.Chaos shift keying:Modulation and demodulation of a chaotic carrier using self-synchronizing Chua's circuits.IEEE Trans.on CAS,1993,CAS-40(10):634~643
6 Frey D R. Chaotic digital encoding:An approach to secure communication.IEEE Trans.on CAS,1993;CAS-40(10):660~666