所谓图像分割" title="图像分割">图像分割就是指把图像分成各具特性的区域,并提取出感兴趣目标的技术和过程。它是数字图像处理中的关键技术之一,是进一步进行图像识别" title="图像识别">图像识别、分析和理解的基础。目前图像分割方面现有的算法非常多,将它们进行分类的方法也提出了不少。一般分为3类:(1)阈值分割;(2)边缘检测;(3)区域提取。但还没有一种方法能普遍适用于各种图像。因此,对于图像分割的研究还在不断深人之中,也是目前图像处理中研究的热点之一。随着科技的发展进步,图像处理在军事中的运用也越来越广泛,这主要集中在迷彩设计这方面。而现在军事上的伪装迷彩是现代高技术战争中隐藏武器装备、保存自我的重要手段,也是消灭敌人的需要。因此对于迷彩的设计研究也一直都是各国的热门话题。文中主要以某山地航拍图为研究对像,对其进行背景分析然后再实现图像分割,为后期迷彩设计做准备。由于该山地背景纹理特征明显,故利用纹理分析" title="纹理分析">纹理分析对其进行背景分析,而灰度共生矩阵" title="灰度共生矩阵">灰度共生矩阵是纹理分析方法中最常用的一种方法。文中采用灰度共生矩阵方法对该图像进行分割研究。
1 灰度共生矩阵
灰度共生矩阵(Gray Level Co-occurrence Ma-trix,GLCM)是图像纹理分析方法中的一种,它反映不同像素相对位置的空间信息,在一定程度上反映了纹理图像中各灰度级在空间上的分布特性,是纹理分析领域中最经常采用的特征之一。灰度共生矩阵是图像灰度变化的二阶统计度量,也是描述纹理结构性质特征的基本函数,它统计了两个像素点位置的联合概率分布。设S为目标区域R中具有特定空间联系的像素对的集合,则共生矩阵P可定义为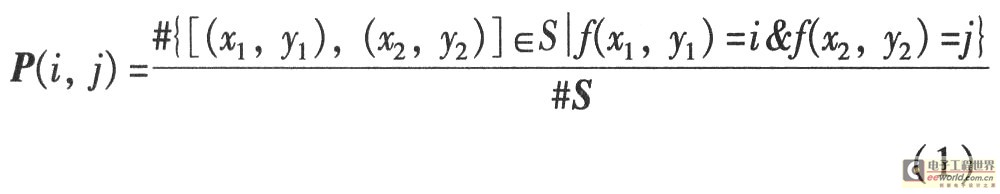
式(1)等号右边的分子是具有某种空间关系、灰度值分别为i,j的像素对的个数,分母为像素对的总和个数(#代表数量),这样得到的P是归一化的。
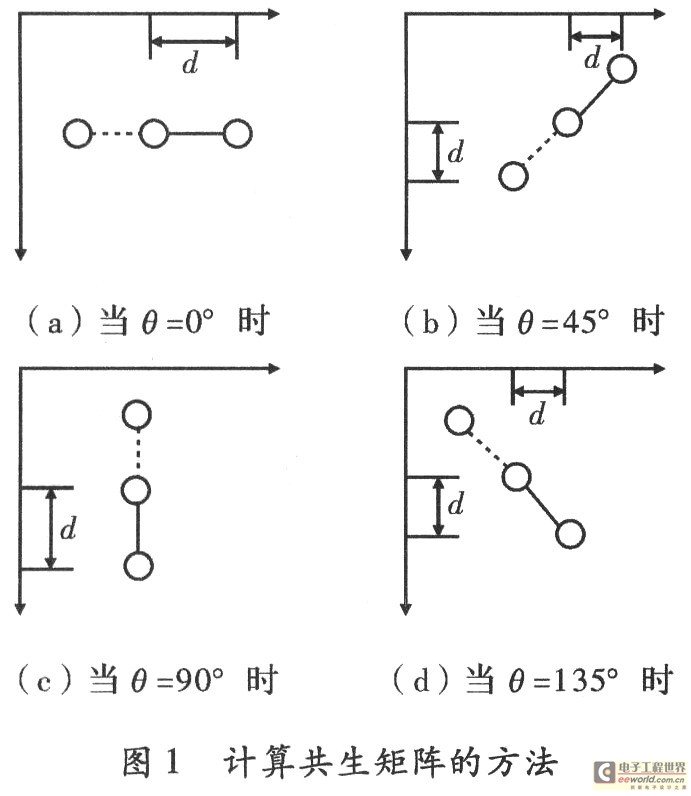
对于一幅图像Gf(i,j),大小N×N,包含像素(动态范围为G)的灰度级为{0,1,…,G-1},它的灰度共生矩阵是一个二维矩阵C(i,J),每个矩阵元素表示在某一距离d和角度θ强度i和j联合出现的概率。因此,根据不同的d和θ值,这里可能存在多个共生矩阵。但在实际应用中,往往适当的选取d,而θ一般取O°,45°,90°,135,如图1所示。
2 实验设计及分析
2.1 灰度共生矩阵的常用参量
实际应用中,作为图像纹理分析的特征量是由灰度共生矩阵计算出的一些参量。Haralick曾提出14种由灰度共生矩阵计算出的参量。但在本实验中主要用到的参量有以下4种:
(1)角二阶矩(Angular Second Moment,简记为ASM)。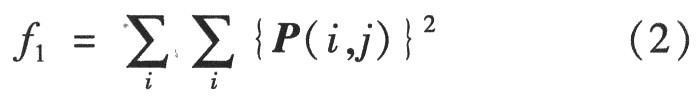
角二阶矩是灰度共生矩阵元素值的平方和,所以也称能量,反映了图像灰度分布均匀程度和纹理粗细度。如果共生矩阵的所有值均相等,则ASM值小;相反,如果其中一些值大而其它值小,则ASM值大。当共生矩阵中元素集中分布时,ASM值大。ASM值大表明一种较均一和规则变化的纹理模式;
(2)对比度(Contrast,简记为CON)。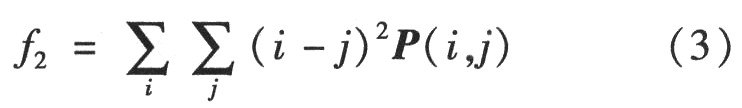
对比度反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的像素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,CON越大;
关键字:灰度共生矩阵 图像分割
(3)相关性(Correlation,简记为COR)。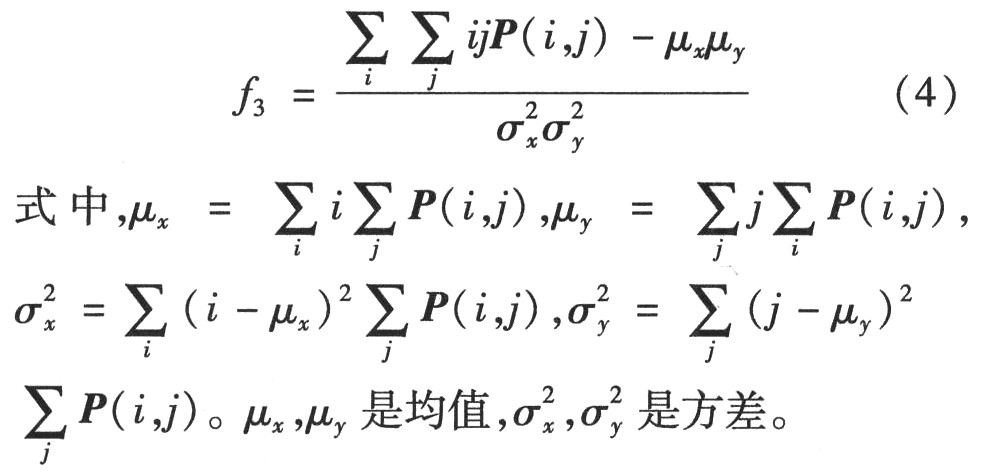
相关性可以度量空间灰度共生矩阵元素在行或列方向上的相似程度。因此,相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值就大;相反,如果矩阵像元值相差很大则相关值小。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值;
(4)熵(Entropy)。
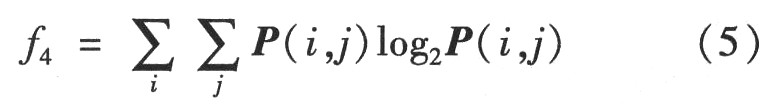
熵是图像所具有的信息量的度量,纹理信息也属于图像的信息。若图像没有任何纹理,则灰度共生矩阵几乎为零,则熵值接近为零;若图像充满着细纹理,P(i,j)的数值近似相等,则该图像的熵值最大;若图像中分布着较少的纹理,P(i,j)的数值差别较大,则该图像的熵值较小。
2.2 图像预处理
即对图像进行过滤,以便于提高图像识别的速度和准确率。图像预处理过程是对图像的一个过滤过程,要排除干扰,保留需要处理的部分,并过滤掉不需要的部分。以某山地照片为例,首先选取一定大小的图片作为研究对像,如图2(a)所示,然后将该图片扫描输入电脑,并对其进行编号。接着对其进行去除噪声和二值化处理,以便于更好的提取图像特征,如图2(b)所示。然而在计算共生矩阵时,由于计算量大,再将图像的灰度分成16个灰度级。

2.3 试验设计
关于纹理图像识别与分类的具体应用实例很多。一般的做法是通过纹理特征的度量方法对每张图像抽取一组纹理特征,由这些特征构成该样本的特征向量,然后在特征空间里应用统计模式识别方法对众多的图像样本进行识别与分类。在本实验中,样本图像经数字化处理后的像元数为109×116,将图像分成大小为16×16像素的非重叠窗口,共49个子图像,Ng=16(将0~255灰度分成16级)。每个小块都从4个方向(0°,45°,90°和135°)来提取特征,具体设计步骤如下:
(1)利用前述灰度共生矩阵计算出4个最主要的特征值(角二阶矩,对比度,相对性和熵值),然后取这4个方向的均值和方差表示该特征值,于是,4个方向值就变成2个。为此共可提供8个纹理特征值。将提取的特征值保存到纹理特征库中作为训练样本;
(2)计算出其他小块的纹理特征值作为未知样本,并对其进行编号;
(3)利用最小欧氏距离分类法将从未知样本中提取的特征值与纹理特征库中训练样本的特征值进行比对,当且仅当未知样本的特征向量与训练样本的欧氏加权距离最小时输出匹配成功的未知样本的编号,否则不输出。输出成功后将匹配成功的未知样本编号与训练样本编号进行统一调整;
(4)以另一未知样本的纹理特征值作为训练样本保存在纹理特征库中,利用上述类似方法进行模式匹配。重复步骤(2)和步骤(3),直至每个未知样本被输出。
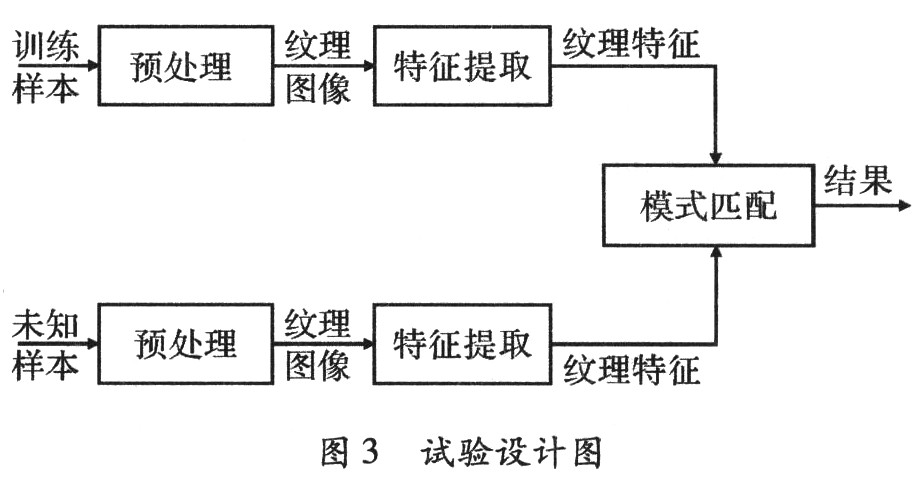
以上步骤全部运行完毕后,将得出相似纹理区域的小块具有相同编号,这样就实现了纹理分类,然后根据编号的不同实施区域整合划分,这样就可以实现纹理图像分割。具体实验设计过程,如图3所示。
关键字:灰度共生矩阵 图像分割
2.4 实验结果分析
根据前述步骤,利用Matlab和VC++工具对图像进行分析处理,然后利用聚类分析等方法实现的实验效果,如图4所示。
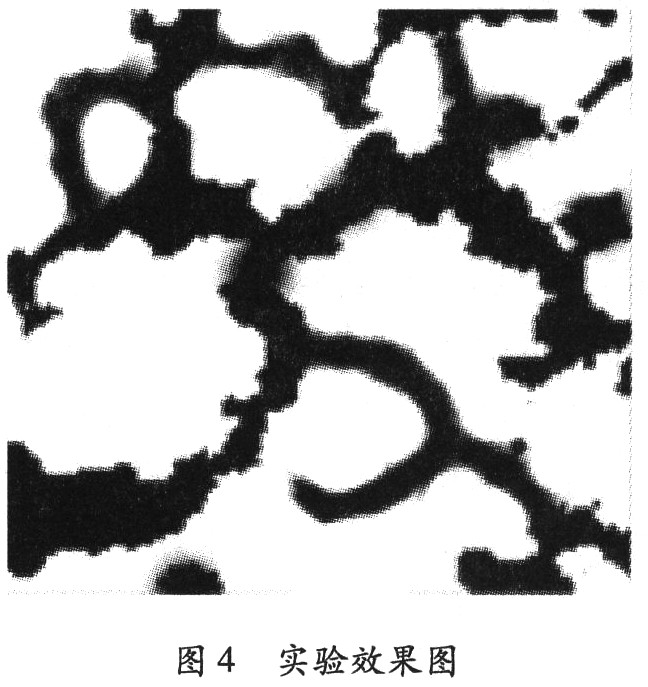
由图4可以看出,对于纹理特征明显的图像进行二值化后,再根据纹理特征值结合加权欧式距离进行图像特征处理,最终得到的效果图实现了较好的区域融合和划分,达到了图像分割的目的。
3 结束语
文中利用灰度共生矩阵方法对图像进行纹理特征提取,然后根据加权欧氏距离对每个纹理区域进行模式匹配,将图像按不同纹理区域进行整合划分。最后利用聚类等方法实现了图像分割。经过多次试验表明,对于具有显著纹理特征的图像,利用基于灰度共生矩阵的方法实现对图像的分割具有一定的准确性和实用性,并能较好的实现图像分割效果。

