摘 要: 用一种遗传算法的调度策略,以大维度矩阵求逆为实验对象,探索在多核中如何完成任务的均衡分配问题,以达到加速效果。算法利用系统资源的弹性,自动搜寻可以并行的子任务并将其合理地分配到相应计算节点中,提高了多核系统资源调度性能,实现了对用户提交的任务的优化调度,达到了均衡系统各处理器计算负载和提高多核系统的总体性能的目标。
关键词: 多核处理器;遗传算法;任务调度;矩阵求逆
随着多核系统硬件结构的成熟,多核系统的任务调度问题已经成为本领域内最重要的研究方向。多核系统主要由计算资源和通信资源组成,多核系统的调度问题可以概括为多计算资源和通信资源在时间轴上的分配问题。优秀的资源调度算法能合理地分配多核系统计算资源,有效降低处理器计算的总执行时间和总耗费量,从而尽可能挖掘系统潜在性能。在超级计算机中,已经有很多相关问题的解决方案,例如,基于遗传算法和蚂蚁算法的启发式智能任务调度,源自于人工智能的Agent技术,严格定义的数学对象Petri网,以及多客户多服务器方式的各种任务调度算法。但是,以上提到的算法的应用大多是针对超级计算机的,对于微型的多核系统虽有其借鉴意义,但不能直接应用。而且,对于单个大任务的分解及调度、各子任务之间的联络通信等情况需特殊考虑。遗传算法利用简单的编码技术和繁殖机制来表现复杂的现象,从而解决非常困难的问题,其求解过程也可看作是最优化过程。将遗传算法应用于多核任务调度中,利用遗传算法所具有的并行性和全局解空间搜索的特点,实现合理的任务分配,以达到负载平衡的目的。这样可以有效地缩短任务的完成时间,提高多核系统资源的使用效率。
1 系统平台
此实验的系统平台如图1所示,为基于二维网格的NoC(Network on Chip)系统。选择这种结构的原因有:二维网格是主流的网络拓扑结构,利用IC平面工艺实现的方便性,XY路由策略的简易性以及网络的可测量性。在这种结构中,每个计算节点都与一个通信节点相连,网拓扑结构为二维网格,节点数目可以是2×2、3×3、4×4、M×M等。物理层采用同步握手协议,网络层采用XY路由算法。图1所示的系统平台示意图中,圆圈代表各处理器,各处理器之间的实线箭头代表各处理器之间的通信通道,虚线箭头为遗传算法的配置信号,点横线箭头为监控模块的监测信号。遗传算法模块搜寻可以并行的子任务,并将其合理地分配到相应计算节点中;监控模块监控各处理器的负载情况。此后的实验以其中两个核的任务分配为实验对象,验证所用遗传算法的优化作用。
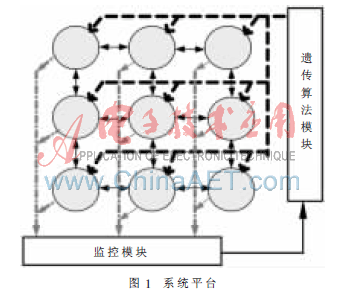
2 实验及应用
矩阵求逆算法过程:设矩阵A的各阶主子式|Aii|≠0(i=1,2,…,n),则可以对A分解为:A=L×U。其中L为主对角线元素全为1的下三角矩阵(即单位下三角矩阵),U为上三角矩阵。对于规模较大的矩阵,WANG K在1982年提出了块LU分解方法[7,8]。假设输入为一个n×n矩阵A=(aij),分解为k2个m×m子矩阵Aij,其中i、j=1,2,…,k;n=km。输出:k(k+1)个子矩阵Lpq,其中q≤p=1,2,…,k;子矩阵Urs,s≥r=1,2,…,k,每个子矩阵为m×m。对矩阵进行块LU分解后,也可以对三角矩阵进行分块求逆。其算法为,先对主对角线上的分块子矩阵求逆,再对与主对角线平行的各斜列上的子矩阵进行相应的操作。由于A=L×U,因此A-1=U-1×L-1,为了提高算法并行度,同样可以使用块矩阵乘法计算。把块U-1与L-1相乘,就可以得到所求矩阵的逆。
根据上述的算法过程,可将算法整体分为三大步骤:分块LU分解、三角矩阵分块求逆和矩阵分块相乘。虽然在同一个块矩阵中这三步是依次进行的,但是各矩阵块的运算并不是互为前提的,所以有些步骤的运算可以并行进行。而合适的遗传算法可以通过搜索寻找到这些可以并行的子任务,并将其合理地分配到相应计算节点中,从而减少系统运算时间,提高系统资源利用率。
遗传算法执行过程:参照参考文献[1-4],调整算法底层函数的实现方法和底层函数调用顺序,使之适合本文的目标任务。算法执行过程如下:
(1)分解:将目标任务——5×5的矩阵块(每个矩阵块为3×3维的矩阵)的LU分解求逆分解成72个子任务;
(2)高度函数[1]:为了促进调度的产生和遗传算子的构造,定义任务图中每个任务的高度为:
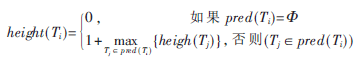
(3)分组:依据各子任务的高度值将其分为两组,并在此基础上调用底层函数Generate_Schedule,生成初始种群;
(4)适应度:计算每个个体的适应度值(运算时间越短,适应度值越大);
(5)繁殖:基于适应度值,在繁殖的执行过程中采用轮盘赌算法,产生新个体;
(6)交叉:在区间[1,max{height}]中产生随机数c,分别交换两个体中高度值大于c的部分,一组新个体便产生了;
(7)选择:比较交叉前后两个体的适应度值,选择较好的一组并将其储存在新群体中;
(8)循环:循环执行步骤(4)~(7) maxgen次(maxgen的值已预设);
(9)找出最终调度循序:在最终的群体中,选择适应度值最大的个体即为所求。
遗传算法顶层调度模块:
T=task_graph;
%-------------初始化--------------
gen=0; %代计数器
maxgen=5; %最大遗传代数
m=1;
N=30; %调用函数Generate_Schedule次数---pop_size
for i=1:N
[P_T,height]=Generate_Schedule(T);
POP(i)={P_T};
end
%-----------循环迭代---------------
while(gen<maxgen)
for i=1:N
[fitness_value(i),T_delt]=Fitness(POP{i},T);
end
New_pop = Reproduction(POP,fitness_value);
for i=1:size(New_pop,2) %对New_pop里的每个
string调用函数crossover,产生新的个体
P_T_new=Crossover(cell2mat(New_pop(i)),height);
for m=1:size(P_T_new,1)
for n=1:size(P_T_new,2)
if(P_T_new(m,n).name==0)
P_T_new(m,n).name=[];
end
end
end
if(Fitness(P_T_new,T) > Fitness(cell2mat(New_pop
(i)),T))
POP(i)={P_T_new};
else
POP(i)=New_pop(i);
end
end
gen=gen+1;
end
%在最终的群里中挑选fitness_value最大的一个个体,即为所求
for i=1:size(POP,2)
fitness_value2(i)=Fitness(POP{i},T);
end
for i=1:length(fitness_value2)
if(fitness_value2(i)==max(fitness_value2))
T_best=POP(i); %T_best即为所求
min_time=1/fitness_value2(i);
end
end
将优化调度过的八核处理器的处理耗时与手动调度的处理耗时进行比较,如表1所示。为了使试验更加具有针对性,在此假设核之间的通信耗时为零,核之间通信速度对实验结果的影响将在以后的研究中予以深入分析。

手动调度的任务分配如下:前三个块矩阵的求逆运算放在第一个核中进行,第四、五两个矩阵块的求逆运算放在第二个核中进行。
实验结果表明,与之前的手动的分解调度相比,应用此遗传算法后计算速度明显加快,且随着族群数量和遗传代数的增加,优化程度增高。
本文针对已有的微型多核系统,以遗传算法为研究手段,以多任务到多核系统的映射过程为研究核心,实现了系统资源的优化分配,有效地缩短任务的完成时间,提高多核系统资源的使用效率;提高了多核系统的并行计算能力,减少了任务的平均响应时间;提高了多核系统吞吐量和系统的资源利用率。
由于遗传算法本身的局限性,不可能找到最优解,但算法可以进一步改进,例如增加新的算子[2],增大最优个体产生的几率,或改进现有的遗传算法[5-6];改进任务调度方案,增加其实时性,即在给各个处理器分配任务时,一旦某个处理器空闲,马上调用当前可以处理的子任务,而不用等到全部处理器处理完当前任务后同时启动下一组任务;增加计算节点数目,并在此基础上增加更多的优化目标[7]。
参考文献
[1] EDWIN S H,NINVAN A,Hong Ren.A genetic algorithm for multiprocessor scheduling[J].IEEE Transactions On Parallel And Distributed Systems,1994,5(2):113-114.
[2] TSUJIMURA Y,GEN M.Genetic algorithms for solving multiprocessor scheduling problems[M].Simulated Evolution and Learning, Springer-Verlag, Heidelberg,1997:106-115.
[3] ALBERT Y,ZOMAYA,YEE H.Observations on using genetic algorithms for dynamic load-balancing[J].IEEE Transactions On Parallel And Distributed Systems,2001,12(9).
[4] SRINIVASA P,MUSICUS B R.Generalized multiprocessor scheduling and applications to matrix computations[J]. FIEEE Transactions on Parallel and Distributed systems,1996,7(6).
[5] WU A S,Han Yu,Jin Shiyuan,et al.An incremental genetic algorithm approach to multiprocessor scheduling[J]. IEEE Transactions On Parallel And Distributed Systems, 2004,15(9).
[6] MOHAMMAD R B,MOHSEN E M.A bipartite genetic algorithm for multi-processor task scheduling[J].Int J Parallel Prog, 2009(37): 463-465.
[7] RAMANUJAM N,KALYANARAMAN K,NAGAPPAN M, et al.Dynamic task scheduling using parallel genetic algorithms for heterogeneous distributed computing[C].Proceedings of the 2006 International Conference on Grid Computing & Applications(GCA),Las Vegas, Nevada, USA, June 26-29, 2006.

